Application of a New Method of Nonlinear Dynamical System Identification to Biochemical Problems
A. V. Karnaukhov* and E. V. Karnaukhova
Institute of Cell Biophysics, Russian Academy of Sciences, Institutskaya ul. 3, Pushchino, Moscow Region, 142290 Russia; E-mail: akarn@icb.psn.ru* To whom correspondence should be addressed.
Received July 26, 2002; Revision received November 22, 2002
The system identification method for a variety of nonlinear dynamic models is elaborated. The problem of identification of an original nonlinear model presented as a system of ordinary differential equations in the Cauchy explicit form with a polynomial right part reduces to the solution of the system of linear equations for the constants of the dynamical model. In other words, to construct an integral model of the complex system (phenomenon), it is enough to collect some data array characterizing the time-course of dynamical parameters of the system. Collection of such a data array has always been a problem. However difficulties emerging are, as a rule, not principal and may be overcome almost without exception. The potentialities of the method under discussion are demonstrated by the example of the test problem of multiparametric nonlinear oscillator identification. The identification method proposed may be applied to the study of different biological systems and in particular the enzyme kinetics of complex biochemical reactions.
KEY WORDS: identification method, nonlinear dynamical model, enzyme kinetics, biochemical reaction cascade, ordinary differential equation system in Cauchy explicit form, graphic method, Prony's method, asymptotic method
When studying biological subjects such as an entire organism, individual living cell, or isolated biochemical reaction, we deal with complex systems. The conventional scheme of construction of integral models of complex systems involves the following stages: 1) extraction of simple subsystems (processes) in the system (phenomenon) under study; 2) experimental establishment of the functional relationships between the separate subsystems in studies of fragments of the original system; 3) “assembly” of the integral model, the use of numerical and analytical methods of simulation modeling for checking the completeness and adequacy of the relationships established at the second stage.
It should be noted that this scheme is operative only in the cases when the fragments of the original system can be experimentally isolated with no irreversible change of their properties. However such a possibility is not consistently realized. For example, deviations from the hyperbolic law are observed in studies of the dependence of the enzymatic reaction rate on the substrate concentration [1]. The kinetic anomalies may be due to the complicated mechanism of the enzymatic process: nonequivalence of the substrate-binding sites or interactions between the substrate-binding sites in the molecule of oligomeric enzyme or heterogeneity of the enzyme preparation when the latter contains forms (including oligomeric forms) differing in the catalytic properties [2]. Besides, many biochemical reactions proceed with the formation of a broad spectrum of intermediates.
Choosing between the mechanisms proposed for explanation of the observed kinetic anomalies is often a challenging task. Therefore, empiric equations proposed for description of the kinetics of enzymatic reactions remain popular among enzymologists [3, 4]. Thus, even when studying separate enzymatic reactions, explorers run into a non-trivial problem in isolation of simple subsystems. As for the cascades of biochemical reactions accompanying, for example, apoptosis [5] or blood coagulation [6], the problem here is worse.
In the present paper we have elaborated a new method of identification of the systems. This method allows us to construct the mathematical models of complex (multiparametric) nonlinear phenomena, i.e., the phenomena typical of biological systems, without experimentally exploring separate fragments of the original system.
System identification is a relatively new line of theoretical investigations evolved at the interfaces between mathematics, physics, and cybernetics (control theory). A set of methods used for system identification is very wide, namely from the simplest statistical and spectral methods to the methods of identification of multiparametric nonlinear dynamic systems.
It should be noted that system identification as a line of scientific investigations was developed under the influence of the problems of technical system control. However some methods of system identification became useful for experimenters. A number of the methods of system identification are widely used by biochemists for analysis of the kinetics of enzymatic reactions, the most-used methods being the graphic method ([7], pp. 695-699) and Prony's method [8]. In short we can say that these methods and other methods applied for the study of the kinetics of the enzymatic reactions ([7], pp. 372-375) allow only linear or asymptotically linear systems to be analyzed. However, most enzymatic reactions are described by systems of nonlinear differential equations. Therefore, the experimenter should choose the conditions of the experiment so that the system is linearized (for example, by using high concentrations of one of the reactants) or study reactions differing greatly in the rates. In the last case (according to the Tikhonov theorem ([7], pp. 707-708) the number of degrees of freedom of the system to be identified can be reduced.
Many specialists in the field of system identification believe that “nonlinear problem of prediction (identification) has no finite-dimensional solutions with the exception of particular cases” [9]; it is thought that analytical solutions are lacking. Using the numerical methods for nonlinear problem is confined by the technical potentialities of computers. Therefore, planning of experiments includes only models with a small number of parameters.
The method elaborated in the present paper allows the solution of identification problem in an analytical form to be obtained for a variety of nonlinear systems. The problem is reduced to the solution of a system of linear equations [10, 11]. It should be noted that there are quick numerical algorithms for solution of the system of linear equations.
Experiments in studies of the kinetics of the enzymatic reactions are carried out, as a rule, with regard to the corresponding methods of treatment of the results of measurements. Therefore, the method of system identification proposed by us allows a new class of experiments with a great number of reactants to be designed. One can expect that the application of this method will permit the range of the biochemical problems accessible to investigation to be expanded and a higher accuracy of determination of the kinetic parameters for complex biochemical reactions to be obtained.
STATEMENT OF THE IDENTIFICATION METHOD
Consider the class of nonlinear dynamic models represented by the system of differential equations in the Cauchy explicit form with a quadratic right part:
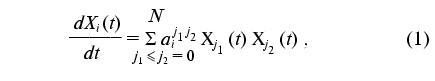
where Xi(t) is a set of dynamic parameters of the phenomenon under study (i = 0, ..., N), aij1j2 are the constants of the dynamic model (j1 <= j2 = 0, ..., N).
It should be noted that the addition of the formal parameter X0(t) = 1 to the set of dynamic parameters Xi(t) in model (1) allows us to pass on to the Cauchy system with the quadratically linear right part. Equality aij1j2 = 0 provides a consistency of the (N + 1)-dimensional model with additional formal parameter X0(t) = 1. Introduction of an additional formal parameter is a convenient technique that allows the form of the original model to be simplified and standardized. Such a technique can be useful also for generalization of the identification method under discussion to the cases of models represented by a system of differential equations in Cauchy form with arbitrary polynomial right part.
The class of the quadratic (quadratically linear) models is only a particular case of the more general class of polynomial models, the latter in turn are a particular case of nonlinear models with arbitrary piecewise continuous right part. Nevertheless, it is possible to describe a broad spectrum of phenomena in nonlinear systems in the frames of quadratic (quadratically linear) models.
When discussing biochemical problems, we should take into account that monomolecular chemical reactions (first-order reactions) are described by linear terms, whereas quadratic terms are introduced for description of bimolecular reactions (second-order reactions). It should be noted that “reactions of the third order (trimolecular reactions) are extremely rare in occurrence” ([7], p. 21). Therefore, the quadratic model (1) may be thought of describing the general case of the cascade of simple biochemical reactions. Moreover, since any complex reaction is eventually a set of simple reactions, the general case of a cascade of complex biochemical reactions may be also described in the frames of model (1).
In contrast to the direct problem of modeling, the problem of identification (or the inverse problem of modeling) is the determination of the constants of the dynamic model aij1j2 on the basis of the known time-dependences of dynamic parameters Xi(t).
The set of the constants of the dynamic model aij1j2 is determined from the condition of minimization of quadratic discrepancy functional for the concrete realization of the time-dependence of the dynamic parameter set of the phenomenon under study Xi(t):
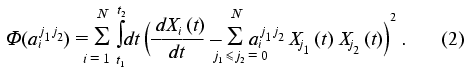
It is easy to show (see “Appendix”) that the constants of the dynamic model aij1j2 providing the minimum of functional (2) can be calculated as follows:
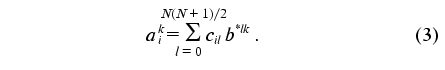
Here aik =
aij1j2
is a desired set of constants of the dynamic model,
b*lk are the elements of matrix, which is
inverse with respect to matrix {bml}. According to
the definition
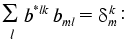
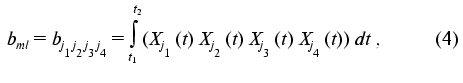
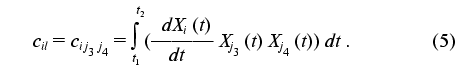
The transition from indices j1, j2, j3, j4 to indices k, l, m is a procedure of renumbering indexed variables in accordance with the algorithm of direct product of multitudes (see “Appendix”, item 2). This allows the system of linear equations to be written and solved using standard program packages (for example, MATLAB 6.1).
As can be seen, the problem of identification of the original nonlinear model (1) in the frames of the criterion of quadratic discrepancy minimization (2) has a simple analytical solution (3)-(5).
In the case of biochemical problems the constants of the dynamic model aij1j2 can be interpreted as the constants of the biochemical reactions. Dynamic parameters of the phenomenon under study Xi(t) are concentrations of reactants including the concentrations of intermediates.
Thus, to construct the integral model (1) of the complex system (phenomenon), it is necessary to obtain some data array (to a sufficient degree of specification) characterizing the time-dependent change in parameters Xi(t) of the system (phenomenon). Obtaining such a data array has always been a problem. However, difficulties emerging are preferentially of a technical character and can be almost without exception surmounted.
Consider in more detail the application of the method proposed by us to the description of a concrete biochemical reaction, namely the ligand-receptor interaction. Since the description of the model of the simple receptor binding presents no special problems ([7], p. 342), it is of interest to discuss more complex ligand-receptor interaction taking into account the processes of degradation of ligands (degradation by enzymes) and internalization (exocytosis) of receptors, ligands, and ligand-receptor complexes. The changes in the concentration of ligands and receptors may be presented by the following scheme [12]:
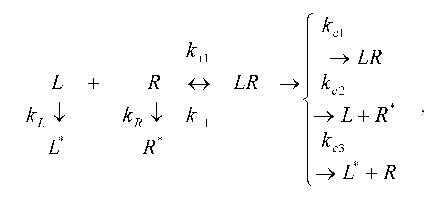
where L is ligand, R is receptor, LR is the complex of ligand with receptor, and k+1 and k-1 are the rate constants for the formation and breakdown of the ligand-receptor complexes. The products of degradation or internalization of the corresponding component are designated by an asterisk. The scheme includes the following stages: degradation of the ligand (with the rate constant kL), internalization of free receptors (kR), internalization of the ligand-receptor complexes (kc1), internalization of the receptor (kc2), and internalization of the ligand from the ligand-receptor complexes (kc3).
The law of conservation of matter is written as follows:
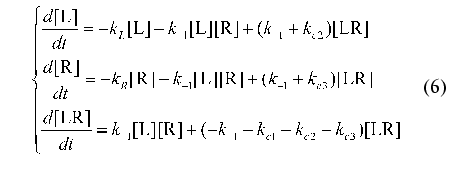
It should be noted that the similar system of differential equations has no analytical solution. However the system allows the investigations to be carried on in the frames of the proposed method of identification. For this purpose consider in more detail the transition to universal designations used in the present paper.
The following designations are used:
To describe the linear terms, the additional variable X0(t) = 1 is introduced. The system of equations (6) acquires the following form:
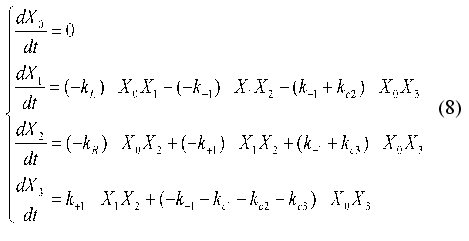
The matrix of the constants of the dynamic model {aij1j2}(j1 <= j2 = 0, ..., 4) where index i corresponds to the number of equation in the system of equations (4), j1 are matrix rows, and j2 are matrix columns is written as follows:
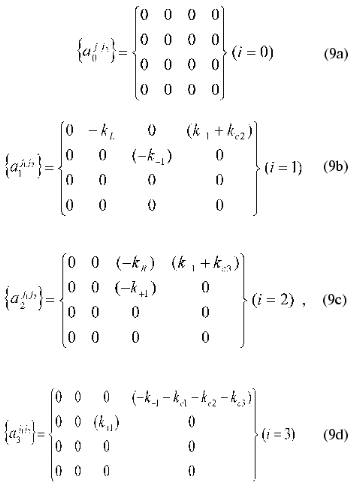
It should be noted that a triangular shape of matrix (9) (aij1j2 = 0 at j1 > j2) allows ambiguity in determination of the matrix coefficients to be avoided.
Thus, with the designations (7)-(9) the system of equations (6) can be put in form (1) at N = 3. When the time-dependent changes in the concentrations of reactants are known, substitution of the corresponding values into expressions (4) and (5) allows the numerical values of the matrix coefficients aij1j2 to be obtained. The latter may be used for determination of the rate constants for the concrete chemical reactions: kL, kR, k+1, k-1, kc1, kc2, kc3.
TEST PROBLEM OF IDENTIFICATION OF MULTIPARAMETRIC NONLINEAR
OSCILLATOR
Consider the application of method under discussion by the example of the test problem of identification of nonlinear oscillator with three degrees of freedom:
N-dimensional quadratically linear model (N = 3)
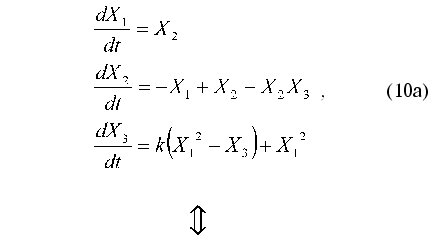
(N + 1)-dimensional quadratic model (N = 3)
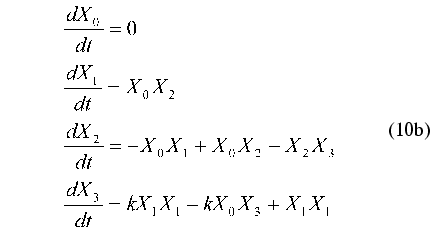
As noted above, parameter X0(t) = 1 is introduced to put the right part of Eq. (10b) in form (1). Therefore, this parameter cannot be considered as an additional degree of freedom.
It is easy to show that at k --> infinity the systems of equations (10a) and (10b) describe the standard Van der Pol oscillator.
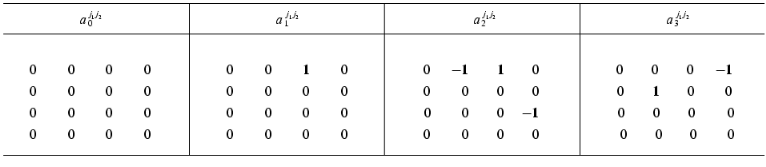
Table 1 gives the matrix of the constants of the dynamic model aij1j2 (at k = 1) for putting the equation system (10b) in the form of evolution equation (1) where index i corresponds to the number of the equation and indices j1, j2 correspond to the numbers of dynamic parameters Xi(t).
Table 1. The exact values of the constant
matrix of the dynamic model
{aij1j2}
for the system of equations (10b) (i is the number of the
equation, j1 are the matrix rows,
j2 are the matrix columns)
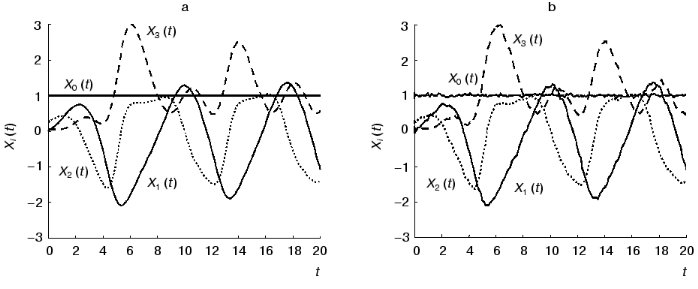
The testing of the method is conducting in several steps. In the first step we obtain the solutions of the system (10b) over some time interval (from 0 to 20) using Runge-Kutta method (altogether P = 157 values) and consider them as dynamic parameters of the system under study Xi(t) (figure, panel (a)).
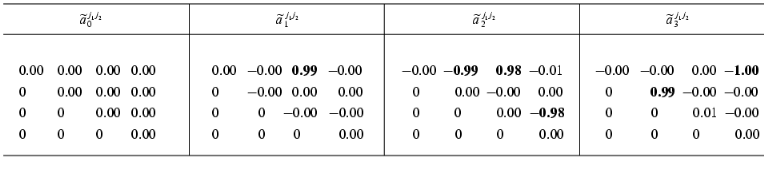
In the second step we consider the constants of the dynamic model aij1j2 as unknown magnitudes and try to reconstruct their values in accordance with formulae (3)-(5). Designate the reconstructed values as ~aij1j2. We compare the ~aij1j2 values obtained by the identification method under discussion (Table 2) with the exact values aij1j2 (Table 1). As can be seen, the agreement is very good: the error does not exceed 2%.Time-dependence of the dynamic parameters Xi(t) (i = 0, ..., 3) obtained by the solution of the system of equations (10b) at k = 1 in the absence of the noise component (a) and with noise S = 0.06 (b)
Table 2. Reconstructed values of the
constant matrix of the dynamic model
{~aij1j2}
(the noise amplitude S = 0, the number of the experimental
values Xi(tp): P = 157)
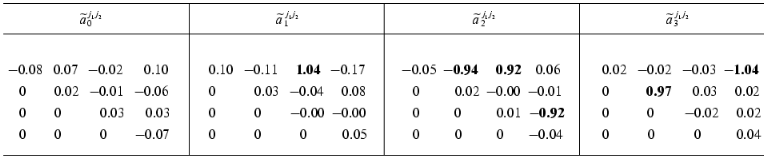
Consider the application of the method in circumstances where we must reckon with noise. Table 3 shows the reconstructed ~aij1j2 values for the model with the noise component having the amplitude of S = 0.06 (figure, panel (b)). When the numerical experiment was carried out, the noise component was added not only to dynamic parameters of the system Xi(t) (i != 0), but also to the formal parameter X0(t). By its variation from zero ~aij1j2 serve as a characteristic of measuring inaccuracy. The values of the constants of the dynamic model were obtained with a sufficiently high accuracy. In spite of high level of noise, the average error in determining the ~aij1j2 values does not exceed 10%. The accuracy in determining the matrix elements {~aij1j2} rises as the number of the experimental points P increases.
Table 3. Reconstructed values of the
constant matrix of the dynamic model
{~aij1j2}
(the noise amplitude S = 0.06, the number of the experimental
values Xi(tp): P = 157)
The method of system identification proposed in the present paper may be easily generalized to a broader class of nonlinear models described by the system of differential equations in the Cauchy form with arbitrary piecewise continuous nonlinear right part (not necessarily quadratic or polynomial).
Further development of the method is connected with application of its concrete modifications for a broad class of special problems of biology and medicine, in particular biochemical problems, which are now solved by the standard methods using exponential models and asymptotic approximations (for example, graphic method and Prony's method). The advantage of the method is to allow substantially more complex reactions to be studied.
An important feature of the method is its applicability to analysis of biochemical systems not possessing an asymptotic behavior. As indicated above by the example of identification of parameters for the of oscillator of the Van der Pol type, the method may be successfully applied for description of the behavior of stochastic models and self-oscillating systems, such as the well-known Belousov-Zhabotinsky reaction [13] or phenomenon of oscillations of receptor binding ([7], pp. 491-495).
The method is of importance for developing the quantitative models of aging, pathological processes, and systemic diseases accompanying aging and also for elaborating the optimal programs of therapy taking into account the individual peculiarities of a patient.
Recent technical achievements in carrying out biochemical experiments open up new fields of the application of the method under discussion. In particular, EPR- and NMR-spectrometry provide continuous recording of the time-depended changes in the concentrations of a large number of reactants and intermediates.
The authors are ready to cooperate and can provide a useful guide to set up a problem as well as to analyze the data obtained.
APPENDIX
1. The set of the constants of the dynamic model aij1j2 is determined from the condition of minimum of quadratic discrepancy functional Phi(aij1j2)
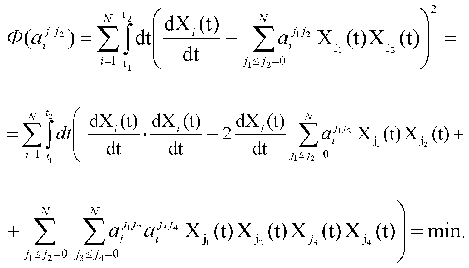
and essentially corresponds to the “best” description of the experimentally measured dynamic parameters of the system Xi(t) in the frames of the standard criterion of the least-squares method. To obtain the concrete expression for Phi(aij1j2), we can use the condition of the extremum (minimum) of functional, i.e., equality to zero for the partial derivatives of functional Phi(aij1j2) with respect to variable parameters aij1j2:
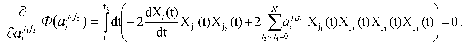
Changing the order of integration and summation, we get the following expression:
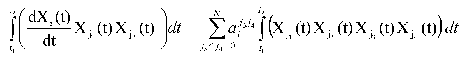
Introduce the following designations:
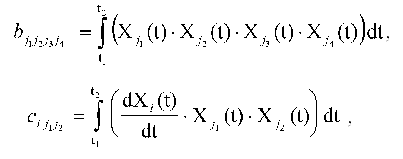
where i = 0, ..., N; j1 <= j2 = 0, ..., N; j3 <= j4 = 0, ..., N. The expression for the constants of the dynamic model aij1j2 providing the extremum of quadratic discrepancy may be written in the form:
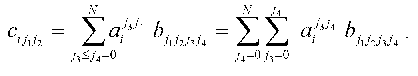
To put expression obtained in the standard form of the system of linear equations, the elements of the arrays should be renumbered in accordance with the algorithm of direct product of multitudes (see below): bkl = bj1j2j3j4, cik = cij1j2, and (k <--> j1 (x) j2; l <--> j3 (x) j4; j1 <= j2; j3 <= j4):
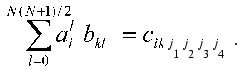
Thus, we get aggregate of N systems of linear equations (index i). Each of the systems is a system of linear equations of rank N(N + 1)/2 for ail. The solution has the standard form:
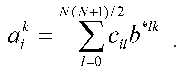
Here b*lk are the elements of the matrix, which is inverse to matrix {bml}, or, by definition:
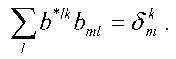
The aij1j2 values may be finally reconstructed by application of a renumbering procedure, which is inverse to the procedure used above for renumbering the elements of the arrays bkl = bj1j2j3j4, cik = cij1j2, and (k <--> j1 (x) j2; l <--> j3 (x) j4; j1 <= j2; j3 <= j4), to ail values obtained.
2. Operation (x), for example, (k <--> j1 (x) j2; j1 <= j2), is a procedure of the renumbering of the elements of the array in accordance with the algorithm of the direct product of multitudes. Consider, for example, the two-dimensional array aij1j2 and corresponding one-dimensional array ak where to every element of the two-dimensional array aij1j2 (j1 <= j2) corresponds one element of the one-dimensional array ak, and one element only. Such a correspondence specifies the display where to every pair of the values of the indices j1, j2 (j1 <= j2) corresponds one value of the index k, and one value only. It should be noted that the different concrete realizations of such a display can be used. One of the possible realizations is the following:
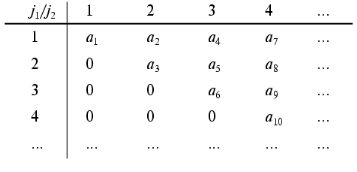
It should be noted that the condition j1 <= j2 is necessary for avoiding ambiguity in evaluating the constants of the dynamic model aij1j2.
REFERENCES
1.Hill, C. M., Waight, R., and Bardsley, W. G. (1977)
Mol. Cell. Biochem., 15, 173-178.
2.Kurganov, B. I. (1982) Allosteric Enzymes.
Kinetic Behaviour, J. Wiley and Sons, Chichester, pp. 32-54.
3.Ainsworth, S. (1977) J. Theor. Biol.,
68, 391-413.
4.Kurganov, B. I. (2000) Biochemistry
(Moscow), 65, 898-909.
5.Samuilov, V. D., Oleskin, A. V., and Lagunova, E.
M. (2000) Biochemistry (Moscow), 65, 873-887.
6.Jesty, J., Wun, T. C., and Lorenz, A. (1994)
Biochemistry, 33, 12686-12694.
7.Varfolomeev, S. D., and Gurevich, K. G. (1999)
Biokinetics. Apprentice Course [in Russian], FAIR-PRESS,
Moscow.
8.Marple, S. L. (1987) Digital Spectral Analysis
with Applications, Prentice-Hall.
9.Ljung, L. (1999) System Identification. Theory
for the User, 2nd ed., PTR Prentice Hall.
10.Karnaukhov, A. V., and Karnaukhova, E. V. (1999)
Methods of System Identification in Physiology and Medicine.
Proc. Int. Sci.-Practical Conf. “Measuring Informational
Technologies and Instrumentation in Health Protection”, St.
Petersburg.
11.Karnaukhov, A. V., and Karnaukhova, E. V. (2000)
Methods of System Identification in Biology and Medicine.
Proc. of School-Conference “Horizons of Physico-Chemical
Biology”, Pushchino.
12.Ariens, E. J., Beld, A. J., Rodrogies de Mirande,
J. F., and Simonis, A. M. (1979) in The Receptors: a Comprehensive
Treatise, Vol. 1, New York, pp. 33-91.
13.Zhabotinsky, A. M. (1974) Concentration
Waves [in Russian], Nauka, Moscow.