REVIEW: Reflections on Biocatalysis Involving Phosphorus*
G. M. Blackburn1**, M. W. Bowler2, Yi Jin1, and J. P. Waltho1,3
1Krebs Institute, Department of Molecular Biology and Biotechnology, University of Sheffield, Sheffield S10 2TN, UK; E-mail: g.m.blackburn@shef.ac.uk2Synchrotron Science Group, European Molecular Biology Laboratory, BP 181, 6 rue Jules Horowitz, 38042 Grenoble Cedex 9, France
3Manchester Interdisciplinary Biocentre, Manchester, M1 7DN, UK; fax: +44-114-222-2800
* This review is based on the Arbusov Medal Award Lecture of Professor G. M. Blackburn at the Butlerov Conference in Kazan, October 2011.
** To whom correspondence should be addressed.
Received May 1, 2012
Early studies on chemical synthesis of biological molecules can be seen to progress to preparation and biological evaluation of phosphonates as analogues of biological phosphates, with emphasis on their isosteric and isopolar character. Work with such mimics progressed into structural studies with a range of nucleotide-utilising enzymes. The arrival of metal fluorides as analogues of the phosphoryl group, PO3–, for transition state (TS) analysis of enzyme reactions stimulated the symbiotic deployment of 19F NMR and protein crystallography. Characteristics of enzyme transition state analogues are reviewed for a range of reactions. From the available MFx species, trifluoroberyllate gives tetrahedral mimics of ground states (GS) in which phosphate is linked to carboxylate and phosphate oxyanions. Tetrafluoroaluminate is widely employed as a TS mimic, but it necessarily imposes octahedral geometry on the assembled complexes, whereas phosphoryl transfer involves trigonal bipyramidal (tbp) geometry. Trifluoromagnesate (MgF3–) provides the near-ideal solution, delivering tbp geometry and correct anionic charge. Some of the forty reported tbp structures assigned as having AlF30 cores have been redefined as trifluoromagnesate complexes. Transition state analogues for a range of kinases, mutases, and phosphatases provide a detailed description of mechanism for phosphoryl group transfer, supporting the concept of charge balance in their TS and of concerted-associative pathways for biocatalysis. Above all, superposition of GS and TS structures reveals that in associative phosphoryl transfer, the phosphorus atom migrates through a triangle of three, near-stationary, equatorial oxygens. The extension of these studies to near attack conformers further illuminates enzyme catalysis of phosphoryl transfer.
KEY WORDS: phosphate esters, nucleotide analogues, α-fluorophosphonates, kinases, mutases, metal fluorides, transition state analogues, NACsDOI: 10.1134/S000629791210001X
ENCOUNTER WITH BIOLOGICAL PHOSPHATE CHEMISTRY
Alexander Robertus Todd was awarded the Nobel Prize for Chemistry and Physics in 1957 for his work on nucleotides and nucleotide coenzymes. His new laboratory in Cambridge, where General Secretary Khrushchev made a site-visit in 1955, was a world centre for natural product chemistry that by 1959 had become focused on the synthesis of Vitamin B12, nucleic acids, and natural products. He assigned Jack S. Cohen the task of the synthesis of oligonucleotides under the direction of one of the authors (GMB) and set them the task of exploring the polymerisation of 2′-deoxynucleotides by ring opening of their 3′,5′-cyclic phosphate esters. The well-known stability of 6-membered cyclic phosphates for both di- and tri-esters directed the focus to P(III) chemistry, and Cohen attempted the oligomerisation of 3′,5′-cyclic phosphite triesters, with subsequent oxidisation to phosphates and removal of the third ester group by acid or by hydrogenolysis. Because of the formidable cost of 2′-deoxynucleosides at that time, the work largely used simple bicyclic model triesters, aimed at the base-catalysis of transesterification. Only methyl cis-cyclohexane-1,3-diol cyclic phosphite showed any signs of polymerisation, and its oxidation product proved intractable. The positive outcome of the work was an early 31P NMR analysis of the dependence of chemical shift on structure that showed a characteristic 20-ppm downfield shift for 5-membered cyclic phosphates relative to 6-membered and acyclic phosphates [1].
A visit to Cambridge by Bruce Merrifield in early 1964 to describe his work on the solid-phase synthesis of oligopeptides persuaded Mike Blackburn that this was the right way to tackle the stepwise synthesis of oligonucleotides. That route was launched with Mike Harris and Mike Brown, a troika of Mikes, initially in Cambridge and then in Sheffield. While the synthesis of a tetramer of deoxythymidylic acid was soon achieved [2], the polystyrene polymers, prepared in-house, proved intractable to further chain extension and, in the face of the successes of the groups of Gobind Khorana and Robert Letsinger in the USA, the enterprise was abandoned in favour of an exploration of the photochemistry of nucleic acids. However, in a further application of solid-phase support chemistry, a novel use of the polystyrene matrix allowed the analysis of the mechanism of dicyclohexylcarbodiimide (DCCI) mediated condensation of phosphate mono-esters with alcohols. This condensing agent was the widely-accepted means of synthesising phosphate diesters, invented by Gobind Khorana, which dominated oligonucleotide synthesis for a decade. The mechanism of the reaction did not follow the metaphosphate process preferred by Todd but involved condensed phosphate systems, best described as cyclic trimetaphosphates [3].
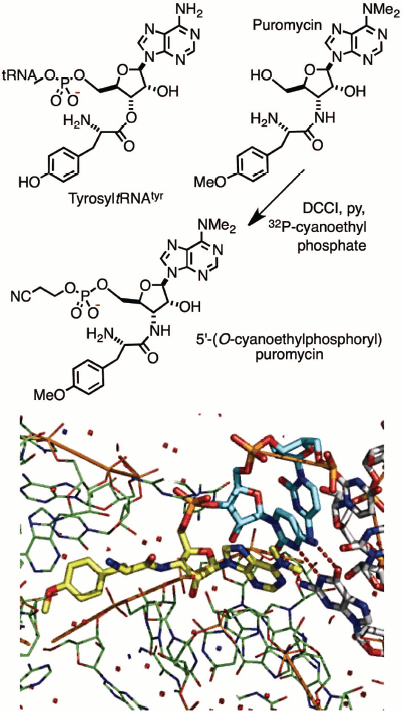
A group of Cambridge chemists working on nucleic acids held joint meetings with molecular biologists in Francis Crick’s MRC laboratory and led to a collaborative investigation of the mechanism of protein biosynthesis. Puromycin was a known inhibitor, believed to block the ribosome by its mimicry of tyrosyl-tRNATyr. This study called for production of an isotopically-labelled derivative of the antibiotic of extremely high specific radioactivity. It led to the synthesis of 32P-labelled puromycin by using DCCI with 20 mCi (740 MBq) of carrier-free 2-cyanoethyl [32P]-phosphate. This derivative (Fig. 1; see colour insert) did indeed bind to the ribosome, inhibiting peptide elongation, and thereby established the translocation mechanism between the aminoacyl (A) and peptidyl (P) tRNA sites on the ribosome. It was one of the earliest contributions to the chemical biology of phosphates [4]. It is rewarding to see the subsequent validation of that work by Tom Steitz in an X-ray structure of puromycin bound to two cytidines in the A-site of the 50S ribosome (Fig. 1, Protein Data Bank (PDB) entry 1Q82) [5].
Fig. 1. Synthesis (upper) of puromycin 5′-(2-cyanoethyl phosphate) and (lower) structure of 50S ribosome with puromycin 5′-phosphate (yellow) linked to 3′-cytidylylcytidine (cyan) bound in the A-site of the 50S ribosome (green) [5].
PHOSPHONATES AS MECHANISTIC PROBES AND ENZYME LIGANDS
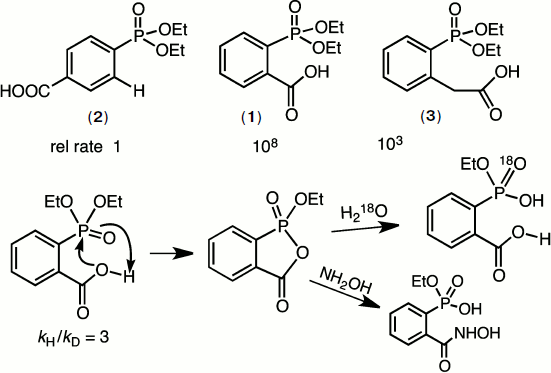
In 1966, GMB took sabbatical leave in the laboratory of William P. Jencks and developed a strong interest in catalysis of ester aminolysis and phosphate ester hydrolysis aimed at biocatalysis. A particular problem at that time was the remarkable intramolecular catalysis of the hydrolysis of diethyl 2-carboxyphenylphosphonate (1) relative to that of diethyl phenylphosphonate (2). Mike Brown solved the mechanism by a combination of kinetic, structural, and isotope studies. It proved to be the first demonstration of the powerful nucleophilic reactivity of the carboxyl function towards phosphate esters, a rate acceleration of 108 (Fig. 2) [6].
Such catalysis by a carboxylic acid group is now recognised as a key component of many phosphoryl transfer enzymes including mutases and phosphatases. The key features of the reaction are shown in Fig. 2. What is especially noteworthy is the requirement for accurate “in-line” attack of oxygen on the P=O group that is partially impeded in the case of the homologous ester (3). It predated the “orbital steering” hypothesis of Storm and Koshland [7] that appears now to have considerable relevance to enzyme catalysis of phosphoryl transfer [8].Fig. 2. Mechanism of hydrolysis of diethyl 2-carboxyphenylphosphonate (1). The addition of the carboxyl group to the phosphoryl ester generates a stable cyclic phosphonate ester that rapidly hydrolyzes to monoethyl 2-carboxyphenylphosphonate. This in turn cyclises to the phosphonic acid that finally ring opens to 2-carboxyphenylphosphonic acid. A kinetic isotope effect and the pH-rate profile of the reaction confirm that the carboxylic acid is active in its neutral form.
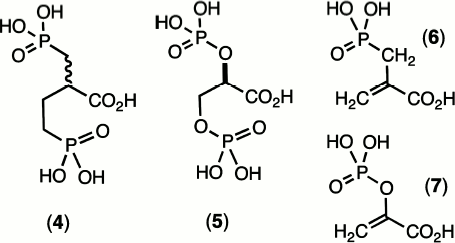
By contrast, the general stability of phosphonates and their anhydrides appeared to groom them for use as enzyme ligands to mimic labile phosphate esters and anhydrides. The early 1970s was a period when exploration of the mechanisms of catalysis of the glycolytic enzymes was a fast-expanding field, and X-ray protein structures were becoming more readily accessible. It was therefore timely to synthesise species such as 2-carboxybutane-1,4-bisphosphonic acid (4) as an analogue of 2,3-bisphospho-D-glyceric acid (5) and 2-carboxy-(prop-2-enyl)-phosphonic acid (6) as an analogue of phosphoenol pyruvate (7) (Scheme 1). Unexpectedly, the replacement of a P–O linkage by a P–CH2 moiety in a biological phosphate generally proved to be a modification that weakened the binding of these ligands to proteins. In particular, (4) binds to hemoglobin some 10× weaker than does (5). Even more disappointingly, (6) binds to pyruvate kinase some 100× weaker than the natural substrate (7) [9].
These effects encountered were quite general and other investigators experienced similar results, e.g. in Jeremy Knowles’ work on phosphoglycerate kinase (PGK) [10] and our own studies on phosphoglycerate mutase [11]. This disappointing behaviour of phosphonates as analogues of biological phosphates simply had to be attributed to the mismatch between the electronegativity of the bridging oxygen atom on phosphorus with the electropositive nature of the methylene group.
In fact, it is possible today to analyze an X-ray structure of hemoglobin complexed with D-glyceric acid 2,3-bisphosphate and see there are two key hydrogen bonds from Lys81 in each β-chain to the bridging oxygens of (5) whose deletion might well account for the ten-fold weakening in binding of the bismethylene analogue (4) [12]. In the same fashion, analysis of the X-ray structure of pyruvate kinase bound to ATP and oxalate (an isosteric analogue of pyruvate) reveals that Lys269 makes a key hydrogen bond to the oxygen lost in the analogue (6) [13]. This analysis clearly suggests that hydrogen bonding to an oxygen involved in bond breaking/bond making at phosphorus is more important than hydrogen bonding to passive oxygen(s) and is likely to be more important still in transition states for reaction (v.i.).
PHOSPHONATES AS ANALOGUES OF BIOLOGICAL PHOSPHATES
Up to 1980, the design of stable phosphonates as analogues of biological phosphates had focused on maintaining stereochemical comparability. Small molecule X-ray structures confirmed that there were only second order changes in bond lengths and bond angles on comparing methylenephosphonates with the prototype phosphate esters: isosteric quality was thus achieved. But more was needed! It was time for a new look at the challenge of generating improved phosphonates as analogues of biological phosphates.
A critical analysis of existing data on physicochemical properties of phosphonates, coupled to the stereochemical demands on apicophilicity for the now recognised “in-line” attack of oxygen nucleophiles on phosphates, led us to the theoretical concept of α-fluorophosphonates. These were to become isosteric and isopolar analogues of biological phosphates [14]. The problem was to combine stability of the group bridging the phosphoryl moiety to its organic host molecule along with appropriate electronegativity. This was theoretically accessible by introducing halogens, ideally fluorines because of their small size and powerful electronegativity, into the P–CH2 group [9, 14]. This structural modification in changing CH2 to CHF or CF2 was designed to resolve five “mismatch parameters”:
1) elevated pKa2 for a phosphonic acid versus corresponding phosphate monoester;
2) deshielding of phosphorus in 31P NMR of phosphonates, Δδ +28 ppm;
3) reduced P=O frequency in IR, –35 cm–1;
4) reduced apicophilicity for CH2 relative to O;
5) loss of hydrogen bond acceptance by CH2 with respect to O.
It was one thing to propose such a solution to the problem, it was quite a different matter to deliver it. Outside the pioneering work of Donald Burton in Iowa on the synthesis of fluoroarylphosphonates [15], little was known about the synthesis of α-fluoroalkane-phosphonates, and our team had to devise new procedures. At first these depended necessarily on dangerous or hazardous reagents such as perchloryl fluoride (FClO4) and diethylaminosulfur trifluoride (Et2NSF3). Happily, these have been superseded by more amenable reagents, in particular
SelectFluor©, N-fluorobisbenzene-sulfonimide. It is not necessary to describe here the synthetic achievements of our group and those of several other laboratories because that task has been very well reviewed recently by Vadim Romanenko and Valery Kukhar [16].
Progress in the synthesis of α-fluoro- and α,α-difluorophosphonate esters had necessarily to be backed up by an efficient means for converting them into phosphonic acids and their salts. The older methods of vigorous acid hydrolysis or hydrogenolysis were often unsuitable for preparing analogues of biological phosphates. Happily, the use of two reagents, iodotrimethylsilane in our hands [17] and bromotrimethylsilane by Charles McKenna [18], has become standard features of many syntheses. We note that both these reagents were, in fact, originally used in studies by Mikhail Grigorievich Voronkov [19] published in Russian.
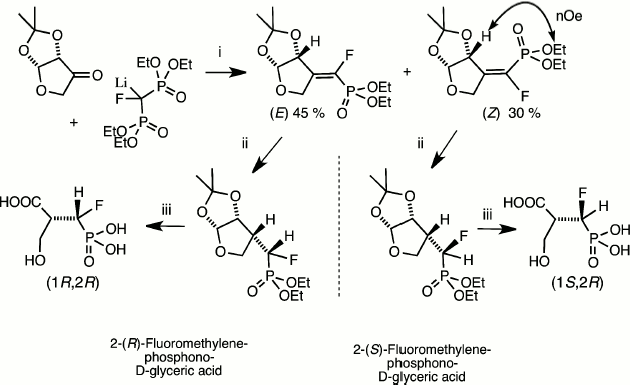
These key methods for phosphonate de-esterification enabled the synthetic use of catalytic reduction as a means of the stereospecific synthesis of homochiral α-fluoromethylenephosphonates. This was initially employed in our synthesis of discrete (R)- and (S)-isomers of the α-fluoromethylene analogues of 2-phospho-D-glyceric acid [20] and in an enantioselective synthesis of one isomer of the analogue of 3-phosphoglyceric acid [21] (Fig. 3). More recent routes to chiral α-fluorophosphonates as analogues of hexose phosphates and nucleotides have employed catalytic reduction in syntheses that depend on chiral separation of mixed diastereoisomers and their identification by NMR or X-ray analysis following hydrogenolysis of key functions [16, 22, 23].
Fig. 3. Synthesis of both chiral analogues of D-glyceric acid 2-phosphate [20]. Reagents (i) condensation then chromatographic separation and NMR identification of diastereoisomers; (ii) PdC/H2; (iii) Me3SiI then MeOH [17].
BIOCHEMICAL PERFORMANCE OF α-FLUOROPHOSPHONATES
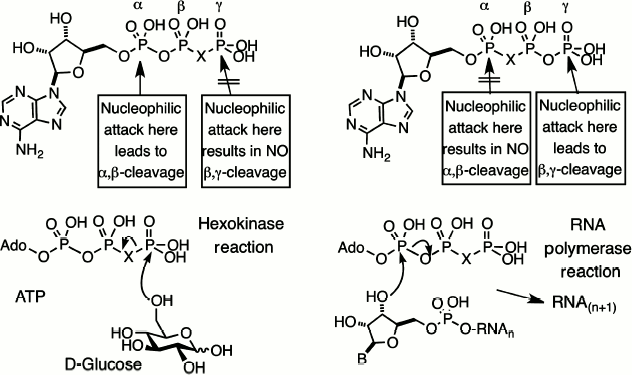
Substitution contiguous to the catalytic site of the substrate. Replacement of a bridging oxygen by a halomethylene function adjacent to the reacting phosphorus can lead to either modified substrate properties or total inhibition of reaction. This is well exemplified by the series of halomethylene analogues of nucleotides that we prepared in 1981, starting with ATP and GTP analogues [14, 25]. If the bridging carbon function is located in the β,γ-position, the nucleotide analogues will be substrates for enzymes that react at Pα but inhibitors for enzyme catalyzing reaction at Pγ or Pβ (Fig. 4, left).
By contrast, if the bridging carbon function is located in the α,β-position, the nucleotide analogues will be substrates for enzymes that react at Pγ but inhibitors for enzymes catalyzing reactions at Pα or Pβ (Fig. 4, right). The first example of dynamic enzyme studies with fluorophosphonate analogues was our use of a range of halomethylene analogues of ATP as substrates for hexokinase [26]. The order of reactivity of the bridging isosteric ligands was O > CF2 ≈ NH > CH2 > CCl2 with Vmax 10 : 4 : 4 : 2 : 1, respectively. One biosynthetic application of this satisfactory performance, in a collaboration with Bernard LeBleu, was our use of β,γ-difluoromethylene ATP as a substrate for 2,5-A polymerase, an RNA polymerase that makes oligoadenylic acids with the unusual 2′,5′-linkage, and delivered a stable analogue of the antiviral nucleotide, 2,5-A [27].Fig. 4. Halomethylene analogues of adenosine triphosphate. β,γ-Analogues and their pattern of enzyme cleavage or resistance as illustrated by hexokinase (left). α,β-Analogues and their pattern of enzyme cleavage or resistance as illustrated by ribonuclease (right).
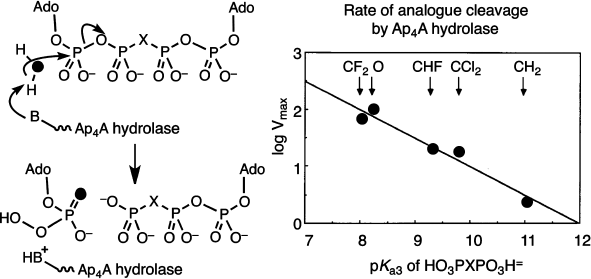
We next embarked on a mechanistic study of the enzymes that hydrolyze dinucleotidyl polyphosphates. Diadenosine 5′,5′′′-tetraphosphate, Ap4A, is a ubiquitous nucleotide that is regulated in all cells by specific hydrolases. The stereochemistry of α,β-hydrolysis of this nucleotide by a specific plant phosphodiesterase had been established as “in-line” by Gordon Lowe [28]. Hydrolysis of Ap4A in H218O gave AMP enriched in 18O from water attack at Pα. This showed us that it was opportune to measure the relative substrate kinetic rates of cleavage for a range of β,β′-halomethylene analogues of Ap4A as this modification must have a direct effect on the leaving group ability of the β,γ-halomethylene ATP product. The remarkable outcome of the kinetic analysis was a linear dependence of enzyme reaction rate on pKa4 of the bisphosphonate component of the ATP analogue over two decades of reactivity. The Brønsted slope β of –0.5 corresponds to a transition state with 50% breaking of the P–O bond, and that gave the first kinetic description of an associative process for an enzyme-catalyzed phosphoryl transfer mechanism (Fig. 5) [29].
More recently, Myron Goodman has completed a cognate study of the substrate activity of eight analogues of 2′-deoxyGTP by DNA polymerase beta [30]. These compounds give a Brønsted slope β of –0.59 for the C:G matched-pairing incorporation, though two parallel curves are needed to correlate the behaviour of the mono-halogen substituted compounds separate from the four bis-halogen substituted compounds. It is evident that adverse steric factors are influencing substrate binding for this enzyme, and the results will no doubt be re-examined after single stereoisomers of the three mono-halogen nucleotides become available.Fig. 5. Mechanism of cleavage of diadenosine 5′,5′′′-tetraphosphate (Ap4A) determined by the use of its β,β′-analogues. Pattern of incorporation of oxygen-18 from heavy water (left) and “in-line” attack. Brønsted plot of rates of enzyme catalyzed reaction as a function of pKa3 of the corresponding methylenebisphosphonic acids [29].
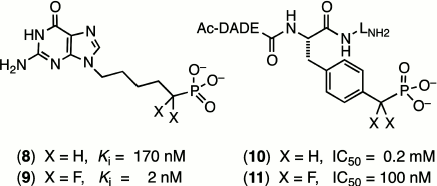
One of the most outstanding examples comes from the extensive studies of Terence Burke on fluoromethylene analogues of tyrosine phosphates. A hexapeptide mimic of AcDADEYpLNH2, with a benzylphosphonate replacing the tyrosine phosphate residue (10), shows a modest inhibition of the tyrosine phosphatase enzyme that is improved 2000-fold on introduction of two α-fluorines in (11) (Scheme 2) [31]. Such effects (reviewed in [16] and [22]) can lie well outside the range that can be attributed simply to an increased acidity of the phosphonate residue (ΔpKa2 ~ –2) and must signal increased binding due to the fluorines. However, as yet there is scant structural data from protein crystallography to indicate whether this results from favourable interaction of the fluorines with the protein or from a solvent entropy effect.
Substitution remote from the catalytic site of the substrate. When the halomethylene substitution is at a phosphate site distant from the reacting centre, a very different scenario exists. The consequences of modified substrate binding or kinetic transformation have to result from direct influences on the strength of “passive” binding and of subtle changes in conformation of the substrate transmitted at a distance to the catalytic centre. A fine early example of this was a study of inhibition of purine nucleotide phosphorylase. While 9-(5′-phosphono-pentyl)guanine (8) is a modest inhibitor of this enzyme, (Ki 170 nM), the introduction of two α-fluorines at the phosphonate locus remote from the reacting centre improved the binding of (9) up to 100-fold (Scheme 2) [32].
As a result of the advent of chiral synthesis of α-fluorophosphonates (v.s.), it has become possible to analyze the separate contribution of the (R)-and (S)-isomers of the same fluorophosphonate analogue to binding or to inhibition. A notable example is a study of glucose 6-phosphate dehydrogenase (GPDH) by David Berkowitz. Unexpectedly, the order of affinity of glucose 6-phosphate and its analogues for the bridging isosteric ligand is O > (S)-CHF > CH2 > CF2 > (R)-CFH with Km values of 0.12 : 0.23 : 0.49 : 1.35 : 2.26 mM, respectively [22]. This result demonstrates that the influence on affinity of a remote fluorophosphonate ligand for a protein can be enhanced by the introduction of fluorine in one stereochemistry yet diminished for the alternative stereochemistry, as was apparent in the earlier work of David O’Hagan on analogues of glycerol 3-phosphate and the corresponding dehydrogenase [33].
It is not therefore surprising that enzymes have been shown to select one diastereoisomer from a mixture of both ligands, as in the case of Samuel Wilson’s recent work on α,β-fluoromethylene-2′-deoxyATP and DNA polymerase beta [34]. However, in this case both the (S)-CHF and the CF2 analogues show clearly reduced affinity relative to the CH2 analogue that is not simply explicable from the associated X-ray structures of the complexes. There is a clear need for an investigation that combines stereospecific synthesis of both stereoisomeric fluorophosphonate analogues, their quantitative binding to the target enzyme, and a high resolution X-ray structural analysis of the resulting complexes. Until then, the role of fluorination in ligand binding to proteins is likely to remain the preserve of the computational and analytical chemists [35].
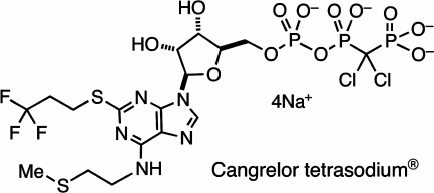
This survey of halophosphonates as remote analogues of biological phosphates cannot be completed without reference to their successful application in medicine. The search for ATP-like antagonists for the P2Y12 receptor led John Dixon in Astra Zeneca, the UK pharmaceutical company, to promote the development of 5′-O-[[[dichloro-(phosphono)methyl](hydroxy)phosphoryloxy](hydroxy)-phosphoryl]-N-[2-(methylsulfanyl)ethyl]-2-(3,3,3-trifluoropropylsulfanyl)adenosine tetrasodium salt, better known as Cangrelor sodium, AR-C69931MX (12) (Scheme 3). This is a metabolically stable and bioavailable analogue of ATP with very high and selective affinity for the P2Y12 receptor and is a valuable intravenous drug for the inhibition of platelet aggregation and use in coronary surgery [36].
STRUCTURAL STUDIES AS A GUIDE TO BIOCATALYSIS
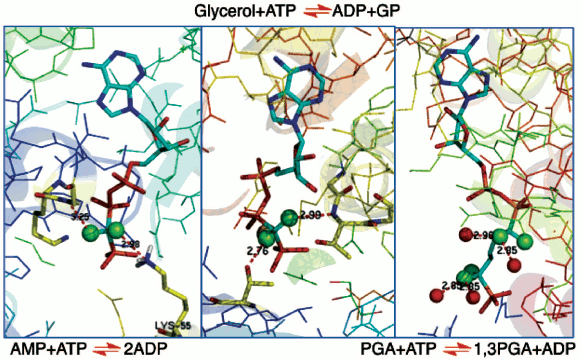
In the 1980s, protein crystallography had made significant advances into the structures of complexes of biological phosphates and cognate enzymes. Achieving structures of enzymes in binary complexes with fluoromethylenephosphonate ligands thus became an accessible means to understanding the biocatalysis of phosphoryl transfer mechanisms. Our work provided substrate analogues that led to structures of β,γ-difluoromethylene ATP with adenylate kinase [37] and with glycerol kinase [38]. These showed domain closure for both of these enzymes (Fig. 6, left and centre; see colour insert). Moreover, in the case of glycerol kinase the orientation of the nucleotide phosphate donor to the nucleophilic oxygen of glycerol proved to be superior for the CF2ATP analogue than for alternative ATP analogues investigated, providing one of the best examples of the useful apicophilicity of the CF2 ligand at phosphorus (v.s.) [38].
We then undertook an extensive study of phosphoglycerate kinase first with a bisubstrate analogue designed to link ADP to a phosphoglycerate-like moiety [39, 40] and then with a range of isosteric and non-isosteric analogues of D-glyceric acid 1,3-bisphosphate (Fig. 6, right) [41, 42]. The results of these investigations give good support for the existence of C-F•••••H-N(O) hydrogen bonds to amino acid residues or to bound waters (Fig. 6), though there is an ongoing controversy about such C-F•••••HN hydrogen bonds [35, 43]. More significantly, it became apparent that ground state studies were an uncertain approach to understanding biocatalysis. For example, in glycerol kinase the γ-phosphorus of the ATPCF2 analogue and the nucleophilic glycerol oxygen are 4.3 Å apart [38]. That distance is well outside the 3.32 Å Van der Waals contact distance, and so it can give little clue to the nature of phosphoryl transfer for this enzyme.Fig. 6. Structures of three enzymes with difluoromethylenephosphonate ligands bound: (left) adenylate kinase with ATPCF2 showing C-F hydrogen bonding to K55 and G17 (PDB: 1DVR) [37]; (centre) glycerol kinase with ATPCF2 and glycerol showing hydrogen bonding to T14 and T267 (PDB: 1BWF) [38]; and (right) phosphoglycerate kinase with a bisubstrate ADP:3PGA analogue having four fluorines showing C-F hydrogen bonding to four waters (PDB: 16PK) [39].
Catalytic antibodies offered a new approach to the biocatalysis of phosphoryl transfer. The focus on enzyme catalysis deriving from transition state affinity, which originated from Haldane [44] and from Pauling [45], had stimulated the development of the field of antibodies that strongly bind to transition state analogues (TSA). Such antibodies should markedly lower the free energy of the transition state for the corresponding chemical reaction, and so should be potential biocatalysts [46]. In practice, their application to phosphoryl transfer reactions presented a huge challenge for synthetic chemistry. If the transition state for phosphoryl transfer has the geometry of an expanded tbp, how can that be mimicked by a stable analogue constructed from the elements of the Periodic Table?
None of the elements giving five coordinate species having five stable oxygen ligands, such as phosphorus, vanadium, tungsten, etc., could survive in water in vivo long enough to enable development of murine antibodies that might be catalysts. After much unsuccessful design and synthesis, we turned to the concept of selecting catalysts from a library of computer-designed, artificial antibodies by using suicide substrates in vitro. After much hard work, that approach eventually delivered an antibody phosphatase that had 0.1% of the activity of native alkaline phosphatase from E. coli [47, 48]. Unfortunately, all attempts to determine the mechanism of this catalysis were unrewarding. So we had to consider how best to use the transition state approach to study the biocatalysis of phosphoryl transfer.
FOCUS ON TRANSITION STATE STUDIES
A paper appeared in Science in 2003 claiming the stable existence of a pentaoxyphosphorane species in a crystal structure of β-phosphoglucomutase (β-PGM) [49]. We read it with care, especially because it had been accorded enthusiastic reception by Jeremy Knowles, one of the doyens of the field, under the title “Seeing is Believing” [50]. We found the phosphorane assignment to be problematic in several respects: P-O bond lengths, thermodynamic considerations, difference map inconsistencies and, above all, conflicts with the results of many years’ investigations of phosphoryl transfer reactions. When we found that the crystals had been prepared in 100 mM ammonium fluoride, we conceived that a tbp complex having trifluoromagnesate with two apical oxygen ligands could be a better interpretation of the published electron density map (PDB: 1O08).
A literature search elicited just one such structure, that of a small G protein, of RhoA·GDP·MgF3– in complex with RhoGAP. This had a tbp moiety linked to Pβ of the tightly-bound GDP (PDB: 1OW3). The evidence that this was a trifluoromagnesate transition state complex was incontrovertible [51]. Nonetheless, because this example was unique, our proposal that the structure of the β-PGM complex was better interpreted as a trifluoromagnesate TSA [52] was strongly rebutted by Karen Allen [53]. Protein crystallography is generally incapable of discriminating between oxygen and fluorine in terms of electron density and bond length at resolutions of structures above 1.0 Å. Therefore, the final solution to this problem called for an alternative spectroscopic analysis. In the case of the RhoA·RhoGAP·GDP complex, that had been provided by proton-induced X-ray emission analysis, PIXE [51]. But the PIXE method demands crystals that are free of contaminating inorganic phosphate, and that is not always readily achievable.
We therefore turned to 19F NMR and had immediate success. Because the chemical shift of the metal fluoride directly identifies the nature of the metal, it is possible to discriminate beryllium, aluminium, magnesium, and gallium fluorides with confidence. With this facility, we have now established that trifluoromagnesate, MgF3–, forms stable complexes with a wide range of phosphoryl transfer enzymes including phosphatases, mutases, and kinases that can readily be identified by the presence of three fluorine signals with chemical shifts in the region –150 to –160 ppm [54-56]. Where needed, these NMR peaks can directly be correlated with high resolution structures of the proteins determined by X-ray crystallography, as in the cases of phosphoserine phosphatase [56], β-PGM [55], and PGK [57].
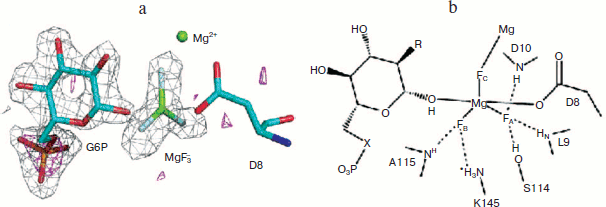
Most particularly, the direct analysis of a high resolution crystal structure of the MgF3– complex of β-PGM (PDB code: 2WF5) and correlation with the 19F NMR structure formed under the conditions of crystallisation finally resolved the controversy in every detail and established that the tbp transition state complex for this enzyme has a trigonal planar trifluoromagnesate core (Fig. 7; see colour insert) [58]. Any examples claimed to be pentaoxyphosphoranes or, indeed, metaphosphates should be regarded with extreme suspicion!
From this beginning, studies in Sheffield on metal fluoride complexes of phosphoryl transfer enzymes have developed in several, significant ways. In particular, in the case of PGK we have been able to generate NMR data for both a tbp trifluoromagnesate complex and an octahedral tetrafluoroaluminate complex and then correlate these with high resolution X-ray structures [57]. Not only does the multiplicity of the fluorine peaks discriminate between the formation of tetrafluoroaluminate complexes (generally below pH 8.5) and the trifluoromagnesate complexes that supersede them above pH 8.5, but the changes in metal fluoride chemical shifts on changing the solvent from H2O to D2O also provide a good measure of the number and strength of hydrogen bonds to each fluorine and confirm the assignment of the highest field signal to that fluorine coordinated to the catalytic magnesium in these enzymes.Fig. 7. a) Structure of the PGM-MgF3–-G6P-TSA complex active site. Difference Fourier map and the anomalous substructure of the PGM-MgF3-G6P-TSA complex. The anomalous difference density is contoured at 3σ (magenta mesh). Phosphorus is identified by a large peak (7.1σ) for glucose 6-phosphate, but no such phosphorus peak is seen in the active site trigonal bipyramidal moiety. That confirms the assignment of the trigonal planar species as MgF3– and not PO3–. The difference electron density (Fo − Fc) from the same data is shown (gray mesh) contoured at 3σ for G6P and the MgF3– moiety before their inclusion in the model. b) Schematic diagram of the active site of the PGM-MgF3–-sugar phosphate-TSA complex. Three sugar moieties have been studied: G6P (R = OH, X = O); 6-deoxy-6-(phosphono-methyl)-D-glucopyranoside (R = OH, X = CH2); and 2-deoxy-G6P (R = H, X = O) (PDB code: 2WF5) [57].
There have been five significant advances from these analyses.
The tetrafluoroaluminate:trifluoroaluminium transition state paradox. Based on a careful comparison of the structures of some 15 transition state complexes of nucleotide kinases, Schlichting and Reinstein proposed [59] that pH influences the fluoride coordination number of the AlFx phosphoryl transfer transition state analogues. Octahedral complexes containing square planar tetrafluoroaluminate, AlF4–, predominated at pH > 7.5 while tbp complexes containing a neutral trigonal aluminium trifluoride moiety, AlF30, were observed at high pH.
One intriguing example of this phenomenon appeared in the work of David Wemmer on phosphoserine phosphatase (PSP) [60]. This showed dual occupancy of the active site, assigned as 60% octahedral AlF4– and 40% tbp AlF30. In our hands, the 19F NMR of the complex in the absence of aluminium gave the three peaks typical of an MgF3– complex. However, the addition of two equivalents of aluminium chloride resulted in the immediate transformation of the spectrum into the four peaks typical of an AlF4– complex. We therefore recorded the 19F NMR spectrum as we titrated the aluminium sample incrementally from pH 6 to higher pH. As the pH rose above 8, the four signals for AlF4– grew weaker and disappeared, while three signals identical with those for the MgF3– complex superseded them. There were no conditions under which we could observe signals for an AlF30 complex. Two conclusions were unavoidable. First, raising the pH result in precipitation of aluminium(III) so that magnesium, by default, forms a trifluoromagnesate tbp complex. Second, the predominance of the AlF4– complex rather than an AlF30 complex at pH 6 to 8 shows that the enzyme prioritizes anionic charge over tbp geometry in the transition state analogue [55]. Far from being an isolated result, we have now identified the same pH transition from octahedral tetrafluoroaluminate at low pH to tbp trifluoromagnesate at high pH for four further enzyme transition state complexes, β-PGM, PGK, protein kinase A (PKA), and UMP/CMP kinase, each of which has been described as having an AlF30 complex at high pH. It therefore seems probable that a large proportion of the many entries in the Protein Data Bank assigning a tbp complex to the ligand aluminium trifluoride (PDB code: AF3, 40 entries) are really trifluoromagnesate complexes (PDB code: MGF, 8 entries) or cases of mixed occupancy.
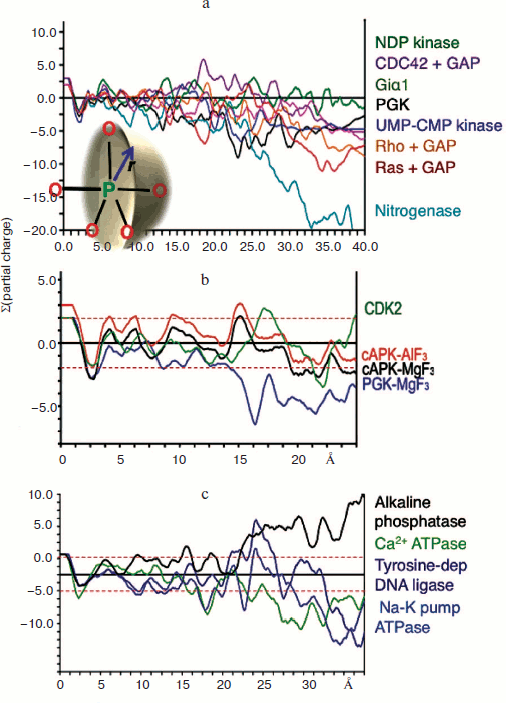
Charge balance hypothesis. Given the opportunity of recognising tbp transition state complexes to be built around a trigonal planar trifluoromagnesate anion rather than a neutral aluminium trifluoride moiety, it now became possible to make direct comparisons between TSAs for tetrafluoroaluminate and trifluoromagnesate and other trigonal planar cores on the basis of net charge. Our initial analysis of a range of kinases was based on the summation of Pauling charges within a sphere of radius r centred on the transferring phosphorus atom (or its Mg/Al surrogate) as shown (Fig. 8 inset; see colour insert). It was gratifying to find that charges sum close to zero (±2 charges) within a radius approaching 15 Å for a sample of seven kinases while nitrogenase, as a control, did not show this behaviour (Fig. 8a) [57, 61]. We have extended this analysis to a range of enzymes under current analysis by 19F NMR and having high resolution protein structures (Fig. 8b) and have not yet found an exception to charge balance for a wild type protein. Indeed, we have extended the concept to a range of proteins having very different biocatalytic activities, including alkaline phosphatase, calcium ATPase, sodium potassium pump ATPase, and the vanadate complex of a tyrosine-dependent DNA ligase, and found the results very satisfactory (Fig. 8c). Charge balance appears to be a useful and likely a very significant tool to understand how the transition state for biocatalysis of phosphoryl transfer extends into the second shell of residues around the active complex and perhaps further.
General acid-base catalysis and phosphoryl transfer. The very large number of high resolution structures in the Protein Data Bank for metal fluoride and vanadate transition state complexes of phosphoryl transfer enzymes makes possible a detailed analysis of their general characteristics. Two components of TSAs are clearly defined. The first is the anionic character of the donor and acceptor ligands for the transferring phosphoryl group. That conclusion is reached both by inspection of tbp TSAs based on trifluoromagnesate, “aluminium trifluoride”, or metavanadate complexes but also by deduction from octahedral TSAs based on tetrafluoroaluminate [61]. The two apical oxygen ligands in the penta-coordinate phosphorus array are, almost without exception, partially or fully negatively charged. That is directly manifest in the case of anionic phosphoryloxy and carboxylate anionic ligands as in the case of PGK [57]. Neutral hydroxyl groups, phenolic for tyrosine, hydroxylic for serine, threonine, and sugars, are invariably hydrogen bonded to a general base catalyst, most frequently an essential aspartate residue. Thus, for β-PGM, the anionic carboxyl of Asp8 is axially complemented by the nucleophilic glucose-1 hydroxyl group that, in turn, is strongly hydrogen bonded (2.7 Å) to anionic Asp10. This high resolution structure has been analyzed using ONIOM (B3LYP:PM3MM) calculations to address the nature of the PGM active site [62]. These confirm that the TS is concerted ANDN [63] and has an expanded five-coordinate phosphorus deploying concomitant proton transfer from the 1-hydroxyl group of glucose to the carboxylate of Asp10.Fig. 8. Charge balance measured by summing Pauling charges within a sphere of radius r centred on phosphorus (inset). a) Charge balance for seven kinases with nitrogenase for comparison. b) Charge balance for PGK, β-PGM, and PKA [65]. c) Charge balance for alkaline phosphatase, Ca2+ ATPase, Na+/K+ pump ATPase, and Tyr-dependent DNA ligase.
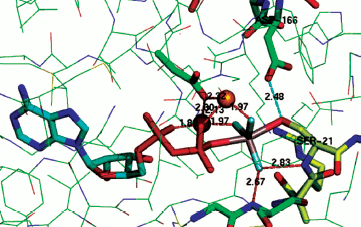
The same is the case for phosphoserine phosphatase. Here the nucleophilic carboxylate Asp11 is axially opposed by the hydroxyl of the serine substrate that is strongly hydrogen bonded to Asp13 (2.68 Å, PDB: 1L7N) [55, 64]. In the case of the archetypical serine protein kinase A (PKA), the transition state complex assigned as AlF30 shows the bridging oxygen of the ATP phosphate donor is axially opposed by the serine hydroxyl from the substrate peptide, Ser21, with a strong hydrogen bond (2.48 Å) to Asp166 (PDB: 1L3R) (Fig. 9; see colour insert) [65]. A sulfur-vanadium variation is shown in a recent study of the protein tyrosine phosphatase PTYP1B by Sean Johnson (PDB: 3I7Z) [66]. This identifies a tbp TSA having a trigonal planar metavanadate core with the axial thiolate of Cys215 axially opposed by the hydroxyl of tyrosine in the DADEYL hexapeptide that is strongly hydrogen bonded (2.61 Å) to the catalytic Asp181.
A contrary view comes from a recent study of the thermodynamics of kinase activity. Richard Wolfenden has singled out N-acetylglucosamine kinase as an example that does not employ general acid-base catalysis for phosphoryl transfer [67]. However, inspection of human N-acetyl galactosamine kinase complexed with Mg-ADP and N-acetyl galactosamine 1-phosphate shows that, even in the ground state complex, the phosphate bridging oxygen forms a long hydrogen bond to Asp190 (3.2 Å, PDB: 2A2C) [68]. It appears that for high-resolution X-ray structures, there is no exception to the identification of general acid-base catalysis in phosphoryl transfer.Fig. 9. Structure of TSA for protein kinase A with Ser21 of substrate peptide (yellow) complexed in a tbp metal trifluoride moiety with ADP in the opposing axial position. Coordination of the TSA to two catalytic magnesiums (orange) shown in red and a strong hydrogen bond (2.48 Å) from catalytic Asp166 to Ser21 shown in cyan [65].
Nature of phosphoryl transfer. In the early days of mechanistic analysis of phosphoryl transfer, much attention was devoted to the possibility of “adjacent” attack with a 90° angle between the incoming and leaving groups of a tbp complex. That gave rise to the whole topic of pseudorotation [69]. Today “in-line” attack of the nucleophile is virtually universal. One isolated case of a mutase may be an exception: Oznat Herzberg has argued [70] that phosphoenol pyruvate mutase biocatalysis proceeds via a mechanism in which the pyruvoyl carbon-3 adds to the same face of the migrating phosphoryl group as that from which oxygen-2 departs. This analysis accords with the observed retention stereochemistry at phosphorus. In all other cases, retention of stereochemistry is interpreted as a double inversion with two successive “in-line” substitutions at phosphorus [71].
With this stereochemical issue put to bed, recent attention has focused on the question of the associative or dissociative nature of phosphoryl transfer. Initial discussions put emphasis on bond length considerations. By this criterion, a fully dissociative process (DN + AN) [63] was perceived, in extremo, to involve a stable, three-coordinate metaphosphate anion, PO3–, of which Frank Westheimer was a strong proponent [72]. At the other extreme, a fully associative process (AN + DN) should involve a stable penta-coordinate phosphorane with an axial O-P-O distance of 3.32 Å [73]. In between these extremes, there is a continuum of mechanistic possibilities with a concerted mechanism (ANDN) being described as a single-step reaction proceeding through a single transition state [74]. If the O-P•••••O distance is taken as that of a P–O bond plus the combined Van der Waals radii of phosphorus and oxygen, then a dissociative process can be considered to involve an enzyme complex in which the reacting oxygens are over 5.0 Å apart.
However, bond orders have come strongly into the discussion, largely from their use in the interpretation of primary and secondary kinetic isotope effects (for 32P and 18O). As in the case of established instances in carbon chemistry [75], their application generally leads to a more dissociative description of transition states and typically for aryl phosphate ester hydrolysis ([76] and references therein). For the purposes of describing biocatalysis, this dichotomy needs to be resolved.
What are the relative merits of the two different methods of analysis? Bond lengths are directly measurable, they are amenable to computational analysis, and they are inversely related to bond strength. Moreover, kinetic isotope effects can be computed from structure analysis. By contrast, bond orders cannot be measured directly; they are an exponential transform from bond lengths using an empirical equation (Eq. (1)) from Linus Pauling [77] who assigned a value of 0.3 Å for the constant b. However, other values up to 0.7 Å have been used for phosphate reactions and a value of 0.6 Å has been considered more appropriate for transition states involving carbon–carbon and carbon–oxygen bonds [75]. In addition, bond orders are not used directly in computations of transition states.
The same analysis can be applied to the phosphoryl transfer enzyme transition state analogues examined by 19F NMR and cognate X-ray structures. For β-PGM [58] the equivalent O–P–O measurements in the MgF3– TSA are 4.27 Å and 175.7°; for PSP the data are 4.21 Å and 175.95° [55]; for PGK they are 4.27 Å and 170.91° [57], and for the AlF30 TSA for PKA they are 4.26 Å and 162.18° [65]. These and many other reactions involving biocatalysis of transfer of the phosphoryl group, PO3–, clearly fall into the category of concerted-associative reactions.
It might be argued that these geometries are imposed by the nature of the metal fluoride TSAs and do not accurately reflect the true phosphorus-based transition state. That seems unlikely to us, not least because the metal-fluoride bonding is at least 80% ionic in character. Moreover, kindred results can be derived from metavanadate complexes, as for the recent structure of a nucleoside diphosphate kinase with ADP linked through vanadate to His134. This shows O–P–N distance of 4.48 Å and an angle of 172.11° (PDB: 4DZ6). In addition, computation of transition states for phosphoryl transfer based on such TSAs as starting points delivers very similar bond lengths and angles to those measured by X-ray diffraction [62].
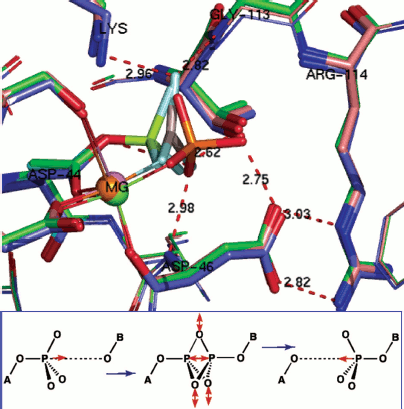
Phosphoryl transfer means phosphorus translocation. Structure analysis can go still one stage further. For a growing number of enzymes, it is possible to overlay X-ray structures for substrate complex, TSA complex, and product complex. We have done that for hPGK, β-PGM, and PSP [78] while it can also been done for PKA [65], for an AphA acid phosphatase from E. coli [79], and for a human diphosphoinositol pentakisphosphate kinase (table) [80]. In the case of AphA acid phosphatase, structures are available for a BeF3– mimic of an aspartyl phosphate substrate complex (PDB: 2HEG), for an AlF30 TSA complex (PDB: 2HF7), and for an inorganic phosphate product complex (PDB: 1RMY). When these are overlaid with all the α-carbons aligned, it is immediately clear that the active sites show good superposition of the catalytic magnesiums (Fig. 10, upper; see colour insert). Moreover, all the catalytically active residues, notably Asp44, Asp46, Thr112, Arg114, and Lys152, also align very well.
Data from triple overlays for five phosphoryl transfer enzymes: two GS and one TSA complexes in each case (data taken from respective PDB entries)Fig. 10. (upper) Triple overlay of E. coli acid phosphatase with aspartyl phosphate substrate complex (PDB: 2HEG, cyan), AlF30 TSA complex (PDB: 2HF7, green), and inorganic phosphate product complex (PDB: 1REMY, purple) [78]. Catalytic magnesium and all catalytic amino acid residues overlay accurately for the three structures. The reacting moieties show the near constancy in position of the equatorial oxygens while they well define the transition of phosphorus through their triangle. (Hydrogen bonds shown for TSA complex). (lower) Concerted-associative pathway for phosphoryl transfer. A-O is the donor axial ligand and B-O is the acceptor. Negative charges and general acid-base catalysis is ignored for simplicity. In the pre-transition state (centre) the equatorial oxygens move outwards at the TS and the phosphorus migrates through the trigonal plane of the phosphoryl group.
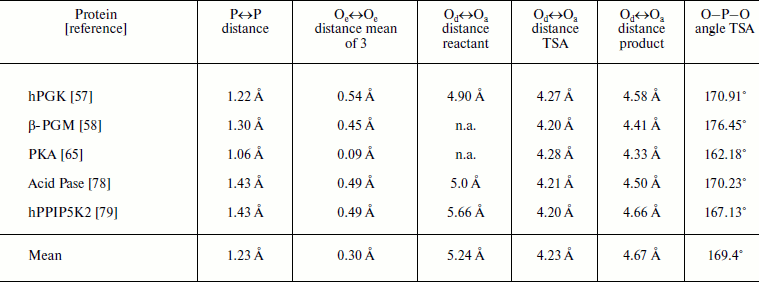
Note: P↔P distance measured from reactant to product GS overlays; Oe↔Oe, equatorial oxygen translocation distances between the two GS complexes; Od↔Oa, apical-apical distances measured from reactant GS, TSA, and product GS complexes; O–P–O, angle from TSA complex; Pase = phosphatase; n.a., not available.
Taken together, this analysis of the transferring phosphoryl moiety in the five structures provides compelling evidence for an associative phosphoryl transfer mechanism. The remarkable result is that for the three overlaid structures in each of the five examples, the three non-bonding oxygens, mimicked by equatorial fluorines in the tbp metal trifluoride complexes, and the three pairs of axial, reactant/product oxygens not only occupy the same loci and with the same coordination partners, they show very little movement in progress from reactant to transition state to product (Fig. 10, upper). The key data are presented in the table. These show that the average distance of movement from reactant to product for the fifteen equatorial oxygens is only 0.30 Å (column 3), the average separation distance of the axial oxygens in the five transition states is 4.23 Å (column 5), and the average distance of translocation of phosphorus from reactant to product (column 2) is 1.20 Å. What these structures further illustrate is that there is a small movement of reactants towards each other in progressing from reactants to their transition states of around 1.0 Å, and they recoil by around 0.5 Å in progressing to the product complexes. In all five cases, the “in-line” character of the TSA complex is almost exact, with an average value of 169°. These five reactions are all concerted-associative processes (Fig. 10, lower).
It has to be concluded that in these enzyme-catalyzed phosphoryl transfer processes, it is phosphorus that migrates as the reaction proceeds, not the phosphate moiety! The enzyme coordinates the equatorial oxygens with magnesium (1 or 2 catalytic magnesiums are commonly observed) and/or neutral hydrogen bond donors that are “tuned” to accommodate the trigonal bipyramidal transition state of the phosphoryl group better than the ground states of the phosphate moieties. The barrier to such a facile process in uncatalyzed solution owes much to the anionic shield that surrounds anionic phosphate esters and anhydrides and makes attack by a nucleophile very costly [61]. For these phosphoryl transfer enzymes, the enzyme first constructs an active site that counterbalances the charge(s) in the reactants and products. Then it applies general acid-base catalysis to minimize repulsion of the approach of a hydroxyl nucleophile and facilitate departure of a poor leaving group. Evolution found it amazingly uncomplicated to catalyze phosphoryl group transfer!
NEAR ATTACK CONFORMERS, NACs
This analysis of reaction mechanisms so far has focused strongly on the role of the transition state for biocatalysis. While the stabilization of transition states (TS) is, indeed, crucial for the very effective catalysis achieved by enzymes, the studies we have discussed hitherto have a chemical transformation step, where the reacting species have partial chemical bonding character. Yet it is clear that enzymes have to avoid substantial barriers associated with nonchemical transformation steps and so may have to stabilize other regions of the multi-dimensional energy surface corresponding to the reaction coordinate. The concept of near attack conformers (NACs) was introduced by Tom Bruice as a useful tool to help the analysis of these different roles, simply achieved by partitioning chemical transformation and nonchemical transformation steps [81]. This thesis has been primarily developed for relatively simple enzyme processes, notably chorismate mutase [82], but has had little direct experimental verification.
We have studied tetrahedral mimics of stable, intermediate phosphate species by the use of trifluoroberyllate (BeF3–) complexes by a combination of 19F NMR and protein crystallography, and this has recently provided much-needed experimental evidence for NACs [8]. These direct observations of ground state analogue complexes of β-PGM involving BeF3– establish that when the geometry and charge distribution closely match those of the substrate, then the distribution of conformers in solution and in the crystal predominantly places the reacting centres in Van der Waals proximity.
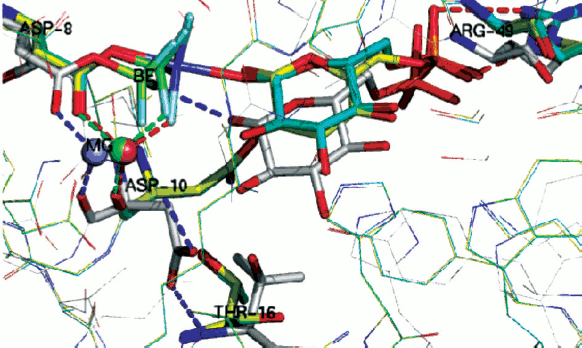
Importantly, two variants have been found for β-PGM, both of which satisfy the criteria for near attack conformers (NACs). In NAC-I, the Asp10 general base for the reaction is remote from the nucleophile, which thus remains protonated (Fig. 11, silver; see colour insert). Instead, it forms a non-productive hydrogen bond to the phosphate surrogate. In NAC-II (Fig. 11, yellow), the Asp10 general base forms a hydrogen bond to the glucose 1-OH nucleophile that is now correctly orientated for the chemical transfer step. In the transition state (TSA; Fig. 11, cyan) the nucleophile is activated by Asp10 and comes even closer to the phosphate surrogate. By contrast, in the absence of glucose 1-phosphate substrate, the solvent surrounding the phosphate surrogate is arranged to disfavour nucleophilic attack by water on the aspartyl phosphate and so enhances its stability to deleterious hydrolysis. Taken together, these trifluoroberyllate complexes of β-PGM provide a picture of how the enzyme is able to organize itself for the chemical step in catalysis through the population of intermediates that respond to increasing proximity of the nucleophile.
Phosphate mono- and di-esters are among the most stable species with respect to spontaneous hydrolysis under physiological conditions, with half lives around 1012 and 3·107 years, respectively [83]. The central paradox of the universality of phosphate esters for life [61] is the fundamental use of such stability for structural purposes, most notably for the backbone of DNA, contrasted with the necessity of manipulating phosphate esters on the millisecond time scale needed for signalling. To meet that challenge, evolution has delivered enzymes capable of manipulating phosphate ester cleavage with turnover numbers up to 103 sec–1. That places such enzymes among the most proficient of all biocatalysts, with rate accelerations of the order of 1021 [84].Fig. 11. Two near attack conformations for β-PGM. NAC-I (silver), NAC-II (yellow), and TSA (cyan) with substrate glucose 1-phosphate bound. Progressive approach to the transition state shown by movement of (i) beryllium (green) to magnesium (blue) trifluoride; of (ii) catalytic magnesium (orange) and especially of (iii) catalytic Asp10 from open conformation (silver) to closed conformation (yellow, cyan) enabling H-bonding to glucose 1-OH group. (Ligands/H-bonds in blue for NAC-I, in green for NAC-II, and in red for TSA).
Understanding the nature of such catalysis is a prime challenge that is now into its second half-century of exploration. It has been the purpose of this survey to demonstrate the great advances in our knowledge that have come about through the ability to deploy stable mimics of ground states and transition states for wild type enzymes with natural substrates. It has identified the value of covalent, Lewis acid, general acid-base, alignment, and proximity catalysis effects in a variety of combinations as well as revealing the wide adoption of charge complementation between substrate(s) and residues in the region around the enzyme active site.
While there are still many details to be explored, and perhaps further results to be reinterpreted, a major challenge for the future is the need to make similar progress on transition state analysis for biocatalysis of phosphate diesters.
We are indebted to many co-workers and collaborators and especially to Drs. Nicola Baxter and Matthew Cliff.
We thank BBSRC, EPSRC, and the University of Sheffield for financial support.
REFERENCES
1.Blackburn, G. M., Cohen, J. S., and Todd, A. R.
(1964) Tetrahedron Lett., 5, 2873-2879.
2.Blackburn, G. M., Brown, M. J., and Harris, M. R.
(1966) J. Chem. Soc. Chem. Commun., 611-612.
3.Blackburn, G. M., Brown, M. J., Harris, M. R., and
Shire, D. (1969) J. Chem. Soc. Perkin, 1, 676-683.
4.Smith, J. D., Traut, R. R., Blackburn, G. M., and
Monro, R. E. (1965) J. Mol. Biol., 13,
617-628.
5.Hansen, J. L., Schmeing, T. M., Moore, P. B.,
and Steitz, T. A. (2002) Proc. Natl. Acad. Sci. USA,
99, 11670-11675.
6.Blackburn, G. M., and Brown, M. J. (1969) J. Am.
Chem. Soc., 91, 525-526.
7.Storm, D. R., and Koshland, D. E. (1970) Proc.
Natl. Acad. Sci. USA, 66, 445-452.
8.Griffin, J. L., Bowler, M. W., Baxter, N. J.,
Leigh, K. N., Dannatt, H. J. R., Hounslow, A. M., Blackburn, G. M.,
Webster, C. E., Cliff, M. J., and Waltho, J. P. (2012) Proc. Natl.
Acad. Sci. USA, DOI/10.1073/pnas.1116855109.
9.Blackburn, G. M. (1981) Chem. Ind. (London),
5, 134-138.
10.Orr, G. A., and Knowles, J. R. (1974) Biochem.
J., 141, 721-723.
11.McAleese, S. M., Jutagir, V., Blackburn, G. M.,
and Fothergill-Gilmore, L. A. (1987) Biochem. J., 243,
301-304.
12.Richard, V., Dodson, G. G., and Maugen, Y. (1993)
J. Mol. Biol., 233, 270-274.
13.Larsen, T. M., Benning, M. M., Rayment,
I., and Reed, G. H. (1998) Biochemistry, 37,
6247-6255.
14.Blackburn, G. M., Kent, D. E., and Kolkmann, F.
(1981) J. Chem. Soc. Chem. Commun., 1188-1190.
15.Burton, D. J., and Flynn, R. M. (1979)
Synthesis, 615.
16.Romanenko, V. D., and Kukhar, V. P. (2006)
Chem. Rev., 106, 3868-3935.
17.Blackburn, G. M., and Ingleson, D. (1978) J.
Chem. Soc. Chem. Commun., 870-871.
18.McKenna, C. E., and Schmidhauser, J. (1979) J.
Chem. Soc. Chem. Commun., 739.
19.D’yakov, V. M., Voronkov, M. G., and Orlov,
N. F. (1972) Izvestiya Akad. Nauk SSSR. Ser. Khim., 11,
2484-2488.
20.Blackburn, G. M., and Rashid, A. (1988) J.
Chem. Soc. Chem. Commun., 40-41.
21.Blackburn, G. M., and Rashid, A. (1988) J.
Chem. Soc. Chem. Commun., 317-319.
22.Berkowitz, D., Pfannenstield, T. J., and Doukov,
T. (2000) J. Org. Chem., 65, 4498-4508; Berkowitz, D.,
and Bose M. (2001) J. Fluorine Chem., 112, 13-33.
23.Wu, Y., Zakharova, V. M., Kashemirov, B. A.,
Goodman, M. F., Batra, V. K., Wilson, S. H., and McKenna, C. E. (2012)
J. Am. Chem. Soc., DOI: 10.1021/ja300218x.
24.Bhattasali, D., Forget, S. M., and Jakeman, D. L.
(2012) in preparation.
25.Blackburn, G. M., Kent, D. E., and Kolkmann, F.
(1984) J. Chem. Soc. Perkin Trans., 1, 1119-1125.
26.Blackburn, G. M., Eckstein, F., Kent, D. E., and
Perrée, T. D. (1985) Nucleosides Nucleotides, 4,
165-167.
27.Bisbal, C., Silhol, M., Lemaitre, M., Bayard, B.,
Salehzada, T., Lebleu, B., Perrée, T. D., and Blackburn, G. M.
(1987) Biochemistry, 26, 5172-5178.
28.Dixon, R. E., and Lowe, G. (1989) J. Biol.
Chem., 264, 2069-2074.
29.McLennan, A. G., Taylor, G. E., Prescott, M., and
Blackburn, G. M. (1989) Biochemistry, 28, 3868-3875.
30.Sucato, C. A., Upton, T. G., Kashemirov, B. A.,
Osuna, Oertell, J. K., Beard, W. A., Wilson, S. H., Florian, J.,
Warshel, A., McKenna, C. E., and Goodman, M. F. (2008)
Biochemistry, 47, 870-879.
31.Burke, T. R., Jr., Kole, H. K., and Roller, P. P.
(1994) Biochem. Biophys. Res. Commun., 204, 129-136.
32.Halazy, S., Ehrhard, E., and Danzin, C. J. (1991)
J. Am. Chem. Soc., 113, 315-319.
33.Nieschalk, J., and O’Hagan, D. (1995) J.
Chem. Soc. Chem. Commun., 719-720.
34.Chamberlain, B. T., Batra, V.
K., Beard, W. A., Kadina, A. P., Shock, D.
D., Kashemirov, B. A., McKenna, C. E., Goodman, M. F.,
and Wilson, S. H. (2012) Chembiochem, 13,
528-530.
35.Dalvit, C., and Vulpetti, A. (2011)
ChemMedChem, 6, 104-114.
36.Srinivasan, S., Mir, F., Huang, J. S., Khasawneh,
F. T., Lam, S. C.-T., and Le Breton, G. C. (2009) J. Biol.
Chem., 284, 16108-16117.
37.Schlauderer, G. J., Proba, K.,
and Schulz, G. E. (1996) J. Mol. Biol., 256,
223-227.
38.Bystrom, C. E., Pettigrew, D. W., Branchaud, B.
P., O’Brien, P., and Remington, S. J. (1999) Biochemistry,
38, 3508-3518.
39.Bernstein, B. E., Williams, D. M., Bressi, J. C.,
Kuhn, P., Gelb, M. H., Blackburn, G. M., and Hol, W. G. J. (1998) J.
Mol. Biol., 279, 1137-1148.
40.Williams, D. M., Jakeman, D. L., Vyle, J. S.,
Williamson, M. P., and Blackburn, G. M. (1998) Bioorg. Med. Chem.
Lett., 8, 2603-2608.
41.Blackburn, G. M., Jakeman, D. L., Ivory, A. J.,
and Willliamson, M. P. (1994) Bioorg. Med. Chem. Lett.,
4, 2573-2578.
42.Caplan, N. A., Pogson, C. I., Hayes, D. J., and
Blackburn, G. M. (1998) Bioorg. Med. Chem., 8,
515-520.
43.Cormanich, R. A., Freitas, M. P., Tormena, C. F.,
and Rittnera, R. (2012) RSC Advances, DOI:
10.1039/c2ra00039c.
44.Haldane, J. B. S. (1930) Enzymes, Green,
London.
45.Pauling, L. (1948) Nature (London),
161, 707-708.
46.Blackburn, G. M., Datta, A., Denham, H., and
Wentworth, P. (1998) Adv. Phys. Org. Chem., 31,
249-392.
47.Betley, J. R., Cesaro-Tadic, S., Mekhalfia, A.,
Rickard, J. H., Denham, H., Partridge, L. J., Pluckthun, A., and
Blackburn, G. M. (2002) Angew. Chem. Internat. Ed. Engl.,
41, 775-777.
48.Cesaro-Tadic, S., Lagos, D., Honegger, A.,
Rickard, J. A., Mekhalfia, A., Partridge, L. J., Blackburn, G. M., and
Pluckthun, A. (2003) Nature Biotechnol., 21, 679-685.
49.Lahiri, S. D., Zhang, G., Dunaway-Mariano, D.,
and Allen, K. N. (2003) Science, 299,
2067-2069.
50.Knowles, J. (2003) Science, 299,
2002-2003.
51.Graham, D. L., Lowe, P. N., Grime, G.
W., Marsh, M., Rittinger, K., Smerdon, S.
J., Gamblin, S. J., and Eccleston, J. F. (2002) Chem.
Biol., 9, 375-381.
52.Blackburn, G. M., Williams, N. H., Gamblin, S.
J., and Smerdon, S. J. (2003) Science, 301, 1184.
53.Allen, K. N., and Dunaway-Mariano, D. (2003)
Science, 301, 1184; and subsequent publications.
54.Baxter, N. J., Olguin, L. F., Golicnik, M., Feng,
G., Hounslow, A. M., Bermel, W., Blackburn, G. M., Hollfelder, F.,
Waltho, J. P., and Williams, N. H. (2006) Proc. Natl. Acad. Sci.
USA, 103, 14732-14737.
55.Baxter, N. J., Blackburn, G. M., Marston, J. P.,
Hounslow, A. M., Cliff, M. J., Bermel, W., Williams, N. H., Hollfelder,
F., Wemmer, D. E., and Waltho, J. P. (2008) J. Am. Chem. Soc.,
130, 3952-3958.
56.Baxter, N. J., Hounslow, A. M., Bowler, M. W.,
Williams, N. H., Blackburn, G. M., and Waltho, J. P. (2009) J. Am.
Chem. Soc., 131, 16334-16335.
57.Cliff, M. J., Bowler, M. W., Varga, A., Marston,
J. P., Szabo, J., Hounslow, A. M., Baxter, N. J., Blackburn, G. M.,
Vas, M., and Waltho, J. P. (2010) J. Am. Chem. Soc., 132,
6507-6516.
58.Baxter, N. J., Bowler, M. W., Alizadeh, T.,
Cliff, M. J., Hounslow, A. M., Wu, B., Berkowitz, D. B., Williams, N.
H., Blackburn, G. M., and Waltho, J. P. (2010) Proc. Natl. Acad.
Sci. USA, 107, 4555-4560.
59.Schlichting, I., and Reinstein, J. (1999) Nat.
Struct. Biol., 6, 721-723.
60.Wang, W., Cho, H. S., Kim,
R., Jancarik, J., Yokota, H., Nguyen, H.
H., Grigoriev, I. V., Wemmer, D. E., and Kim, S. H. (2002)
J. Mol. Biol., 319, 421-431.
61.Bowler, M. W., Cliff, M. J., Waltho, J. P., and
Blackburn, G. M. (2010) New J. Chem., 34, 784-794.
62.Webster, C. E. (2004) J. Am. Chem. Soc.,
126, 6840-6841.
63.Guthrie, R. D., and Jencks, W. P. (1989) Acc.
Chem. Res., 22, 343-349.
64.Bowler, M. E., unpublished results.
65.Madhusudan, A. P., Xuong, N. H., and Taylor, S.
S. (2002) Nat. Struc. Biol., 9, 273-277.
66.Brandao, T. A. S., Hengge, A. C., and Johnson, S.
J. (2010) J. Biol. Chem., 285, 15874-15883.
67.Stockbridge, R. B., and Wolfenden, R. (2009)
J. Biol. Chem., 284, 22747-22757.
68.Thoden, J. B., and Holden, H. M. (2005) J.
Biol. Chem., 280, 32784-32791.
69.Westheimer, F. H. (1970) Acc. Chem. Res.,
1, 70-78.
70.Liu, S., Lu, Z., Jia, J., Dunaway-Mariano, D.,
and Herzberg, O. (2002) Biochemistry, 41,
10270-10276.
71.Hengge, A. C. (2005) Adv. Phys. Org.
Chem., 40, 49-108.
72.Westheimer, F. H. (1981) Chem. Rev.,
81, 313-326.
73.Davies, J. E., Kirby, A. J., and Roussev,
C. D. (2001) Acta Crystallogr., E57, o994.
74.Lassila, J. K., Zalatan, J. G., and Herschlag, D.
(2011) Annu. Rev. Biochem., 80, 669-702.
75.Houk, K. N., Gustafson, S. M., and Black, K. A.
(1992) J. Am. Chem. Soc., 114, 8565-8572.
76.Zalatan, J. G., Catrina, I., Mitchell, R.,
Grzyska, P. K., O’Brien, P. J., Herschlag, D., and Hengge, A. C.
(2007) J. Am. Chem. Soc., 129, 9879-9898.
77.Pauling, L. (1947) J. Amer. Chem. Soc.,
69, 542-553.
78.Bowler, M. J. (2012) unpublished results.
79.Calderone, V., Forleo, C., Benvenuti, M.,
Rossolini, G. M., Thaller, M. C., Mangani, S., to be published
(PDB: 1RMY).
80.Wang, H., Falck, J. R., Hall, T. M., and Shears,
S. B. (2011) Nat. Chem. Biol., 8, 111-116.
81.Bruice, T. C. (1976) Annu. Rev. Biochem.,
45, 331-373.
82.Hur, S., and Bruice, T. C. (2003) Proc. Natl.
Acad. Sci. USA, 100, 12015-12020.
83.Lad, C., Williams, N. H., and Wolfenden, R.
(2003) Proc. Natl. Acad. Sci. USA, 100, 5607-5610.
84.Schroeder, G. K., Lad, C., Wyman, P., Williams,
N. H., and Wolfenden, R. (2006) Proc. Natl. Acad. Sci. USA,
103, 4052-4055.