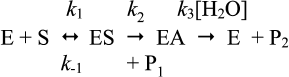Time-Dependent Kinetic Complexities in Cholinesterase-Catalyzed Reactions*
P. Masson1,2,3
1Institut de Recherches Biomédicales des Armées-CRSSA, Dept. Toxicologie, BP 87, 38702 La Tronche cedex, France; E-mail: pmasson@unmc.edu2Institut de Biologie Structurale, Laboratoire de Biophysique Moléculaire, 38027 Grenoble cedex, France
3University of Nebraska Medical Center, Eppley Institute, Omaha, NE 68198-5950, USA
*In memory of Boris N. Goldstein (1943-2011). Boris N. Goldstein was not only a distinguished scientist who applied the graph theory to formal enzyme kinetics, he was also a fabulous palindrome creator (B. N. Goldstein, Palindromes, Foton-vek, Pushchino, 2009, 112 p.). In homage to Boris, I would like to show French avatar of the famous Latin palindrome, known as the Sator square, initially found in the ruins of Pompeii:
The picture is an example of this magic square as inserted in a house door of the old Grenoble, France.
Received April 13, 2012
Cholinesterases (ChEs) display a hysteretic behavior with certain substrates and inhibitors. Kinetic cooperativity in hysteresis of ChE-catalyzed reactions is characterized by a lag or burst phase in the approach to steady state. With some substrates damped oscillations are shown to superimpose on hysteretic lags. These time dependent peculiarities are observed for both butyrylcholinesterase and acetylcholinesterase from different sources. Hysteresis in ChE-catalyzed reactions can be interpreted in terms of slow transitions between two enzyme conformers E and E′. Substrate can bind to E and/or E′, both Michaelian complexes ES and Ε′S can be catalytically competent, or only one of them can make products. The formal reaction pathway depends on both the chemical structure of the substrate and the type of enzyme. In particular, damped oscillations develop when substrate exists in different, slowly interconvertible, conformational, and/or micellar forms, of which only the minor form is capable of binding and reacting with the enzyme. Biphasic pseudo-first-order progressive inhibition of ChEs by certain carbamates and organophosphates also fits with a slow equilibrium between two reactive enzyme forms. Hysteresis can be modulated by medium parameters (pH, chaotropic and kosmotropic salts, organic solvents, temperature, osmotic pressure, and hydrostatic pressure). These studies showed that water structure plays a role in hysteretic behavior of ChEs. Attempts to provide a molecular mechanism for ChE hysteresis from mutagenesis studies or crystallographic studies failed so far. In fact, several lines of evidence suggest that hysteresis is controlled by the conformation of His438, a key residue in the catalytic triad of cholinesterases. Induction time may depend on the probability of His438 to adopt the operative conformation in the catalytic triad. The functional significance of ChE hysteresis is puzzling. However, the accepted view that proteins are in equilibrium between preexisting functional and non-functional conformers, and that binding of a ligand to the functional form shifts equilibrium towards the functional conformation, suggests that slow equilibrium between two conformational states of these enzymes may have a regulatory function in damping out the response to certain ligands and irreversible inhibitors. This is particularly true for immobilized (membrane bound) enzymes where the local substrate and/or inhibitor concentrations depend on influx in crowded organellar systems, e.g. cholinergic synaptic clefts. Therefore, physiological or toxicological relevance of the hysteretic behavior and damped oscillations in ChE-catalyzed reactions and inhibition cannot be ruled out.
KEY WORDS: cholinesterase, pre-steady state, hysteresis, time-dependent, preexisting slow equilibrium, enzyme conformer, damped oscillations, inhibitionDOI: 10.1134/S0006297912100070
Abbreviations: AAA, aryl-acylamidase; AChE, acetylcholinesterase; ASCh, acetylthiocholine; ATMA, 3-(acetamido) N,N,N-trimethylanilinium; BSA, bovine serum albumin; BuCh, butyrylcholine; BuChE, butyrylcholinesterase; BuSCh, butyrylthiocholine; BzCh, benzoylcholine; BzSCh, benzoylthiocholine; CBDP, cresyl saligenin phosphate; ChE, cholinesterase; MNPCC, N-methyl-N-(2-nitrophenyl) carbamoyl chloride; NMIA, N-methylindoxyl acetate; OP, organophosphate; PAS, peripheral anionic site.
The physiological, toxicological, and pharmacological importance of cholinesterases (ChEs) acetylcholinesterase (AChE; EC 3.1.1.7) and butyrylcholinesterase (BuChE; EC 3.1.1.8) has long been recognized [1-4]. Extensive work has been done on the catalytic behavior and mechanisms of these enzymes under steady-state conditions [5-7] and on the relationships between structure, dynamics, and catalytic activity [8, 9]. However, relatively few studies have been performed on pre-steady-state kinetics of ChEs.
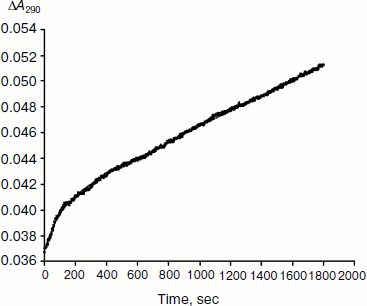
In the past years, we reported that both BuChE and AChE display a hysteretic behavior for hydrolysis N-methylindoxyl acetate (NMIA) [10, 11]. Hysteresis in enzyme catalysis can be defined as a retardation in the reaction rate upon a change in substrate (or inhibitor) concentration. Hysteresis with NMIA is characterized by a lag of several minutes during the approach to steady state. With an acetanilide substrate, 3-(acetamido) N,N,N-trimethylanilinium (ATMA), the pre-steady-state phase is a burst over several minutes [12]. These pre-steady-state behaviors were interpreted as being the result of a slow equilibrium between two enzyme forms, E and E′, having different catalytic activity towards these substrates. Kinetic cooperativity with long lag or burst phase in the approach to steady-state reflects time-dependent conformational changes; it is the characteristic of hysteretic enzymes [13-15]. Long induction times observed with hysteretic enzymes must not, therefore, be mistaken for Michaelis–Menten induction periods – of the order of microseconds or less – needed for formation of enzyme substrate complex ES (see Appendix).
Further, we showed that wild-type human BuChE and certain of its mutants displayed hysteretic behavior for hydrolysis of butyrylthiocholine (BuSCh) and benzoylcholine (BzCh) [16]. Hysteresis of human and rat BuChE with BzCh as a substrate was even more complex, showing damped oscillations that superimpose on the pre-steady-state lag phase [17, 18]. Complex time-dependent behavior of ChEs was also observed for reaction of ChEs with irreversible bulky inhibitors such as the carbamylating agent N-methyl-N-(2-nitrophenyl)carbamoyl chloride (MNPCC) [19] and the cyclic organophosphate cresyl saligenin phosphate (CBDP) [20].
The hysteretic behavior of ChEs was found to depend on the enzyme itself, the chemical structure of the substrate (or the inhibitor), and the physicochemical conditions of the medium. Mechanistic models describing the hysteresis of ChEs and a hypothesis about the possible molecular mechanism of hysteresis are presented. A hypothesis about the role of ChE hysteresis in protection of the cholinergic system against toxic substances is discussed.
MATERIALS AND METHODS
Enzymes. Kinetic experiments were performed using ChEs from different sources. Recombinant wild-type human BuChE and selected mutants, wild-type human AChE, and wild-type rat BuChE were expressed in CHO K1 cells and purified as described elsewhere [20-23]. Soluble forms of honeybee (Apis mellifera) AChE were purified from bee head [24]. Recombinant Drosophila melanogaster AChE was expressed in a baculovirus system and purified from the cell culture medium [25]. Bungarus fasciatus AChE was purified from krait venom [26], and mutants of this enzyme were expressed in stably transfected CHO K1 cells [27]. Horse serum BuChE was purchased from Sigma (USA).
Selected mutations in human BuChE were in the peripheral anionic site (PAS) (D70G, D70H, Y332A), in the active site gorge (A328C, E441D), in the oxyanion hole (G117H, A199E), and in the cation-binding site (E197Q). Mutated residues are involved either in substrate binding or in stabilization of transition states. Rat BuChE is similar to human BuChE, but it presents extensive modifications in the acyl-binding pocket, including the introduction of a prominent positively charged residue (L286R) [23]. Though horse and human BuChE present some differences in their primary sequence, their catalytic properties are similar. Introduction of triple mutations in the active site pocket of B. fasciatus AChE were aimed at engineering an organophosphate hydrolase activity [27].
Substrates and inhibitors. Substrates were N-methylindoxyl acetate (NMIA), butyrylthiocholine (BuSCh), benzoylcholine (BzCh), benzoylthiocholine (BzSCh), long N-alkyl chain derivatives of BzCh [18], and 3-(acetamido)-N,N,N-trimethylanilinium (ATMA). Experimental conditions of kinetic assays at different pH and 25°C are described in [10, 17]. Irreversible inhibitors were N-methyl-N-(2-nitrophenyl) carbamoyl chloride (MNPCC) [19], CBDP [20], and diisopropylfluorophosphate (DFP) [27]. Ranges of substrate and inhibitor concentrations were large. Maximum concentrations were as high as possible, being limited by the solubility of these chemicals in sodium phosphate or bis-tris buffers.
Kinetics of substrate hydrolysis. Assuming no significant substrate depletion, the reaction velocity expressed as the rate of formation of product P is described by:
d[P]/dt = vie–kt + vss(1 – e–kt). (1)
Induction times (τ), corresponding to transient lags or bursts before the steady state, can be calculated from the mono-exponential term of the integrated form of Eq. (1), i.e. Eq. (2). This equation describes the time course for product formation Pt throughout the transient phase and into steady state:
[P]t = vsst – (vss – vi)(1 – e–kt)/k, (2)
where vss is the steady-state velocity, vi the initial velocity, and k the hysteretic rate constant, i.e. the reciprocal of the induction time (τ), the apparent rate constant for the time-dependent conformational change. If (vss – vi) > 0, the transient is a lag, and if (vss – vi) < 0, the reaction displays a burst. The amplitude of lag or burst is (vss – vi)/k. When damped oscillations appear, superimposed on the lag, induction times can be estimated from the envelope of the damped oscillations.
Kinetics of irreversible inhibition. Progressive inhibition of ChEs by carbamoyl or organophosphyl esters was studied under pseudo-first-order conditions using the sampling method of Aldridge and Reiner [28]. The pseudo-first-order rate constant of inhibition was determined from the slopes of plots of log (residual activity) versus time.
OBSERVED PRE-STEADY-STATE SLOW INDUCTION PHASES
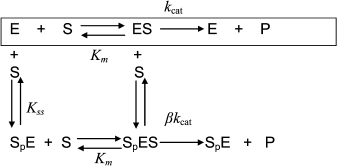
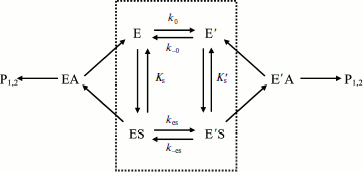
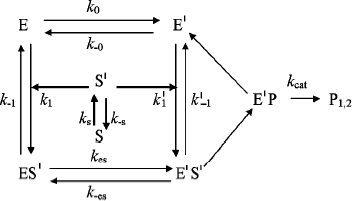
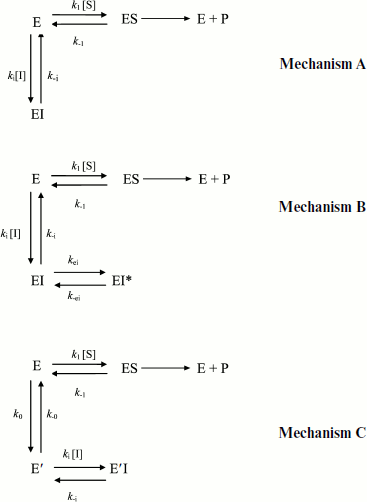
Hysteresis was seen with both neutral esters and charged esters. Kinetics of ChE-catalyzed hydrolysis of substrates can be described by Scheme 1 and Eq. (3). Therefore, the hysteretic behavior of ChEs is independent of the catalytic mechanism of substrate hydrolysis.
Scheme 1
In Eq. (3) the β factor refers to the effect on the kcat of a second substrate molecule that binds to the peripheral anionic site (PAS) to form a ternary complex SPES with a dissociation constant Kss. With neutral substrates such as NMIA that do not bind to the PAS, β = 1, ChEs displays Michaelian behavior (boxed mechanism in Scheme 1 and Scheme 10 in Appendix). Positively charged substrates, e.g. BzCh and BuSCh, bind to the PAS, and as a consequence ChEs do not display Michaelian behavior at high substrate concentration. If β > 1, there is activation by excess substrate; if β < 1, there is substrate inhibition at high [S].
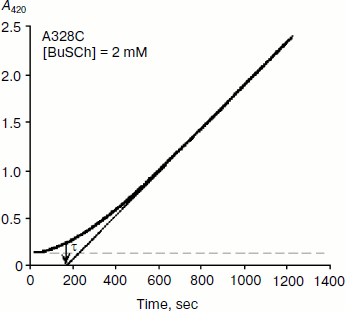
As mentioned above, hysteresis in the hydrolysis of the neutral ester NMIA by AChE and BuChE was characterized by a lag of several minutes before steady state [10]. Lags were also observed for hydrolysis of other substrates, e.g. for hydrolysis of BuSCh by the A328C mutant of human BuChE (Fig. 1). Unlike the pre-steady-state lags observed with carboxyl esters, the pre-steady-state phase for hydrolysis of the positively charged acetanilide ATMA by wild-type human BuChE and its D70G mutant showed a burst (Fig. 2) [12].
Fig. 1. Progress curve showing a lag before reaching steady state. The enzyme is the A328C mutant of human BuChE catalyzing hydrolysis of the thioester BuSCh (2 mM) in 100 mM sodium phosphate buffer, pH 7.0, at 25°C. The induction time τ = 3 min.
Type and duration of induction time depends on the substrate concentration, [S], the chemical nature of the substrate, and the enzyme (species origin and/or type of mutations). For example, for wild-type human BuChE at maximum velocity, induction time is 15 min for hydrolysis of NMIA, 3.5 min for hydrolysis of BzCh, and 100 sec for hydrolysis of ATMA. Mutations in the active center modulate induction times with a given substrate. Certain mutations can lead to hysteresis with substrates that show no observable induction time in wild-type enzyme, e.g. mutation A328C in human BuChE leads to hysteresis with BuSCh (τ = 5 min at Vmax), while wild-type human BuChE has no hysteretic behavior with this substrate. ChEs belong to the family of α/β hydrolases bearing high sequence homologies and the same folding [1, 2]. Thus, ChEs can be regarded has a family of muteins in which the invariant feature is the catalytic machinery. Hysteresis appears has an intrinsic property of ChEs and must therefore depend on one or several key residue(s) in the catalytic center.Fig. 2. Progress curve showing a burst before reaching steady state. The enzyme is the D70G mutant of human BuChE, and the substrate is the acetanilide ATMA (3 mM) in 0.1 M sodium phosphate buffer, pH 7.0, at 25°C. The induction time τ = 100 sec [12].
Theoretical analysis of the dependence of the hysteretic constant, k, on substrate concentration can be found herein [13, 29]. The dependence of the hysteretic rate constant, k (the reciprocal of induction time τ), of ChEs on substrate concentration is generally described by a downward hyperbolic function [10]. However, all kinds of dependences can be observed: upward hyperbolic dependence, e.g. for the G117H/A199E mutant of human BuChE with BzSCh [30], and A328C mutant of BuChE with NMIA; a bell-shaped dependence for wild-type BuChE with the acetanilide ATMA [12, 30]; and even k can be invariant with [S], e.g. for the D70G mutant of human BuChE with BzCh [17].
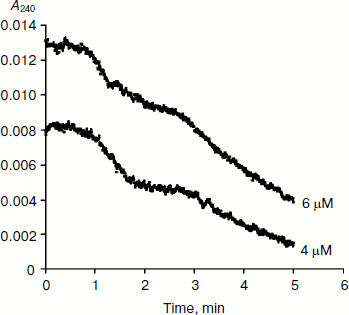
BuChE-catalyzed hydrolysis of BzCh [17] and N-alkyl derivatives of BzCh [18] show damped oscillations in the mono-exponential phase of acceleration, preceding establishment of steady state (Fig. 3). 1H-NMR spectra of substrate solutions reveal substrate conformational polymorphism. Thus, kinetic analysis of pre-steady-state phases indicates that oscillations reflect slow equilibrium between multiple conformational states of the substrate molecules, substrate oligomers, and substrate micelles. This is particularly clear for molecules such as N-alkyl derivatives of BzCh with long alkyl chains [18].
Fig. 3. Typical pre-steady-state kinetic curves showing damped oscillations. The enzyme is rat BuChE hydrolyzing an N-alkyl derivative of benzoylcholine (N-(2-benzoyloxyethyl)-alkyldimethyl ammonium bromide with n = 6 methylene units (4 and 6 µM)) in 0.1 M sodium phosphate, pH 7.0, at 25°C.
FORMAL MECHANISTIC MODELS FOR HYSTERESIS OF ChEs
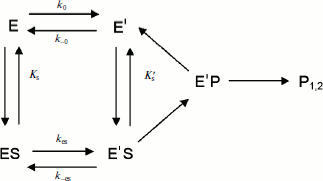
Assuming that E and E′ are two enzyme states in slow equilibrium, the general model for hysteretic enzymes established by Frieden [13] describes situations where substrate binds rapidly to both forms E and E′, and where both complexes ES and Ε′S are catalytically active and make products (P1,2) through acylation (k2) and deacylation (k3) (Scheme 2). Under these conditions, the pre-steady-state phase is characterized by either a lag or a burst depending on the relative values of the enzyme–substrate dissociation constants.
Equation (4) describes the dependence of k on [S]:
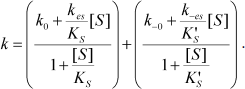 (4)
(4)
The dependence of k on [S] varies with the relative rates of the transitions E to E′ and ES to E′S. The value of k varies from k0 + k–0 at [S] = 0 to kes + k–es at high [S]. There is a negative, hyperbolic dependence on [S] if k0 + k–0 > kes + k–es. There is a positive, hyperbolic dependence on [S] if k0 + k–0 < kes + k–es. There is no dependence of k on [S] if k0 + k–0 = kes + k–es. The hysteretic behavior of the D70G BuChE mutant with BzCh [17] can be described by this latter condition. If Ks′ → , the dependence of k with [S] is described by Eq. (5):
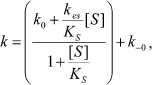 (5)
(5)
If substrate binds to E and E′ but when ES is not catalytically active, in that case vi = 0, and Scheme 2 reduces to Scheme 3. Equation (4) still describes the hysteretic rate constant for Scheme 3. Hysteresis of wild-type human BuChE with BzCh [9] corresponds to this situation. This situation occurs for the G117H/A199E mutant of human BuChE with BzSCh (vi = 0).
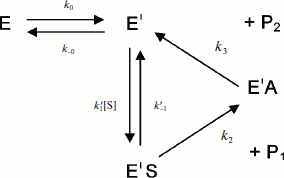
If substrate binds only to E′, the hysteretic behavior can be described by reduced Scheme 4, and Eq. (6) describes the dependence of k on [S]. If most of the resting enzyme is in the E form, then the majority of the enzyme undergoes the slow, hysteretic transition before becoming catalytically competent. Under this condition vi, the initial velocity (cf. Eq. (1)), is approximately zero. If E′ is significantly populated at time zero, vi > 0.
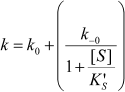 (6)
(6)
This simplest model for hysteretic behavior of enzymes (Scheme 4) describes the hysteresis of ChEs with NMIA as the substrate [7, 11]. However, this model does not explain the hysteretic behavior of BuChE with all substrates. Indeed, Eq. (6) predicts that the limiting hysteretic rate constants should be the same for all substrates. For instance, contrary to this prediction, the limiting hysteretic rate constants for hydrolysis of BzCh by wild-type human BuChE (k0 + k–0 ≈ 0.033 sec–1, k0 = 0.0048 sec–1) [17] are larger than hysteretic rate constants for NMIA (k0 + k–0 ≈ 0.003 sec–1, k0 = 0.001 sec–1) [10]. Moreover, this enzyme shows no hysteresis with BuSCh or BzSCh, and a complex dependence with certain substrates, e.g. bell-shaped dependence with ATMA [12, 30]. Therefore, the hysteretic rate constants depend on the chemical structure of the substrate.
Conversely, if substrate binds exclusively to E, and ES slowly isomerizes to Ε′S with both ES and E′S being catalytically active, then there is hysteresis in the approach to steady state. However, if E′S is inactive there is no hysteresis, but if E′S alone is active, then there is hysteresis. Such a hysteretic behavior is consistent with the model that incorporates an “induced fit” step for ChE-catalyzed hydrolysis of certain esters 21, 22. If substrate binds exclusively to E, and the transition ES to E′S is fast, then there is no hysteresis. This may explain why there is no hysteresis for hydrolysis of BuSCh and BzSCh by wild-type human BuChE. Since the transition of ES to E′S involves an enzyme–substrate complex, the rate constants for this transition may vary from substrate to substrate and/or may be different between wild type and mutants. The fact that certain human BuChE mutants, in particular A328C, show hysteresis with BuSCh supports this statement (Fig. 1).
Reaction of the acetanilide ATMA with wild-type human BuChE showed a burst in product formation. The occurrence of a burst in the approach to steady state indicates that vi > vss in Eq. (2). Three mechanisms can explain this situation: a) accumulation of an intermediate during the first turnover of the enzyme; b) slow release of hydrolysis products P; c) slow equilibrium between enzyme forms. Actually, because ATMA is a poor substrate (kcat = 140 min–1 and low kcat/Km = 12.5·103 M–1·sec–1 [12]), the burst reflects a slow deacylation step. The acetyl intermediate, EA, and the deacylation rate constant (k3) are the same as for all acetyl esters that are good substrates, e.g. NMIA (kcat = 300 sec–1). Thus, because of structural constraints imposed by the planar geometry of the acetanilide substrate, and because the energy needed for breaking the amide bond of ATMA is higher than for an ester bond, it follows that the rate-limiting step for hydrolysis of ATMA is the acylation step (k2 << k3) [12]. Therefore, the burst does not result from accumulation of the enzyme intermediate EA during the first turnover due to slow deacetylation. The observed burst phase represents the accumulation of product P from multiple turnovers of the enzyme. Therefore, the burst is due to hysteresis of the enzyme. Scheme 2 and Eq. (4) predict a hysteretic transition with a burst, leading to a slower steady state, if substrate binds to E and E′ with Ks′ < Ks, and if E′S is catalytically inactive or less productive than ES. Lastly, the dependence of the hysteretic constant, k, on [ATMA] is bell-shaped for wild-type BuChE; as said, k increase to a maximum value (k = 0.035 sec–1) at [S] = 1 mM, then decrease to the asymptotic limit (k = 0.01 sec–1) at saturating substrate concentration ([S] = 5 mM) [12, 30]. There are very few examples of pre-steady-state burst with biphasic dependence of k [31]. Scattered values of k for the D70G mutant of human BuChE make it difficult to determine the dependence of k on [ATMA] [12].
DAMPED OSCILLATIONS IN THE PRE-STEADY-STATE PHASE
Mechanistic models. As mentioned, the hysteretic behavior of BuChE showed additional complexities with BzCh and its N-alkyl-substituted derivatives [17, 18]. With these substrates, damped oscillations superimpose on the lag phase (Fig. 3). Occurrence of these oscillations was dependent on [S]. Oscillations in the progress course of enzyme reactions have been known for a long time [32]. It was theoretically predicted that any single-enzyme turnover involving two or more enzyme–substrate complexes as time-dependent variables can exhibit damped oscillations in the pre-steady-state phase [33, 34].
Damped oscillations are not predicted by the models described in Schemes 2-4. These models are based on the assumptions that the enzyme–substrate interaction is a rapid equilibrium, that [S] >> [E], with [S] essentially constant, and that transitions E/E′ and ES/ES′ are slow equilibria. These macroscopic kinetic models predict single exponential time dependence for the transient approach to steady state of enzymes in solution. However, if substrate binds exclusively to E′, the simplest hysteretic model (Scheme 4) can theoretically lead to oscillations. Goldstein established that the condition for oscillations in this model is that all the steps along the cycle E′ → E′S → E′P → E′ are irreversible, and corresponding kinetic constants are equal, k1[S] = k2 = k3 = k [35]. Then, the solution of kinetic equations for Scheme 4 is:
![]() (7)
(7)
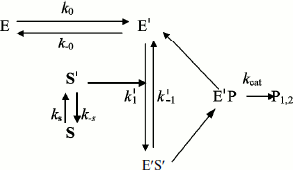
In general, substrate molecules in solution exist in multiple conformations with only one of them being capable of binding efficiently to the enzyme. Normally, transition between substrate conformations is very fast, but a slow transition from an unsuitable conformation or physical state (S) to a suitable one (S′) would constitute a slow introduction of the substrate into the reaction path. Therefore, we modified Schemes 3 and 4 as shown in Schemes 5 and 6 to include a slow change in substrate conformational/physical state. The models in these Schemes are based to the infusion models [36-40]; they include the openness condition for substrate and product, and the presence of more than one enzyme form, E and E′, that can bind substrate. The substrate concentration, [S], is assumed to be in excess so that there is no significant depletion throughout the time course. The S′ form of the substrate is assumed to be a minor fraction, [S′], of the total substrate concentration in the bulk solution, [S]. The rate of appearance of [S′] in the reaction is controlled by the “feeding” rate constant ks = kin.
In Scheme 5, S′ binds only to E′. The differential equations corresponding to Scheme 5 for the three independent concentration variables are:
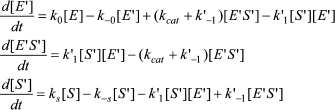 (8)
(8)
![]() (9)
(9)
In Scheme 6, S′ binds to both enzyme states, E and E′.
The differential equations corresponding to the four independent concentration variables in Scheme 6 are:
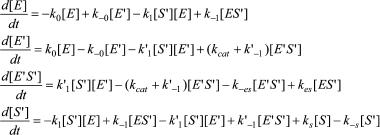 (10)
(10)
![]() (11)
(11)
To summarize, the main requirements for damped oscillations are: a) k0 must be sufficiently slow; b) S′ is produced at a slow rate (ks), and c) k–s < 0.05 sec–1. In earlier studies, Roussel stated that ks[S] has to be less than the turnover capacity kcat[E] [36]. Moreover, models predict that oscillations are favored if enzyme–substrate complex formation is irreversible. The existence of several enzyme–substrate complexes formed along the descent of substrate to its final position on the active site [21, 22] would thus favor damped oscillations. Lastly, the oscillation period was found to change slightly over the time course [17, 18] (Fig. 3). This may occur if [S] changes slowly with time. Indeed, simulations of Scheme 5 and 6 show that the damping factor and the oscillation period can be modulated by tuning the different rate constants, and by introducing multiple slow equilibria between different substrate states S S′ S′′… . Each substrate state is considered to have a different local concentration.
Multiple transitions between S and S′. The physical description of the different substrate populations and the nature of the transitions between them were important experimental issues. It is noteworthy that organic molecules in solution normally exist in different conformational states and can form clusters or aggregates, depending on concentration. Spectroscopic methods and molecular mechanics studies showed that acetylcholine in solution exists as seven populations of conformers, all of which are in rapid equilibrium, with rate constants in the picosecond range [41]. Conformers can be extended, or cyclic. Cyclic conformers are stabilized by interactions between the cationic head and the carbonyl oxygen. The preference of AChE is for the fully extended conformer. BzCh and its N-alkyl derivatives are expected to show conformational polymorphism similar to that of acetylcholine; and BuChEs are expected to preferentially bind the extended conformation of BzCh and its derivatives. But if interconversion between conformers is fast, conformational polymorphism does not support the condition of a slow feeding rate for S′ as stated in Schemes 5 and 6. However, 1H-NMR spectroscopy showed that a slow equilibrium between two populations of BzCh conformers exists in solution. A population of extended forms (I) and a population of cyclic forms (II) are in slow equilibrium (k = ks + k–s < 200-250 sec–1 and k–s >> ks) [17]. The extended form S′ (considered to be a sub-population of form I) that binds to human BuChE is thus generated at a slow rate. For N-alkyl derivatives of BzCh, slow equilibria amongst multiple conformers and substrate aggregates were also detected by 1H-NMR. Aggregation of N-alkyl BzCh derivatives leads to micelle formation around a critical concentration [18].
HYSTERESIS AND NON-LINEAR TEMPERATURE DEPENDENCE OF ChE-CATALYZED
REACTIONS
Numerous reports have shown curvatures or discontinuities in Arrhenius plots of ChEs-catalyzed reactions between 16-27°C, depending on the type of enzyme and medium conditions [42-44]. Anomalous temperature dependence of enzyme-catalyzed reactions has been known for decades [45, 46]. There are four possible causes for non-linear Arrhenius plots: a) phase transition of water at protein/solvent interfaces or of associated lipids [47]; b) convexity can be due to change in the rate-limiting step [47, 48]; c) a change in the specific heat capacity, ΔCp, of reactant(s) that affects either acylation (k2) or deacylation (k3) [49]; d) temperature-induced conformational change that precedes the rate-limiting step can cause sharp breaks in Arrhenius plots [47, 49-52]. In that later case, the temperature dependence of kcat is:
![]() (12)
(12)
Continuous convexity in AChE-catalyzed hydrolysis of substrates has been attributed to change in the rate-limiting step because acylation (k2) and deacylation (k3) are of the same order of magnitude [53, 54]. This change can be a temperature-induced conformational rearrangement of the active site. Thus, clear breaks have been first attributed to a phase transition of associated lipids, which in turn may alter the enzyme conformation [55-61]. However, the role of associated lipids was disproved, and discontinuities in Arrhenius plots are rather due to a temperature-induced conformational change [62-64]. Bound proteins or ligands can significantly shift the temperature of or abolish the break [65-67]. In particular, in the presence of high concentration of salt (NaCl), breaks are abolished [60, 61], as high concentration of salt was found to abolish hysteresis of human BuChE [10]. Wavelike discontinuities [68, 69] may thus reflects coexistence of two active enzyme forms in a narrow temperature interval around 18°C, and convexity can reflect a continuous shift in equilibrium between E and E′. Indeed, forms E and E′ are significantly populated at 25°C.
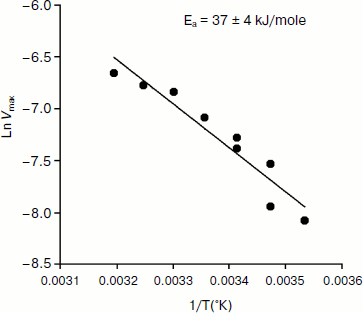
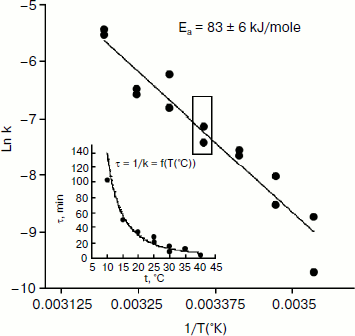
An Arrhenius plot for hydrolysis of NMIA by human BuChE was built at saturating substrate concentration (Vmax) after steady state was reached, i.e. when all the enzyme population was in the form E′. This Arrhenius plot is linear (Fig. 4). Linearity in Arrhenius plot for hydrolysis of NMIA by E′ strongly supports the contention that breaks and/or curvatures and discontinuities in Arrhenius plots for other ChE-catalyzed reactions are due to temperature sensitive slow equilibrium between the two enzyme conformational forms E and E′. In addition, the Arrhenius plot for the hysteretic constant, k, of human BuChE for hydrolysis of NMIA at Vmax is linear (Fig. 5). This suggests that the conformational change E → E′ is a two-state transition with no intermediates. Moreover, differential scanning calorimetry does not provide evidence for a change in conformational stability of ChEs around 20°C [54]. Therefore, the conformational change E → E′ must be very small and limited to the area of the active center.
Fig. 4. Arrhenius plot for hydrolysis of NMIA by human BuChE in 10 mM Bis/Tris, pH 7.0, at Vmax, i.e. saturating substrate concentration (1 mM) after steady state was reached; all the enzyme molecules are in the form E′.
Fig. 5. Arrhenius plot for the hysteretic constant, k, of human BuChE for hydrolysis of NMIA (1 mM) at Vmax in 10 mM Bis/Tris, pH 7.0.
HYSTERESIS AND PRESSURE/HEAT-INDUCED INACTIVATION OF BuChE
Eyring plots for thermal inactivation of human BuChE in both water and heavy water buffers exhibit a wavelike discontinuity over a span of 2°C around 58°C [70]. This transition was interpreted in terms of equilibrium between two temperature-dependent conformational states. Non-linear pseudo-first-order kinetics of inactivation at 60°C also suggests enzyme heterogeneity. Inactivation of human BuChE by the combined action of heat and hydrostatic pressure up to 4 kbar was found to continue after interruption of combined pressure/temperature treatment [71]. This secondary inactivation process was termed “remnant inactivation”. The occurrence of remnant inactivation or “hysteretic inactivation” following pressure/temperature pretreatment of BuChE suggests a slow conformational drift of metastable active enzyme forms toward irreversibly inactive forms.
HYSTERESIS AND INHIBITION OF ChEs
Time-dependent reversible inhibition. Time-dependent reversible inhibition of ChEs has been rarely investigated. However, it can be observed in two situations: ligand binding during affinity electrophoresis, and slow-binding inhibition in solution.
Affinity electrophoresis is a gel electrophoresis technique based on affinity of migrating proteins for ligands immobilized in the matrix. Decrease in relative electrophoretic mobility of protein as a function of immobilized ligand concentration depends on the strength of protein–ligand interaction (Kd = k–1/k1). We applied this technique to the study of the anionic site of human BuChE, using specific inhibitors (e.g. phenyl trimethyl ammonium, procainamide) entrapped in polyacrylamide gels [72, 73]. It was found that above a critical immobilized ligand concentration (L), a slow enzyme migrating form (E′) appeared and intensified at the expense of the initial enzyme form (E). This slowly migrating form was interpreted in terms of long-lived ligand-induced ChE isomerization as seen in Scheme 7.
Binding of E to immobilized ligand, L, induces a discrete isomerization of the enzyme (k3) with an increase in affinity of E′ for L, i.e. Kd′ < Kd. Because the slow form predominates at high L, it follows that the reverse reactions (k–3 and k4) E′ → E must be slow compared to the rapid association/dissociation process (k2 + k–2) of the migrating enzyme with L.
However, in light of the hysteretic catalytic behavior of ChEs, an alternative explanation can be proposed. Assuming that the enzyme exists as two forms E and E′ in slow equilibrium, the boxed model in the general Scheme 2 can account for the phenomenon observed in affinity electrophoresis of human BuChE. However, the fact that the lowest affinity form (E) is prevailing at low L would imply that k–0 > k0. Then, because Kd′ < Kd, the equilibrium is progressively shifted to E′.
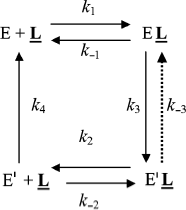
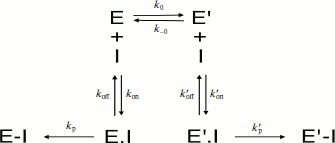
Slow-binding inhibition. Three mechanisms account for slow-binding inhibition of enzymes [74, 75] (Scheme 8): a) slow interaction (slow kon = ki) between enzyme (E) and inhibitor (I) (called “mechanism A”); b) rapid formation of enzyme–inhibitor complex (EI) followed by slow isomerization of EI to a second complex, EI* (called “mechanism B”); c) slow equilibrium between two enzyme forms E and E′, inhibitor binds rapidly to the enzyme form that does not bind the substrate (called “mechanism C”).
The kinetics of fractional enzyme inhibition by slow-binding inhibitors follows Eq. (1). Although the relations between hysteresis and slow-binding inhibition have not been thoroughly investigated, the hysteretic inhibition mechanism may involve slow conformational change of either the enzyme E or the first enzyme–inhibitor complex EI, as illustrated in Scheme 8 (mechanisms B and C). Other mechanisms for slow-binding inhibition can be considered. In particular, competition between substrate and inhibitor for both enzyme forms may theoretically occur. Accordingly, the general Frieden’s model for hysteretic enzymes (Scheme 2) can be expanded for competitive inhibition. The different mechanisms of slow-binding inhibition can be distinguished from the dependence of k, the induction constant, on inhibitor concentration [74, 75].
Kinetic analysis of slow-binding inhibition of AChE by (–)-huperzine A [76] and human BuChE shows that it obeys mechanism A in Scheme 8 (Masson et Gillon, unpublished). Slow-binding inhibition of BuChE by (+)-tubocurarine obeys mechanism B in Scheme 8 [77], and the reaction of DFP with Bungarus fasciatus AChE mutant (122HFQT125) involves also a reversible slow binding step of B type [78]. Other slow-binding inhibitors of ChEs and tight inhibitors like the protein toxin fasciculin-2 [79, 80] may interact similarly. So far the product progress curves of ChEs in the presence of slow-binding inhibitors have not been analyzed in detail, except for inhibition of Electrophorus electricus AChE by fasciculin-2 where inhibition was found to obey mechanism B [81]. There is no known reversible slow-binding inhibition of ChEs that can be described by mechanism C so far. However, we cannot rule out the possibility that certain reversible inhibitors of ChEs bind to E and/or E′ forms in slow equilibrium, thus leading to hysteresis in enzyme inhibition.
Irreversible inhibition. If the inhibitor binds and reacts irreversibly with both enzyme forms E and E′ with different bimolecular rate constants (ki > ki′) (Scheme 9), then under pseudo-first-order conditions of inhibition (E << [I]), the residual enzyme activity as a function of incubation time with the inhibitor does not follow simple first-order inhibition kinetics.
In Scheme 9, the dissociation constants of both enzyme–inhibitor complexes, E·I and E′·I, are respectively:
![]() (13)
(13)
Since [Etot]0 = [E]0 + [E′]0, the enzyme inactivation rate is:
vin = d[Etot]0/dt = kobs,app[Etot]0 = d([E]0 + [E′]0)/dt. (14)
Then, the apparent overall inactivation constant is:
![]() (15)
(15)
![]() (16)
(16)
Therefore, starting with a total activity [Etot]0 at t0, the remaining activity at time t, [Et], can be described by the sum of two pseudo-first-order processes (Eq. (17)).
![]() (17)
(17)
Such a type of inhibition was observed for carbamylation of Electrophorus electricus AChE with long-chain analogs of physostigmine [82], carbamylation of human BuChE with N-methyl-N-(2-nitrophenyl) carbamoyl chloride (MNPCC) [19], and phosphorylation of human BuChE and AChE with cresyl saligenin phosphate (CBDP) [20]. Also, reported concentration-dependent change in the apparent bimolecular rate constants (ki) of human AChE with OPs such as paraoxon [83] and chlorpyrifosoxon [84] can be explained by reaction of inhibitors with two enzymes forms, E and E′, differing in reactivity (ki > ki′) for these OPs.
MOLECULAR MECHANISM OF CHOLINESTERASE HYSTERESIS
ChEs belong to the family of αβ hydrolases, and they present strong sequence homology [1]. The fact that all studied ChEs display hysteretic behavior indicates that this behavior is an intrinsic property of this enzyme family. For example, under the same experimental conditions with NMIA as the substrate, the maximum induction time at substrate saturation is 20 min for wild-type horse BuChE [30], 16.6 min for wild-type Drosophila melanogaster AChE [11], and 2 min for wild-type Bungarus fasciatus AChE [30]. For wild-type human BuChE it is 15 min, while it is 8.5 min for the D70G mutant [10] and 4.5 min for the D70H mutant [30]. In human BuChE, residue D70 located at the rim of the active site gorge plays a role in the motion of the Ω loop that connects the PAS and the substrate binding site of the active center (Fig. 6; see color insert). Thus, sequence differences between ChEs, as well as point mutations for a given enzyme, appear to modulate induction times. However, human AChE and human BuChE that are sequentially different shows the same maximum induction time with NMIA at saturation. Then, single or multiple substitutions in the peptide sequence are not the determining factor. Though mouse AChE, human AChE, and human BuChE differ in sequence, they display the same hysteretic behavior with NMIA, i.e. τ ≈ 15 min at saturating substrate. Moreover, the fact that molecular dynamics of mouse AChE, human AChE, and human BuChE are very different [85, 86] suggests that induction time does not correlate with molecular dynamics of the enzyme.
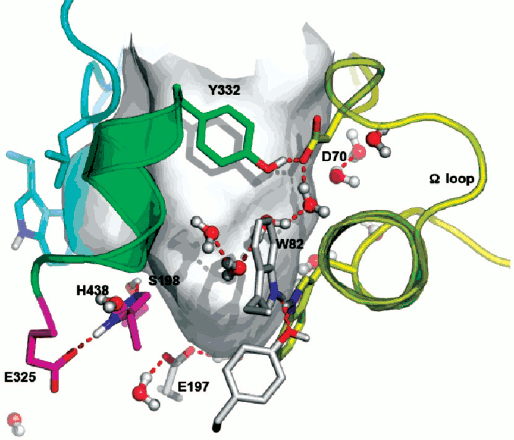
Double mutation in the oxyanion hole (G117H/A199E) of human BuChE causes hysteresis with thio-esters BuSCh and BzSCh, whereas wild-type BuChE and the simple G117H mutant are not hysteretic with these substrates [30]. With the homologous oxo-esters, BuCh and BzCh, mutated enzymes do not display this hysteretic behavior [87], and hysteresis is observed for wild-type BuChE with BzCh. It was shown that the effects on catalytic parameters (Km, acylation constant k2, and kcat) of ethereal oxygen/sulfur substitution between oxo- and thio-substrates are due to electronic and steric factors [87]. Because mutations in the oxyanion hole affect the stabilization of transition states for the chemical steps of substrate hydrolysis, the results indicate that a slight alteration in the adjustment of thio substrates in the active center at the level of acylation plays a role in the hysteretic behavior of BuChE mutated in the oxyanion hole. This implies that hysteresis of ChEs originates in the stabilization of the transition state for acylation. The fact that a mutant of human BuChE (A328C) displays hysteretic behavior with BuSCh as the substrate while wild-type BuChE does not supports this contention. In fact, molecular modeling indicates that mutated residue C328 forms a H-bond with the catalytic histidine (His438) in the resting enzyme. Thus, it may be hypothesized that hysteresis of ChEs is controlled by the conformation of the catalytic triad histidine. Induction time may depend on the probability of His438 to adopt the operative conformation in the catalytic triad. QM/MM works in progress support this hypothesis (Lushchekina et al., in preparation).Fig. 6. Active site gorge of human BuChE. Key residues are labeled: a) in the PAS (D70 and Y332); b) in the active site pocket: the π-cation binding site (W82), the catalytic triad (S198, H438, E325); c) E197 is involved in stabilization of transition states. The water molecule network interconnects key residues in the active center gorge. The Ω loop connects the PAS and the π-cation binding site. The surface in gray delimitates the solvent accessible volume of the active site gorge (500 Å3).
Water molecules appear to play a role in hysteresis. As seen on Fig. 6, key residues in the active site gorges of ChEs are interconnected via a network of structural water molecules. Perturbing the organization of water molecules was found to modulate hysteresis. In particular, it was shown that hydrostatic and osmotic pressure, temperature, chaotropic and kosmotropic salts, organic solvents, and pH affect induction time [10, 16, 17]. Hydrostatic pressure and kosmotropic salts were found to decrease induction times [4]. The hysteretic constant, k, is associated with a negative activation volume, Δ≠V0 = –45 ml/mol, indicating more structuring of water in E′ than in the unprimed form E. On the contrary, chaotropic salts [4], osmotic pressure (sugars and polysaccharides), and a water-soluble organic solvent (methoxyethanol up to 22% v/v) (Masson et al., unpublished results), that are water-structure breakers and/or act as water-suckers for sucking water molecules out of the active site gorge, caused increase in induction times. Thus, hydration of key residues by organized water molecules is important for hysteresis.
FUNCTIONNAL SIGNIFICANCE OF CHOLINESTERASE HYSTERESIS
Most hysteretic enzymes are regulatory enzymes, and it has been suggested that hysteresis may play a physiological role in damping out cellular response to rapid change in substrate or effector concentration [88, 89]. However, the actual role of hysteretic enzymes in cellular regulations has not yet been demonstrated. There is no evidence that hysteresis plays a role in function(s) of BuChE and AChE in the body. Cholinesterases, at least AChE as a regulatory enzyme, play an important role in transmission of nerve influx in the cholinergic system. Otherwise, human plasma BuChE plays a role in detoxification of poisonous esters as an endogenous stoichiometric or catalytic bioscavenger [4]. Since detoxification enzymes are promiscuous, multifunctional enzymes, they are expected to exist as conformational ensembles [90]. Therefore, physiological and/or toxicological relevance for the hysteresis of ChEs cannot be ruled out.
Hysteresis as a component of the “protein new view” paradigm. The “new view” of protein conformational dynamics proposes that proteins are normally in equilibrium between preexisting functional and non-functional conformers, and that binding of a ligand to the functional form shifts that equilibrium towards the functional conformation [91]. This conformational heterogeneity is the central concept of the “New enzymology”. This has been demonstrated for ligand binding to several enzymes, e.g. human glucokinase [92]. About ChEs, crystallographic data and MD simulations on native forms of AChE and AChE forms complexed with ligands argue for selective binding of certain ligands to preexisting conformations [93]. However, preexisting equilibrium dynamics involves a wide range of very fast motions (femtosecond-to-millisecond time scale) [94], several orders of time faster than hysteretic responses of ChEs. Thus, slow conformational dynamics of enzymes imply that the probability density to cross energy barriers is low, thus increasing waiting time for selective reactions to occur [90, 95, 96]. Our hypothesis about His438 conformation in hysteresis fits with the underlying concept of enzyme conformation landscape at the level of transition states for acylation reactions (k2) in our case.
Oscillatory hysteresis and inhibition of cholinesterases. The next question that arises is whether hysteretic mechanisms and/or oscillations of ChEs are toxicologically relevant. Could they be involved in protection of the cholinergic system during response to intoxication by reversible inhibitors or poisonous esters? Non-linear pseudo-first-order irreversible inhibition of ChEs by certain OPs and carbamates [19, 20, 82-84] suggest a damping function of hysteresis.
The functions of metabolic oscillations are scarcely understood. Potential roles for protection of cells against poisons have been proposed [97, 98], but there is no evidence that ChEs display this property even under physiological distress conditions. Yet, oscillatory behavior may occur if enzyme inhibition by excess substrate is coupled to product inhibition [99, 100]. AChE is inhibited by excess substrate [1-7], and one reaction product, H+, inhibits the enzyme. Then, it has been reported that AChE bound to bovine serum albumin (BSA) membrane at pH higher than the BSA isoelectric point (negatively charged membrane) can produce sustained oscillations in transmembrane potential upon infusion of acetylcholine (positively charged substrate) on one side of the membrane [101]. However, this observation that has never been reproduced is questionable for theoretical reasons [100]. In the case of immobilized AChE, combination of mass transfer (influx of substrate in Scheme 5) coupled to inhibition by excess substrate was found to lead to hysteresis [102]. Damping effect of mass transfer on substrate inhibition (cf. Eq. (3) with β < 1) could certainly lead to damped oscillations as in Roussel’s models [36, 37]. In addition, non-linear dynamics analysis of oscillations predicts that a substrate in-flow coupled with slow tight-binding inhibition can generate damped oscillations in an open enzyme system [103]. Because of the slow formation of EI, more ES is initially formed than the steady state allows, then oscillations occur. Numerical solution of the model equations shows that the damping is reduced, and oscillations are more likely to appear if the local enzyme concentration is high. Such a situation may prevail for BuChE on glial cell membranes and for AChE in synaptic clefts (the AChE active site density is 2500-3000 µm–2 at neuromuscular junctions [104]). Though no sustained or damped oscillations in ChE activity have been observed in vivo so far, it is therefore conceivable that such phenomena arise for membrane-bound ChEs in the cholinergic systems, and thus could play a role in short-term regulation of the cholinergic system and in its adaptive physiological response(s) to chemical aggressions.
APPENDIX
Let us consider the simple Michaelis–Menten model with two intermediates (n = 2) for hydrolysis of an ester by cholinesterases (Scheme 10), where k1 is the rate constant for formation of the enzyme–substrate complex (ES), k–1 is the rate constant for dissociation of ES, k2 is the rate constant of acylation, and k3 is the rate constant of deacylation. P1 is the alcohol product and P2 the carboxylic acid product.
Assuming [E] << [S] and k2 < k–1, with most good substrates, both acylation and deacylation are rate-limiting step: k2 ≥ k3 [87]. The Michaelis–Menten constant is:
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
Σλi = k1[S] + k–1 + k2 + k3. (21)
For hydrolysis of a substrate with a typical kcat = 333 sec–1, it follows that Σλi > 333 sec–1. Therefore, the Michaelis–Menten induction period is: τ < 1/333 = 0.8 µsec.
I thank Sofya Lushchekina (Lomonosov Moscow State University, Department of Chemistry) for her interest in this work and constant support. I am also indebted to my colleagues of IRBA-CRSSA (Marie-Therese Froment, Emilie Gillon, and Florian Nachon) and of the University of Nebraska (Larry Schopfer and Oksana Lockridge) for their participation in early experimental works.
REFERENCES
1.Massoulie, J., Pezzementi, L., Bon, S., Krejci, E.,
and Vallette, F. M. (1993) Prog. Neurobiol., 41,
31-91.
2.Taylor, P., and Radic, Z. (1994) Ann. Rev.
Pharmacol. Toxicol., 34, 281-320.
3.Massoulie, J., Perrier, N., Noureddine, H., Liang,
D., and Bon, S. (2008) Chem.-Biol. Interact., 175,
30-44.
4.Masson, P., and Lockridge, O. (2010) Arch.
Biochem. Biophys., 494, 107-120.
5.Rosenberry, T. L. (1975) Adv. Enzymol.,
43, 103-218.
6.Quinn, D. M. (1987) Chem. Rev., 87,
955-979.
7.Tougu, V. (2001) Curr. Med. Chem., 1,
155-170.
8.Silman, I., and Sussman, J. L. (2008)
Chem.-Biol. Interact., 175, 3-10.
9.Dvir, H., Silman, I., Harel, M., Rosenberry, T. L.,
and Sussman, J. L. (2010) Chem.-Biol. Interact., 187,
10-22.
10.Masson, P., Froment, M. T., Fort, S., Ribes,
F., Bec, N., Balny, C., and Schopfer, L. M. (2002) Biochim. Biophys.
Acta, 1597, 229-243.
11.Badiou, A., Froment, M. T., Fournier, D., Masson,
P., and Belzunces, L. P. (2008) Chem.-Biol. Interact.,
175, 410-412.
12.Masson, P., Froment, M. T., Gillon, E., Nachon,
F., Darvesh, S., and Schopfer, L. M. (2007) Biochim. Biophys.
Acta, 1774, 1139-1147.
13.Frieden, C. (1979) Ann. Rev. Biochem.,
48, 471-489.
14.Neet, K. E., and Ainslie, R. G. (1980) Meth.
Enzymol., 64, 192-226.
15.Kurganov, B. I., Dorozhko, A. I., Kagan, Z. S.,
and Yakovlev, V. A. (1976) J. Theor. Biol., 60,
247-269.
16.Masson, P., Froment, M. T., Nachon, F.,
Lockridge, O., and Schopfer, L. M. (2004) in Cholinesterases in the
Second Millenium: Biomolecular and Pathological Aspects (Inestrosa,
N. C., and Campos, E. O., eds.) FONDAP Biomedicine, Santiago, Chile,
pp. 191-199.
17.Masson, P., Goldstein, B. N., Debouzy, J.-C.,
Froment, M.-T., Lockridge, O., and Schopfer, L. M. (2004) Eur.
J. Biochem., 271, 220-234.
18.Hrabovska, A., Debouzy, J.-C.,
Froment, M.-T., Devinsky, Pavlikova, I., and Masson, P. (2006)
FEBS J., 273, 1185-1197.
19.Ludwig, S., Nicolet, Y., Masson, P.,
Fontecilla-Camps, J. C., Bon, S., Nachon, F., and Goeldner, M. (2003)
ChemBioChem., 4, 762-767.
20.Carletti, E., Schopfer, L. M., Colletier, J. P.,
Froment, M.-T., Nachon, F., Weik, M., Lockridge, O., and Masson,
P. (2011) Chem. Res. Toxicol., 24, 797-808.
21.Masson, P., Legrand, P., Bartels, C. F.,
Froment, M.-T., Schopfer, L. M., and Lockridge, O. (1997)
Biochemistry, 36, 2266-2277.
22.Grigoryan, H., Halebyan, G., Lefebvre, B.,
Brasme, B., and Masson, P. (2008) Biochim. Biophys. Acta,
1784, 1818-1824.
23.Ticu Boeck, A., Schopfer, L. M., and Lockridge,
O. (2002) Biochem. Pharmacol., 63, 2101-2110.
24.Badiou, A., Brunet, J. L., and Belzunces, L. P.
(2007) Arch. Insect. Biochem. Physiol., 66, 122-134.
25.Estrada-Mondaca, S., and Fournier, D. (1998)
Prot. Expr. Purif., 12, 166-172.
26.Cousin, X., Creminon, C., Grassi, J., Meflah, N.,
Cornu, G., Saliou, B., Bon, S., Massoulie, J., and Bon, C. (1996)
FEBS Lett., 387, 196-200.
27.Poyot, T., Nachon, F., Froment, M.-T.,
Loiodice, M., Wieseler, S., Schopfer, L. M., Lockridge, O., and Masson,
P. (2006) Biochim. Biophys. Acta, 1764, 1470-1478.
28.Aldridge, W. N., and Reiner, E. (1969)
Biochem. J., 115, 147-162.
29.Loudon, G. M., and Koshland, D. E. (1971)
Biochemistry, 11, 229-241.
30.Masson, P., Schopfer, L. M., Froment, M. T.,
Debouzy, J. C., Nachon, F., Gillon, E., Lockridge, O., Hrabovska, A.,
and Goldstein, B. N. (2005) Chem.-Biol. Interact.,
157/158, 143-152.
31.Cheron, G., Noat, G., and Ricard, J. (1990)
Biochem. J., 269, 389-392.
32.Hess, B., and Boiteux, A. (1971) Ann. Rev.
Biochem., 40, 237-258.
33.Ouellet, L., and Laidler, K. J. (1956) Can. J.
Chem., 34, 146-150.
34.Strickland, E. H., and Ackerman, E. (1966)
Nature, 209, 405-406.
35.Goldstein, B. N. (1983) J. Theor.
Biol., 103, 247-264.
36.Roussel, M. R. (1998) J. Theor. Biol.,
195, 233-244.
37.Davis, K. L., and Roussel, M. (2005) FEBS
J., 273, 84-95.
38.Goldstein, B. N., Aksirov, A. M., and
Zakrjevskaya, D. T. (2007) Biofizika, 52, 515-520.
39.Goldstein, B. (2007) Biophys. Chem.,
125, 314-319.
40.Goldstein, B. N., Aksirov, A. M., and
Zakrjevskaya, D. T. (2009) Biophys. Chem., 145,
111-115.
41.Vistoli, G., Pedretti, A., Villa, L., and Testa,
B. (2002) J. Am. Chem. Soc., 124, 7472-7480.
42.Baldwin, J., and Hochachka, P. W. (1970)
Biochem. J., 116, 883-887.
43.Wang, I.-C., and Braid, P. E. (1977) Biochim.
Biophys. Acta, 481, 515-525.
44.Dave, K. R., Syal, A. R., and Katyare, S. S.
(2000) Z. Naturforsch., 55c, 100-108.
45.Talsky, G. (1971) Angew. Chem. Int. Edit.,
8, 434-548.
46.Kubo, K. (1985) J. Theor. Biol.,
115, 551-569.
47.Londesborough, J. (1980) Eur. J. Biochem.,
105, 211-215.
48.Bobofchak, K. M., Pineda, A. O., Mathews, F. S.,
and Di Cera, E. (2005) J. Biol. Chem., 280,
25644-25650.
49.Fan, Y.-X., McPhie, P., and Miles, E. W. (2000)
Biochemistry, 39, 4692-4703.
50.Kayne, F. J., and Suelter, C. H. (1965)
Biochemistry, 87, 897-900.
51.Massey, V., Curti, B., and Ganther, H. (1966)
J. Biol. Chem., 241, 2347-2357.
52.Truhlar, D. G., and Kohen, A. (2001) Proc.
Natl. Acad. Sci. USA, 98, 848-851.
53.Wilson, I. B., and Cabib, E. (1956) J. Am.
Chem. Soc., 78, 202-207.
54.Oakes, J., Nguyen, T., and Britt, M. B. (2003)
Prot. Pept. Lett., 10, 321-324.
55.Plummer, D. T., Reavill, C. A., and McIntosh, H.
C. H. S. (1975) Croat. Chem. Acta, 47, 211-233.
56.Roufogalis, B. D., and Beauregard, G. (1979)
Mol. Pharmacol., 16, 189-195.
57.Nemat-Gorgani, M., and Meisami, E. (1979) J.
Neurochem., 32, 1027-1032.
58.Tsakiris, S. (1985) Z. Naturforsch.,
40c, 97-101.
59.Munoz-Delgado, E., and Vidal, C. J. (1986)
Biochem. Int., 12, 291-302.
60.Wong, R. K. M., Nichol, C. P., Sekar, M. C.,
and Roufogalis, B. D. (1987) Biochem. Cell. Biol., 65,
8-18.
61.Puterman, M. L., Hrboticky, N., and Innis, M.
(1988) Anal. Biochem., 170, 409-420.
62.Barton, P. L., Futerman, A. H., and Silman, I.
(1985) Biochem. J., 231, 237-240.
63.Vidal, C. J., Chai, M. S. Y., and Plummer, D. T.
(1987) Neurochem. Int., 11, 135-141.
64.Spinedi, A., Rufini, S., Luly, P., and Farias, R.
N. (1988) Biochem. J., 255, 547-551.
65.Axelson, S., Yong, H. X., and Karlsson, E. (1990)
J. Vet. Med. B., 37, 668-673.
66.Sindhuphak, R., Karlsson, E., Conradi, S., and
Ronnevi, L.-O. (2002) J. Neurol. Sci., 86, 195-202.
67.Al-Jafari, A. (1992) Drug. Chem. Toxicol.,
15, 295-312.
68.Roufogalis, B. D., Quist, E. E., and Wickson, V.
M. (1973) Biochim. Biophys. Acta, 321, 536-545.
69.Masson, P., Adkins, S., Gouet, P., and Lockridge,
O. (1993) J. Biol. Chem., 268, 14329-14341.
70.Masson, P., and Laurentie, M. (1988)
Biochim. Biophys. Acta, 957, 111-121.
71.Weingand-Ziade, A., Ribes, F., Renault, F., and
Masson, P. (2001) Biochem. J., 356, 487-493.
72.Masson, P., Privat de Garilhe, A., and Burnat, P.
(1982) Biochim. Biophys. Acta, 701, 269-284.
73.Masson, P. (1991) Cell. Mol. Neurobiol.,
11, 173-189.
74.Duggleby, R. G., Attwood, P. V., Wallace, J. C.,
and Keech, D. B. (1982) Biochemistry, 21, 3364-3370.
75.Morrison, J. F., and Stone, S. R. (1985)
Comments Mol. Cell. Biophys., 2, 347-368.
76.Ashani, Y., Grunwald, J., Kronmman, C., Velan,
B., and Shafferman, A. (1994) Mol. Pharmacol., 45,
555-560.
77.Stojan, J., and Pavlic, M. R. (1991) Biochim.
Biophys. Acta, 1079, 96-102.
78.Poyot, T., Nachon, F., Froment, M.-T.,
Loiodice, M., Wieseler, S., Schopfer, L. M., Lockridge, O., and Masson,
P. (2006) Biochim. Biophys. Acta, 1764, 1470-1478.
79.Easterman, J., Wilson, E. J., Cervenansky, C.,
and Rosenberry, T. L. (1995) J. Biol. Chem., 270,
19694-19701.
80.Radic, Z., and Taylor, P. (2001) J. Biol.
Chem., 276, 4622-4633.
81.Golicnik, M., and Stojan, J. (2002) Biochim.
Biophys. Acta, 1597, 164-172.
82.Perola, E., Cellai, L., Lamba, D., Filocamo, L.,
and Brufani, M. (1997) Biochim. Biophys. Acta, 1343,
41-50.
83.Rosenfeld, C. A., and Sultatos, L. G. (2006)
Toxicol. Sci., 90, 460-469.
84.Shenouda, J., Green, P., and Sultatos, L. (2009)
Toxicol. Appl. Pharmacol., 241, 135-142.
85.Carletti, E., Colletier, J.-P., Dupeux, F.,
Trovaslet, M., Masson, P., and Nachon, F. (2010) J. Med. Chem.,
53, 4002-4008.
86.Peters, J., Trapp, M., Hill, F., Royer, E.,
Gabel, F., Trovaslet, M., Nachon, F., van Eijck, L., Masson, P., and
Tehei, M. (2012) Phys. Chem. Chem. Phys., 14,
6764-6770.
87.Masson, P., Froment, M. T., Gillon, E., Nachon,
F., Lockridge, O., and Schopfer, L. M. (2007) Biochim. Biophys.
Acta, 1774, 16-34.
88.Neet, K. E., and Ainslie, G. G. (1980) Meth.
Enzymol., 64, 192-227.
89.Icimoto, M. Y., Barros, N. M., Ferreira, J. C.,
Marcondes, M. F., Andrade, D., Machado, M. F., Juliano, M. A., Judice,
W. A., Juliano, L., and Oliveira, V. (2011) PlosOne, 6,
e24545 (1-7).
90.Atkins, W., and Qian, H. (2011)
Biochemistry, 50, 3866-3872.
91.James, L. C., and Tawfik, D. S. (2003) Trends
Biochem. Sci., 28, 361-368.
92.Kim, Y., Kalinowski, S. S., and Marcinkeviciene,
J. (2007) Biochemistry, 46, 1423-1431.
93.Xu, Y., Colletier, J. Ph., Jiang, H., Silman, I.,
Sussman, J. L., and Weik, M. (2008) Prot. Sci., 17,
601-605.
94.Ramanathan, A., Savol, A. J., Langmead, C.,
Agarwal, P. K., and Chennubotla, C. S. (2011) PlosOne, 6,
e15827 (116).
95.English, B. P., Min, W., van Oijen, A. M., Lee,
K. T., Luo, G., Sun, H., Cherayil, B., Kou, S. C., and Xie, X. S.
(2006) Nature Chem. Biol., 2, 87-94.
96.Benkovic, S. J., Hammes, G. G., and
Hammes-Schiffer, S. (2008) Biochemistry, 47,
3317-3321.
97.Hauser, M. J. B., Kummer, U., Larse, A. Z., and
Olsen, L. F. (2001) Faraday Discuss., 120, 215-227.
98.Olsen, L. F., Hauser, M. J. B., and Kummer, U.
(2003) Eur. J. Biochem., 270, 2796-2804.
99.Shen, P., and Larter, R. (1994) Biophys.
J., 67, 1414-1428.
100.Bayramov, Sh. K. (2002) Fizika,
8, 6-9.
101.Friboulet, A., and Thomas, D. (1982)
Biophys. Chem., 16, 153-157.
102.Malik, F., and Stefuca, V. (2002) Chem.
Pap., 56, 406-411.
103.Ngo, L. G., and Roussel, M. R. (1997) Eur.
J. Biochem., 245, 182-190.
104.Anglister, L., Eichler, J., Szabo, M.,
Haesaert, B., and Salpeter, M. M. (1998) J. Neurosci. Meth.,
81, 63-71.
105.Maguire, R. J., Hijazi, N. H., and Laidler, K.
J. (1974) Biochim. Biophys. Acta, 341, 1-14.