Article

Age Fluctuations in Mortality of Mice with Mutation Causing Growth Retardation

A. G. Malygin

Bach Institute of Biochemistry, Russian Academy of Sciences, Leninsky pr. 33/2, 119071 Moscow, Russia; E-mail: agmalygin@mail.ru

Received May 17, 2013
Lifespan of mice over a number of consecutive generations of descendants of a male with a mutation causing growth retardation was studied. The mutant and normally developing (normal) mice were obtained by crossbreeding of mutant males with normal females from the same brood. The mutant females were infertile. Mortality of the mutant and normal mice was shown to fluctuate depending on age. The curve of dependence of lifespan on their serial number in a series of lifespan increase (mortality rank curve) had the form of evident steps for the mutant mice, while in normal mice this feature was less pronounced. These steps indicate that in the course of development of mice stages with low mortality are alternately replaced by stages with increased mortality. One month after birth, the first stage of stable development of mutant males and females is replaced by a stage with abnormally high mortality, which coincides with the period of their maximal backlog in weight compared to the normal animals. Within two months, surviving mutants catch up in weight with normally developing mice and externally become indistinguishable from them. The steps are reproduced on mortality rank curves in mutant and normal mice, both in groups of mice of different sexes and in parallel same-sex groups. The observed phenomenon is interpreted within the hypothesis of a genetic aging program in mice that provides periodic changes when stages of great viability are followed by stages of increased sensitivity to the external risk factors causing death. Less-expressed steps on mortality rank curves of normal females were shown to be enhanced by the removal from the sample of parous females and animals with tumors. Results of the study indicate the possibility of detecting in humans of ontogenesis-programmed stages of high and low sensitivity to external influences and the prospect of the development of effective measures to prevent risks of premature death.
KEY WORDS: lifespan, mice, growth retardation, development stages, mortality intensity, Gompertz–Makeham equation
DOI: 10.1134/S0006297913090095

All biological and medical researches in one way or another try to achieve extension of lifespan. Since the processes taking place in living organisms are very complicated compared to the phenomena of inanimate nature, many biologists, being guided by the principle “from simple to complex”, see the key to life extension in discovering the secrets of its origin. However, the long search for mechanisms of life origin has not been successful. Even if biologists managed to recreate a living cell, it would still be unclear how that can accelerate the search for ways of extending human lifespan.

Therefore, an attempt to approach this task from the opposite direction, namely through the study of death mechanisms, seems to be more promising. In contrast to the elusive spontaneous birth of life, the phenomenon of death is available for direct observation, and the development of effective methods of its reversal (reanimation) leads directly to the goal. The famous French physiologist Claude Bernard, one of the founders of thanatology (the science of death), wrote in his Lectures on Experimental Pathology [1]: “…in order to know how human and animal organisms live, one needs to see how they die, for life mechanisms can be discovered and understood only through understanding mechanisms of death”. In addition, we can quote the words of I. P. Pavlov: “…what a vast and fruitful field for physiological research would have opened, if immediately after diagnosing the disease or facing the imminent death, a competent experimenter would look for the ways to win over one and the other” [2].

However, thanatology is currently so unpopular among biologists, that, as appears from survey, many of them do not even know the term. Meanwhile, medicine faces the problem of discovering the immediate causes of death. After autopsy, pathologists often name the incompatibility of the state of various tissues or organs with life as the cause of death. However, in the case of people who die from accidents, the state of tissues and organs sometimes proves to be such that, according to the accepted criteria, these people should have died long ago. This paradox is quite well known, and it is even specially noted in the article “Thanatology” in the Great Medical Encyclopedia [3]. It questions the practiced methods of qualification of obvious changes in an organism as death causes and stimulates the search for other more profound causes.

Gerontology presents two opposite views on the nature of aging and death. According to one of them, processes leading to death are part of the program of development of the organism [4]. Another approach states that it is accumulation of damages caused by random (stochastic) impacts of the environment that causes aging and death [5]. Supporters of each view come up with incontrovertible arguments in favor of their theory. Theoretical justification of the first position assumes aging and death to be the same type of genetically programmed time phases of development as growth, puberty, childbearing, and others. Many phenomena are used as examples illustrating this approach: programmed death of some plants after flowering and fruiting, of ephemeral butterflies after egg-laying, of salmons after spawning, etc. However, there also exists compelling justification of the second position: dependence of aging and death on accidentally acquired diseases, systematic effects of toxic substances, ionizing radiation, and other unfavorable conditions of the environment.

However, all the arguments in favor of one position are not sufficient to refute the opposite position. Hence, the issue can be resolved only within a new concept that would unify the two approaches.

Difficulties in identifying the real causes of aging and death are also related to the fact that the very concept of cause is ambiguous, since any cause is the consequence of another cause. In the simplest case, the chain of cause–effect dependence is linear, but often it can be branched because the effect may be the result of coincidence of two or more causes.

Search for cause–effect dependences usually involves a demonstration of the reversibility of a given phenomenon after elimination of its cause. Difficulties in reversing the phenomenon of death indicate that attempts for revival do not take into account all the reasons leading to death.

The assumption of death being the result of coincidence of some programmed critical stages of organism development and unfavorable external influences may be a prerequisite for the successful resolution of the described opposition between the two understandings of the nature of aging and death.

Discovery of regular inhomogeneities on the statistical curves of natural mortality in human and animal populations might prove that entering the programmed critical development stages is one of the causes of an organism’s death. However, as the search for such irregularities is very time consuming and requires many years of observation, statistical regularities of mortality have not yet been sufficiently studied. For example, it is difficult to explain the fact that statistics of the data on general mortality and mortality resulting from specific diseases such as hypertension, hernia, tumors, etc. are described by the same Gompertz curve [6, 7]. This might mean that either these diseases are not the true causes of death or there is an underlying cause that is responsible for both the development of each of those diseases and for general mortality [8].

In this work we have studied the statistics of the natural death of mice with a randomly obtained mutation causing growth retardation and of mice with normal development. The discovery of a stage of increased mortality in the initial period of development of the mutants became our reason for a critical approach to the description of mortality dynamics within the standard Gompertz–Makeham model [9]. Lifespans of mutant and normally developing (normal) mice were traced to determine the suitability of this model in our case. On the other hand, the literature presents numerous data on midget animals whose lifespan often exceeds that of normal animals [10], and these data encourage studies of the lifespan of mutant mice who have survived the first critical stage of development. The advantage of this approach is that the conclusions on the nature of death are based on studying the statistics of the undeniable fact of death, and not on the observations of physiological processes accompanying death.

The purpose of this study was to confirm previously obtained results [11, 12] on the discrepancy between experimental and theoretically calculated (according to the Gompertz–Makeham model) dependences of mutant mouse lifespans on their rank distribution in lifespan (mortality rank curves). We also wanted to demonstrate on the newly obtained material the age fluctuations of mortality in mutant and normal mice and use it as the basis for conclusions on the possibility of reconciling the two contrasting understandings of the nature of aging and death through the development of a general concept.

MATERIALS AND METHODS

We used offspring of mice obtained by crossbreeding of a normal female from a heterogeneous laboratory population with admixture of Swiss Webster line from the “Andreevka” vivarium of the Research Center for Biomedical Technologies, Russian Academy of Medical Sciences, and a mutant male with growth retardation. The mutant male was accidentally discovered in the offspring of a normal male of the same line that had been given 0.01 M AgNO₃solution for 1.5 months from 28 days of age, and one month after the end of this treatment was crossbred with an intact female of the same line. The mice were kept in the vivarium on a standard laboratory chow balanced in proteins, fats, and carbohydrates, with all the necessary vitamins and microelements.

Data on birth, death, and lifespan of mice were accumulated for over 5 years. These data are presented in the table (see Supplement to this paper on the site of the journal http://protein.bio.msu.ru/biokhimiya) in order of birth dates and are divided into four groups of mice: mutant males, mutant females, normal males, and normal females. The lifespans of the mice were determined by the difference between the dates of their birth and natural death. The graphs are based on the data from the table. The graphs and their transformation were obtained using the Origin computer program.

Табл. S1RESULTS AND DISCUSSION

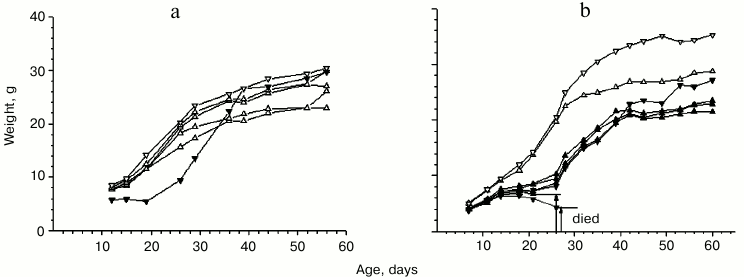
General characteristic of mice with growth-retarding mutation. Changes in weight of the initial mutant male mouse and normally developing (normal) mice from the same brood during their growth are presented in Fig. 1a. Mutant females with growth retardation, when crossbred with either mutant or normal males, were shown to produce no progeny or gave birth to pups who died within one or two days. Therefore, the mutation was passed on to the next generations only through the crossbreeding of mutant males and normal females. In broods derived from the crossbreeding of mutant males and normal females, the number of mutant individuals varied widely and was represented by both genders (see Fig. 1b for an example). The total number of mutants in broods was about 30%. On one hand, this indicates the non-recessive nature of the mutation, but on the other hand it is not sufficient to consider this mutation to be dominant. The mutation might be assumed to have some epigenetic character.

Fig. 1. Weight changes in mutant and normal mice in the initial period of ontogenesis. Broods: a) with one normal male, three normal females, and one mutant male – the ancestor of the entire population (date of birth – 08.07.07); b) with one normal male and one normal female, two mutant males, one of which died at the age of 27 days, and four mutant females, one of which died at the age of 26 days (date of birth – 11.02.10). Light down-pointed and up-pointed triangles represent normal males and females, respectively. Dark down-pointed and up-pointed triangles represent mutant males and females, respectively.

Comparison of the weight changes in mutants and normally developing animals showed mutants to lag behind in growth only during the first two months of development. As can be seen in the graphs in Fig. 1, the maximal weight difference between mutant and normal mice can be observed approximately one month after birth. In most cases the weight of the mutants ceases to increase or even start to decrease by the middle of the first month. It should be also noted that the period of suppression of mutant development corresponds to the period of rapid weight gain on the growth curve of normally developing mice (between days 15 and 30 after birth).

There was one fact that proved to be most important for our research: some mutants were unable to overcome the period of growth retardation and died at the age of 25-35 days (Fig. 1b). It is difficult to come up with a univocal explanation of the causes of their death. However, in the 1950s this age was shown to have maximum sensitivity to ionizing radiation in normal mice (Fig. S1; see Supplement) [13]. It was also found that in the case of a similar development stage in rabbits, heart muscle showed a maximum rate of oxygen consumption at with minimum intensity of glycolysis [14]. Increased mortality of mice at this stage can be assumed to be caused by a well-known effect in radiobiology – the enhancement of the harmful effect of ionizing radiation by the increase in oxygen concentration in tissues. That is, the deaths of mice were caused by the concurrence of internal or external causes, namely, genetically programmed metabolic changes with time and exposure to ionizing radiation. It can be assumed that the observed mutation of growth retardation can lower the threshold of sensitivity to the safe for normal animals background effect of unknown nature, the results of which are similar to those of ionizing radiation.

Comparison of the curves of weight gain of mice and that of humans (the latter was obtained in the first half of the last century by Schmalhausen [15]) shows that the area of rapid weight gain on the mouse curve (15-30 days) corresponds to the area of rapid weight gain on the human curves (12-19 years). At the same time, the maximum at the initial part of the curve of the logarithm of human mortality (Fig. S2; see Supplement) [7], which is not described by the Gompertz–Makeham equation, corresponds to 20 years, which is practically the same as the end of the period of rapid weight gain in humans. This fact suggests the areas of maximum death risk at the initial life period to correspond to the similar stages of development in mice and humans.

Alternative method for graphical presentation of data on mortality of mice. When studying mortality statistics, gerontologists usually use methodology developed in demography. In demographic studies, there are strong traditions regarding the ways of presenting statistical data. These traditions date back to the early nineteenth century when an employee of an insurance company, Gompertz [6], suggested using the function of mortality intensity to characterize the mortality of a population:

µ(x) = dl_m(x)/[l(x)dx].

He also showed with extensive statistical material that for people aged 35-to-90-year-old, mortality intensity can be described by an exponential dependence on the lifespan:

dl_m(x)/[l(x)dx] = Rexp(αx), (1)

where µ(x) – function of the mortality intensity; x – lifespan; l_m(x) – function of mortality – the number of people dead by this age; l(x) – function of survival – the number of people surviving to this age; dl_m(x)/dx – derivative that shows the rate of death of people of given age; R, α – values of parameters characteristic for the studied population.

Functions of mortality (not to be confused with the function of mortality intensity) and survival complement each other and are connected by the relation:

l(x) = l₀ – l_m(x), (2)

where l₀ – the total number of deceased and surviving individuals.

The Gompertz function has been widely adopted in demographic studies as it allows using only two parameters when describing mortality, and its logarithm gives a straight line:

lnµ(x) = αx + R. (3)

Initial statistical data are smoothed before differentiation by averaging over the same time periods to reduce the spread of points on the experimental curve of the mortality intensity.

Unlike humans, data on mortality in small homogenous populations of laboratory animals sometimes cannot be described by straight lines according to Eq. (3) of the Gompertz model [16]. It is often impossible to match experimental data with the straight line even after using the smoothing procedure. One example of this can be found in the book by M. Lamb, where the author presents experimental curves of mortality intensity of humans and drosophila (Fig. S2 in Supplement) [7]. Moreover, even in the case of humans, the logarithmic form of the experimental curve of mortality intensity in the range up to 30 years has a sinuous form. There are reliable data indicating a similar phenomenon for ages older than 90 years. In particular, in book of L. A. Gavrilov and N. S. Gavrilova [8] one can find the logarithm of the intensity of Swedish male mortality in the range from 85 to 105 years, which has bends at 97 and 100 years and a maximum at the age of 104 years [17]. Figure S3 (see Supplement) shows a similar curve for women from 13 Western European countries and Japan who were 80-122 years of age [18].

However, wave-like fluctuations of mortality intensity in older people are poorly studied, and they are usually not associated with similar fluctuations at earlier ages. Demographers usually ignore deviations of the statistical curve of mortality intensity from the theoretical curve in its initial and final sections. This habit can be explained by the fact that the total share of death cases (excluding deaths during the first year of life) in these sections of the experimental curve does not exceed 3% of total mortality. In contrast to demographers, gerontologists, who view death as the completion of aging, should be interested in detailed research on the bends in experimental curves of mortality intensity. However, the observed deviations of experimental values from theoretical curves are still considered to be accidental, and professionals are rarely interested in them.

In 1860, Makeham introduced the additional parameter A to formula (1) so as to lower the lower limit of applicability of the Gompertz function to the age of 25 years [9]:

dl_m(x)/[l(x)dx] = A + Rexp(αx). (4)

It would seem that the degree of compliance of the data on the lifespan of mice and the Gompertz–Makeham equation could be determined by comparing experimental curves of mortality intensity with theoretical straight lines calculated using the selected parameters A, R, and α. However, it follows from Eqs. (1) and (4) that to obtain an experimental curve of mortality intensity, it is necessary to get the derivative by numerical differentiation of the experimental mortality curve. Differentiation requires pre-smoothing of the curve by averaging the data, this procedure being justified only in the case of large amounts of raw statistical data. As the number of studied mice is rather limited in our case, it was reasonable to check the correspondence between experimentally obtained data and those predicted by theory by direct comparing of the experimental and theoretical mortality curves. The function describing the theoretical mortality curve follows the equation:

l_m(x) = l₀{1 – exp[(1 – exp(αx))R/α – Ax]}. (5)

This can be obtained by integrating the Gompertz–Makeham Eq. (4) at initial conditions x = 0 and l_m = 0.

In contrast to the Gompertz–Makeham function of mortality intensity, the mortality function does not contain a derivative, and therefore averaging is not required to obtain a corresponding experimental curve. However, since averaging and smoothing of data are widely used in creating mortality and survival graphs even when they are not used for creating the curves of mortality intensity, the validity of rejecting this procedure requires justification.

The procedure of data averaging is usually justified on the grounds that due to eliminating random deviations it reveals the true nature of experimental dependences. However, this argument does not seem to be valid since it is not based on objective criteria for assessing the regularity or randomness of the obtained results. It is only reproducibility for observed changes in independent experiments that can serve as a criterion of their regularity in this case. Ignoring this criterion turns averaging of experimental data into a method for simplifying information, the reverse side of which is its loss and distortion. For example, if each point on the curve is obtained by averaging ten experimental points, then the original information is reduced by ten times. At the same time, the averaged value does not represent any of the actual values obtained, and consequently, the information is distorted.

For the calculation of mortality curves of human populations, intervals of 1 or 5 years are often used. As can be seen in Fig. S2 (Supplement) [7], a five-year interval used for averaging the curve of mortality intensity in people completely eliminates discovery of any objective regularities within this interval. In the case of wave-like character of an experimental curve, averaging can eliminate fluctuations with periods longer than the intervals used for averaging. As a result, the fine structure of the experimental curve becomes fundamentally unobservable.

Averaging and smoothing were first used by astronomers for economical description of astronomical observations by simple analytical functions. This approach allowed compressing large amounts of information to a limited set of parameters within the given function. In this case, partial distortion and loss of information were consciously allowed [19]. Later these methods penetrated into other areas of science. But nowadays the problem of economical recording of scientific information is no longer valid due to availability of computers. Therefore, the use of this procedure should be excluded when there are no compelling reasons for averaging information, like for description of lifespan of a limited number of animals.

The continued commitment of demographers to averaging the data on survival and mortality curves can be explained by factors of subjective nature. In case of natural sciences, initial values of an independent variable determined by an experimenter are typically placed uniformly along the horizontal axis, while the values of a dependent variable obtained in the course of experiments are counted on the vertical axis. Demographers, by tradition, act differently.

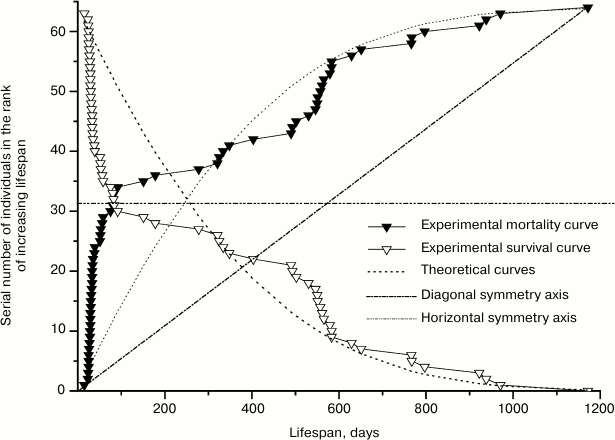
The way of presenting experimental material adopted in demographic research is shown on the example of mortality and survival curves of mutant males in Fig. 2. In accordance with Eq. (2), survival and mortality curves appear on the graph of Fig. 2 as mirror images of each other in the horizontal axis of symmetry, which passes through the value of half of the animals participating in the experiment. In these graphs, the values of a dependent variable, which correspond to the lifespans of the mice, are placed on the horizontal axis, and the values of the independent variable – the number of deceased individuals expressed in natural numbers following the increase of their lifespan – are placed along the vertical axis. As a result, experimental points are placed unevenly relative to the horizontal axis – with gaps that give the impression of a carelessly executed study. For points to be evenly distributed along the horizontal axis so as to avoid gaps, demographers use the above-discussed procedure of averaging with discrete time intervals. According to this approach, the number of deceased mice in each of the equal age intervals should be summed up and divided by the number of these values in the given interval. As a result, instead of several points each interval is represented by only one point indicating the average number of deceased mice. Consequently, the obtained dots are evenly distributed along the horizontal axis. However, equal distances between the points surpass the size of gaps, and the initial equability of their distribution along the vertical axis is lost.

Fig. 2. Experimental mortality and survival curves of 64 mutant males and respective theoretical curves calculated using Eqs. (2) and (5) for the parameter values: A = 1.0·10^–4; R = 2.3·10^–3; α = 1.2·10^–3; l₀ = 64.

Meanwhile, the desire to eliminate the gaps on the horizontal axis has no rational justification. These gaps mark the periods of development corresponding to zero mortality and, therefore, serve as a source of valuable information on the stages of maximal viability of organisms during ontogenesis.

The generally accepted way of presenting experimental data on graphs (i.e. without gaps on the horizontal axis) can be reached also without averaging of data for equal time intervals. To do this, mortality function should be converted into its opposite, rank mortality function. In the case of this function, the serial number of mice in the rank of increasing lifespan is used as an independent variable on the horizontal axis, and lifespan is used as the dependent variable describing the experimental results. As the number of mice deceased by a given age is equivalent to their serial number in the above-described rank of values of the independent variable, the transition to the new graph means only exchange between horizontal and vertical axes in the mortality graph. That is, the function of mutant males mortality l_m(x) (Fig. 2) turns into the rank function of their mortality x(l_m) (Fig. 3) by mirroring the mortality curve in the diagonal axis of symmetry. In this case the ordinates of the experimental points are distributed evenly along the horizontal axis according to the generally accepted form of making graphs. As a result, horizontal gaps on the mortality curves turn into vertical gaps of rank mortality curves. Since the number of points on the curves does not change, the conversion of a graph, in contrast to the averaging procedure, does not reduce its information content. On graphs for curves shifted to the right relative to the first curve, absolute numeration of mice is determined by the graduation of the horizontal axis with subtraction of the shifting value.

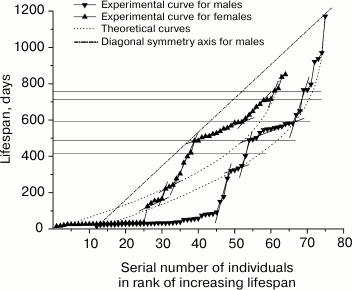
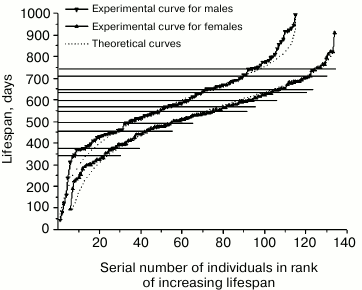
Fig. 3. Rank mortality curves of 64 mutant males (right) and 64 mutant females (left). Theoretical curves were calculated using Eq. (5) for the parameter values for males: A = 1.0·10^–4; R = 2.3·10^–3; α = 1.2·10^–3; l₀ = 64, and for females: A = 7.0·10^–4; R = 1.9·10^–3; α = 1.5·10^–3; l₀ = 64.

To compare experimental rank mortality curves with theoretical ones, we need a method of making the theoretical curves. Since the formula of rank mortality function cannot be obtained in an explicit form by algebraic changes in formula (5), the theoretical rank mortality curve was created using the Origin program by graphic changes of the theoretical curve of mortality function created using formula (5). Parameters of the Gompertz–Makeham equation were calculated using four experimental values of survival function (2) by the method described by L. A. Gavrilov and N. S. Gavrilova [8].

Patterns of mortality of mice. Figure 3 shows rank mortality curves of mutant males and females. It is evident that the theoretical curves created by using Eq. (5), following the above-described method, have no inflections, whereas a number of steps can be clearly seen on the experimental curves. Fragments of the curves with steps are approximated by straight line segments. Steep sections of steps correspond to the stages of sustainable development, while flat sections correspond to the stages of increased mortality. Steep sections include vertical gaps whose boundaries often coincide with the points of intersection of line segments approximating the steps (when the number of mice used in experiments is rather small). Intersection points of approximating line segments and the gap ends are projected on the vertical axis by horizontal lines indicating the boundaries of relevant age intervals. Age intervals corresponding to the gaps, can be considered as the areas where the risk of natural death is minimal.

Figure 3 shows that age intervals of flat areas of steps, including the highest number of deceased animals, are almost identical at the curves of mutant males and females. These intervals are: 15-39 days (24 males), 490-583 days (13 males) and, respectively, 15-36 days (24 females), 485-589 days (14 females). Close in value vertical gaps adjoin the flat areas from below: 0-15 days, 403-490 days for males and 0-15 days, 419-485 days for females. Thus, the two most expressed steps on each of the curves pairwise correspond to each other and determine similarity of the curves.

Furthermore, age intervals 150-178 days (2 males) and 124-165 days (5 females), 321-350 days (5 males) and 364-419 days (3 females), 766-797 days (3 males) and 761-775 days (2 females) can be noted. However, the presence of steps is statistically less reliable in this case because of the small number of animals in the respective fragments of the curves.

The curves differ from each other in the structure and intensity of mortality of the mice at age intervals of 178-321 days (2 males) and 165-304 days (4 females); 629-710 days (2 males) and 607-710 days (8 females). In both the first and second cases, female mortality in parallel age intervals substantially exceeds male mortality. Both curves have a steep part of the step in the age interval of 710-770 days (the gap constitutes the greater part of it).

It should be noted that gaps (in contrast to straight line segments approximating the step areas or corresponding age intervals on the vertical axis of the graph) cannot serve as stable step characteristics. This is due to the fact that as the number of animals in the experiments increases, the gaps are reduced or altogether disappear, turning into lines filled with dots in the steep step areas. Therefore the gaps are useful for small statistics of observations at the intermediate stage of research only as a criterion exposing the steps.

The following method was used to show that the deviations of experimental curves from theoretical ones created by using the parameters of Gompertz–Makeham equation are reproducible, and therefore the steps observed on experimental curves are not random.

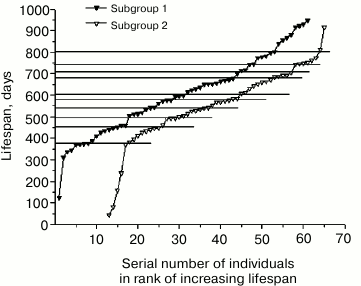
The groups of mutant males and females were placed in ranks according to the increase in the date of half of their lives. The latter values were determined by adding the date of birth and (or subtracting from the date of death) half of the individual lifespan. Then each rank was divided in half to give two equal subgroups of mice. Previously used [11, 12] arrangement according to birth dates shifted the probability of distribution of long-lived individuals in the direction of the first subgroup, and that of short-lived individuals in the direction of the second subgroup, while arranging according to death dates, on the contrary, shifted the probability of distribution of long-lived individuals in the direction of the second subgroup, and that of short-lived toward the first subgroup. Arranging of mice in ranks according to the date of half-life eliminated this asymmetry.

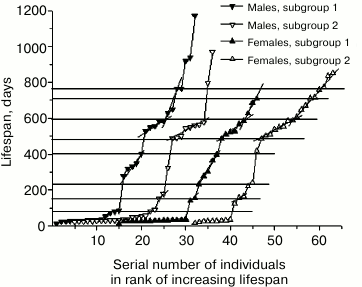
Rank mortality curves for the subgroups of mutant males and females are presented in Fig. 4. Since the curves for the parallel subgroups can be interpreted as the result of two independent experiments, similarities in the position and size of age intervals of increased mortality 25-35 days, 485-600 days and intervals of reduced mortality 80-150 days, 410-485 days, and 710-760 days on rank mortality curves of male and female subgroups suggest reproducibility of corresponding steps, that is, these steps have regular character. At the same time, increased mortality of males and females in the interval from 200 to 400 days in the first subgroups indicates the absence of full equivalence between early and late subgroups.

The observed differences can be omitted if we attribute them to coincidence related to insufficient statistics of observations. However, explanation of these differences by means of hypotheses that can be verified seems more productive. For example, these differences can be attributed to the process of stabilization of genome disbalance by the initial mutation of growth retardation, which was manifested in the first male mutant in abnormally long lifespan (1172 days). Eleven-year cycles of solar activity can also be used to explain this phenomenon. Magnetic storms are known to have significant impact on mortality, and the total time of observation of mouse mortality comprised half of the solar activity cycle in this case.

Fig. 4. Rank mortality curves for four subgroups of mutant mice obtained by dividing in half the ranks of 64 mutant males and 64 mutant females arranged by dates of their half-lives.

Figure 5 shows the rank mortality curves of normally developing males and females. These curves (in contrast to experimental rank mortality curves of mutant mice) are satisfactorily described by theoretical curves. Certain discrepancies are observed only at the ends of the curves and with respect to the fine structure of the experimental curve of males. The discrepancies at the ends of the curves are consistent with the fact that the Gompertz–Makeham equation, as seen in Figs. S2 and S3 (Supplement), also cannot describe the changes in the initial and final sections of the experimental curves of mortality intensity in human populations.

Fig. 5. Rank mortality curves of 115 normal males (top curve) and 129 normal females (bottom curve). Theoretical curves were calculated using Eq. (5) with the parameters for males: A = 1.0·10^–5; R = 9.8·10^–5; α = 6.5·10^–3; l₀ = 115, and for females: A = 1.0·10^–5; R = 1.1·10^–4; α = 7.0·10^–3; l₀ = 129.

Рис. 2When comparing Figs. 3 and 5, one can see that age intervals 460-490 days and 720-750 days of the steep parts of the steps on the rank mortality curve of normal males overlap with age intervals 410-485 days and 710-770 days of the steep parts of corresponding steps on the rank curves of mutant males and females. At the same time, the step with age interval 0-30 days, being characteristic only for mutant mice, is absent from both curves of normal mice.

Confirmation of the regular nature of deviations of the experimental curve from a theoretical one was obtained for normal males in the same manner as for mutant mice. The rank of data on the male lifespan compiled according to the increase in half-life date was divided into two parts so that corresponding age intervals of the steps of rank mortality curves for male subgroups would best align with each other in Fig. 6. As can be seen, age intervals corresponding to the steep and flat areas of steps, which are divided by points 370-460-500-540-580 days, practically completely coincide in their position and size in both curves. Intervals in the range from 600 to 680 days are slightly shifted relative to each other. Intervals at 680-710-740 days of the steep area of the steps again coincide.

Thus, repeatability of steps on the rank mortality curves for independent subgroups of normal males confirms their regular nature. In the process of smoothing the curves, all the observed steps would be inevitably lost due to their small size, which would lead to an erroneous conclusion about the full compliance of the data with the Gompertz law.

Fig. 6. Rank mortality curves of the first subgroup of 62 males (top curve) and the second subgroup of 53 males (bottom curve) obtained by dividing the rank of 115 normal males arranged according to the dates of their half-lives.

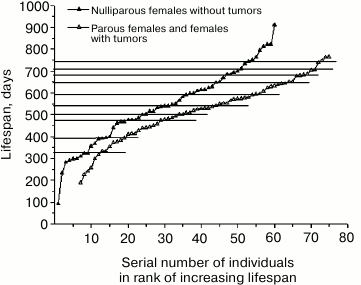
The situation with the rank mortality curve of normal females presented in Fig. 5 seems to be different. Earlier [11, 12] it was suggested that flattening of the steps on the rank mortality curve of normal females was caused by the shifts in development resulting from irregularity of their reproduction. At the present time, sufficient data on the lifespan of different females (parous and nulliparous ones) have been accumulated to verify this hypothesis. Indeed, the deletion of data on the lifespan of parous females from the rank mortality curve led to a partial manifestation of characteristic steps. A more pronounced result was obtained when, along with the previously mentioned data, data on the lifespan of females with tumors were also deleted from the curve.

Figure 7 shows the rank mortality curve of nulliparous females without tumors and a similar curve compiled from data on lifespan of parous females or those with tumors. While steps characteristic for the curves of mutant mice and normal males can be clearly seen on the first curve (age intervals corresponding to these steps are separated by points 325-390-475-500-540-590-680-710-740 days), the second curve is rather smooth without any significant deviations except for the intervals 650-680 days and 710-740 days at the end of the curve, which coincide with corresponding intervals on the curve of nulliparous females and those without tumors. This can be explained by the fact that in the case of a smooth curve, lifespan is determined not by a strict program of organismal development, but by uncontrollable external causes. On the other hand, the presence of steps on the curve of nulliparous females, which makes this curve qualitatively different from the smooth curve of parous females and females with tumors, indicates that these steps result from an internal development program.

Fig. 7. Rank mortality curves of 60 normal nulliparous females without tumors (top curve) and 69 normal parous females and females with tumors (bottom curve).

High level of expression of steps on the rank mortality curve of normal females observed in case of simultaneous deletion of data on the lifespan of parous females and females with tumors indicates that these conditions cause comparable changes in animals. In this regard, one cannot but recall the recommendations of oncologists to treat breast or ovarian cancer by pregnancy. It is also known that veterinarians use ovariectomy to prevent the development of tumors in nulliparous females of domestic animals. In our case, tumors were more frequent in normal nulliparous females than in parous ones. It should also be noted that tumors hardly ever developed in normal and mutant males and relatively rarely in mutant females.

Proximity of characteristics of age intervals for the steps on rank mortality curves of mutant mice and normal males older than 400 days suggests the mutation causing growth retardation has no significant effect on the further development of mice.

Reproducibility of steps on the rank mortality curves suggests that the observed deviations of experimental curves from theoretical ones based on the parameters of the Gompertz–Makeham equation are not random, and they point to the inadequacy of the Gompertz–Makeham model.

Since the steps on the rank mortality curves of normal mice are far less pronounced than in case of mutant mice, the latter can serve as a convenient model to study the nature of the stages of sustainable development and stages of increased death risk in normal mice.

Development of many physiological processes in time is programmed in a species-specific manner. Adjustments of the organism in the times of transition to puberty, pregnancy, and menopause are examples of this phenomenon. Such stages of development as menstrual cycle in women, molting in representatives of different taxonomic groups (larvae of insects, reptiles, some mammals, etc.), and change of teeth in some animals are regularly repeated and strictly determined in time. In this regard, death can be seen as a final stage in the physiological development of an organism.

However, the time of individual deaths in a population is not absolutely determined. Random (stochastic) external factors, such as different pathogens, malnutrition, or unfavorable environmental conditions can affect the time of deaths of individuals. Poor predictability of individual lifespan and the practice of statistical description of individual lifespans in a population by smooth analytical functions, which change monotonically in time, is consistent with the models of stochastic mechanisms of aging [5, 8].

On the other hand, there are statistical data on the narrowed age limits of morbidity and mortality in pairs of identical twins compared to fraternal twins, examples of death dates coinciding with the end of the processes of fertilization or fruiting (spawning salmon, one-day butterflies, annual plants, etc.) and the above-described consecutive change of stages of sustainable development by the stages of increase death risk in mice. All these data suggest death to be caused by the completion of an internal program of organismal development.

All the data in favor of internal programming of lifespan and those in favor of it being affected by random external factors can be reconciled within the hypothesis according to which it is not the death itself, but its probability caused by periodic changes of organismal sensitivity to unfavorable environmental effects, that is programmed. At the beginning of this article we discussed the fact of maximal sensitivity of normal mice to ionizing radiation [13] coinciding in time with the first step of deaths of mutant mice on the curves of rank distribution. This observation directly supports our hypothesis. The fact that only a small portion of a population usually dies as the result of epidemics caused by external factors is also consistent with this hypothesis. The very division into the diseases characteristic for children, mature, and old age and selection of conditions that provoke them indicate the presence of critical and sustainable stages in organismal development in relation to specific environmental effects.

The hypothesis of programmed death probability suggests that, using the information about the threat of a critical development stage coinciding with adverse environmental conditions, it is possible to avoid premature death by creating conditions that prevent damaging environmental effects, or by increasing individual sensitivity threshold to external impacts by medical treatments. Such overcoming of the barrier of a critical development stage opens the transition to the next stage of sustainable development.

Thus, proving the presence of critical development stages in human ontogenesis and developing the methods of their diagnosis and amelioration would open prospect for extending lifespan to the species maximum (about 105 years) in currently living individuals. Earlier we discussed similarities in the positions of clearly pronounced fluctuations on the curves of the logarithm of human mortality intensity at ages before 25 years (Fig. S2 in Supplement) and after 90 years (Fig. S3 in Supplement) observed by different researchers [7, 17, 18]. This observation suggests that in the interval between those ages less pronounced fluctuations may occur that occupy defined positions on the time axis. Attempts have been made to find evidence of the existence of critical development stages in populations of intermediate ages on the basis of calculation of the available statistical data [20]. Observed mass mortality of 60-year-old men from heart attacks can be interpreted within this hypothesis as the result of their reaching a critical stage of physiological adjustment that they cannot overcome in the given socioeconomic conditions.

The author expresses his gratitude to L. A. Denisova, Director of the Vivarium of the Institute of Biochemistry of the Russian Academy of Sciences for comprehensive assistance in the technical part of the experiment.

This work was supported by the Russian Foundation for Basic Research grant No. 11-04-01615a.

REFERENCES

1.Bernar, K. (1937) Lectures on Experimental Pathology [in Russian], Gosudarstvennoe Izdatelstvo Biologicheskoi i Meditsinskoli Literatury, Moscow-Leningrad.
2.Pavlov, I. P. (1951) Complete Set of Works [in Russian], 2nd Edn., Vol. 1, Izdatelstvo Akademii Nauk SSSR, Moscow-Leningrad.
3.Big Medical Encyclopedia (1985) Vol. 24, Thanatology [in Russian], Sovetskaya Entsiklopediya, Moscow.
4.Skulachev, V. P., and Longo, V. D. (2005) Ann. N. Y. Acad. Sci., 1054, 145-164.
5.Khalyavkin, A. V. (1998) Uspekhi Gerontol., 2, 43-48.
6.Gompertz, B. (1825) Philos. Trans. Roy. Soc. London A, 115, 513-583.
7.Lamb, M. (1980) Biology of Aging [Russian translation], Mir, Moscow.
8.Gavrilov, L. A., and Gavrilova, N. S. (1991) Biology of Life Expectancy [in Russian], Nauka, Moscow.
9.Makeham, W. M. (1860) J. Inst. Actuaries, 8, 301-310.
10.Moskalev, A. A. (2008) Aging and Genes [in Russian], Nauka, St. Petersburg.
11.Malygin, A. G. (2012) Doklady MOIP Sektsiya Gerontol., 50, 56-65.
12.Malygin, A. G. (2013) Ontogenez, 44, 57-65.
13.Grosfill, M. L., Lindop, P. J., and Rotblat, J. (1959) Nature, 183, 1729-1730.
14.Frolkis, V. V. (1969) Nature of Aging [in Russian], Nauka, Moscow.
15.Schmalhausen, I. I. (1984) Growth and Differentiation, Vol. 1 [in Russian], Naukova Dumka, Kiev.
16.Anisimov, V. N. (2008) Molecular and Physiological Mechanisms of Aging, Vol. 2 [in Russian], Nauka, St. Petersburg.
17.Depoid, F. (1973) Population, 28, 755-792.
18.Vaupel, J. W., Carey, J. R., Christeansen, K., Johnson, T. E., Yashin, A. I., Holm, N. V., Iachint, I. A., Kannisto, V., Khazaeli, A. A., Liedo, P., Longo, V. D., Zeng, Y., Manton, K. G., and Curtsinger, J. W. (1998) Science, 280, 855-860.
19.Mathematical Encyclopedia (1984) Vol. 4, Averaging [in Russian], Sovetskaya Entsiklopediya, Moscow.
20.Frank, S. A. (2004) BMC Biology, 2, 16; doi:10.1186/1741-7007-2-16 (http://www.biomedcentral.com/1741-7007/2/16).

SUPPLEMENT

Supplementary FIGURES & TABLE (PDF)