REVIEW: Mechanism of Primary and Secondary Ion-Radical Pair Formation in Photosystem I Complexes
G. E. Milanovsky1, V. V. Ptushenko1, D. A. Cherepanov2, and A. Yu. Semenov1*
1Belozersky Institute of Physico-Chemical Biology, Lomonosov Moscow State University, 119992 Moscow, Russia; fax: +7 (495) 939-3181; E-mail: semenov@genebee.msu.ru2Frumkin Institute of Physical Chemistry and Electrochemistry, Russian Academy of Sciences, 119071 Moscow, Russia; fax: +7 (495) 952-5308
* To whom correspondence should be addressed.
Received November 24, 2013
The mechanisms of the ultrafast charge separation in reaction centers of photosystem I (PS I) complexes are discussed. A kinetic model of the primary reactions in PS I complexes is presented. The model takes into account previously calculated values of redox potentials of cofactors, reorganization energies of the primary P700+A0- and secondary P700+A1- ion-radical pairs formation, and the possibility of electron transfer via both symmetric branches A and B of redox-cofactors. The model assumes that the primary electron acceptor A0 in PS I is represented by a dimer of chlorophyll molecules Chl2A/Chl3A and Chl2B/Chl3B in branches A and B of the cofactors. The characteristic times of formation of P700+A0- and P700+A1- calculated on the basis of the model are close to the experimental values obtained by pump–probe femtosecond absorption spectroscopy. It is demonstrated that a small difference in the values of redox potentials between the primary electron acceptors A0A and A0B in branches A and B leads to asymmetry of the electron transfer in a ratio of 70 : 30 in favor of branch A. The secondary charge separation is thermodynamically irreversible in the submicrosecond range and is accompanied by additional increase in asymmetry between the branches of cofactors of PS I.
KEY WORDS: photosystem I, reaction center, electron transfer, primary reactions, kinetic modelingDOI: 10.1134/S0006297914030079
Abbreviations: A0A and A0B, chlorophyll primary electron acceptor in branches A and B; A1A and A1B, phylloquinone molecules (secondary electron acceptors in branches A and B); Chl, chlorophyll; Chl1A/Chl1B, Chl2A/Chl2B, and Chl3A/Chl3B, first, second, and third pairs of chlorophyll molecules in symmetric branches of redox cofactors A and B of PS I; P700, chlorophyll dimer (the primary electron donor); PS I, photosystem I; RC, reaction center.
Photosynthetic reaction centers (RC) are usually grouped into two types
depending on the nature of the terminal acceptor. Type II RCs include
those of purple bacteria and photosystem II and contain loosely bound
quinone as terminal acceptor. Type I RCs include homodimeric RCs of
green photosynthetic bacteria Chlorobium and
Chloracidobacterium and heliobacteria Heliobacteriaceae, and
heterodimeric RC of photosystem I (PS I) from plants and cyanobacteria
that have protein-bound iron–sulfur cluster as the acceptor [1]. PS I of cyanobacteria contains 12 protein
subunits, 96 chlorophyll molecules (Chl), 22 carotenoids, three
[4Fe-4S] clusters, two phylloquinones, and four lipid molecules. Two
transmembrane subunits PsaA and PsaB form a C2-symmetric
heterodimeric core complex containing most of the cofactors [2] (Fig. 1).
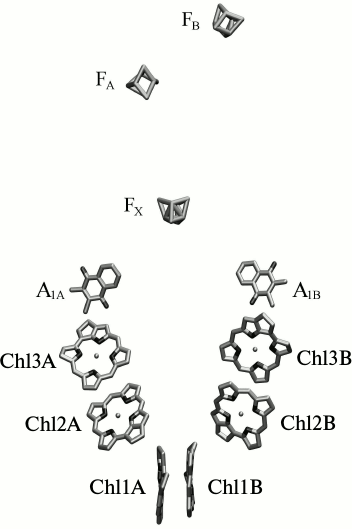
Fig. 1. Localization of the redox cofactors of electron transfer in reaction center of PS I. Chl1A(B), Chl2A(B), Chl3A(B) – first, second, and third pairs of chlorophyll molecules in the symmetric branches of redox cofactors A and B; A1A, A1B – phylloquinone molecules in branches A and B; FX, FA, and FB – [4Fe-4S] clusters.
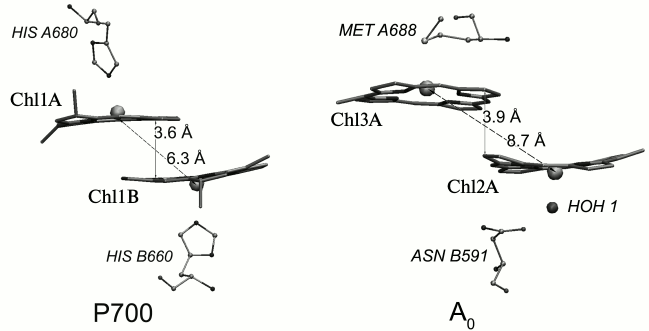
Out of 96 Chl molecules, six are electron transfer cofactors and are localized near the contact surfaces of the PsaA and PsaB subunits. The chlorophyll dimer P700 consists of two Chl a molecules (Chl1A/Chl1B), the porphyrin planes of which are parallel to each other (with distance of 3.6 Å) and perpendicular to the plane of the membrane. The spatial localization of the other two molecules of Chl a (Chl2A/Chl2B) roughly corresponds to the localization of two molecules of monomeric bacteriochlorophyll in the RC of purple bacteria, and two more molecules of Chl a (Chl3A and Chl3B) are arranged similarly to two molecules of bacteriopheophytin in RC of purple bacteria [3, 4]. The planes of the porphyrin rings of Chl2A (Chl2B) and Chl3A (Chl3B) molecules are parallel (with distance of 3.9 Å), but they are slightly more shifted relative to each other than Chl1A and Chl1B (Fig. 2). PS I also includes two molecules of phylloquinone (A1A and A1B). The pairs of Chl and phylloquinone molecules are arranged in two symmetric branches A and B and bound with PsaA and PsaB subunits, respectively. Branch A includes molecules Chl1A, Chl2A, Chl3A, and phylloquinone A1A, while branch B includes Chl1B, Chl2B, Chl3B, and phylloquinone A1B. The two cofactor branches of the electron transfer chain merge on inter-polypeptide iron–sulfur cluster FX. Terminal electron acceptors – [4Fe-4S] clusters FA and FB – are localized on the stromal subunit PsaC. The electron transfer chain PS I consists of P700, A0 (one or both pairs of Chl molecules designated as Chl2A/Chl3A and Chl2B/Chl3B), A1 (one or both phylloquinone molecules A1A/A1B), and iron–sulfur clusters FX, FA, and FB. It is now known that the electron transfer in PS I occurs through both branches of the redox cofactors from P700 to FX, but the degree of asymmetry of this transfer and the factors that cause it are not clear [5, 6]. In addition, to date the kinetics of the primary charge separation and even the nature of the primary electron donor and acceptor in PS I remain controversial [6, 7]. This review discusses and analyzes the energetic and kinetic data that clarify the mechanism of the primary stages of electron transfer in PS I.
Fig. 2. Relative arrangement in the dimers of chlorophyll molecules constituting the primary donor P700 (Chl1A and Chl1B) and the primary electron acceptor A0A (Chl2A/Chl3A) in PS I in branch A of redox cofactors. The axial ligands to the central Mg atom of chlorophyll molecules and the distance between the plane of the porphyrin rings and Mg atoms are noted.
EXPERIMENTAL STUDIES OF THE PRIMARY STAGES OF ELECTRON TRANSFER
IN PS I
We have recently shown that after the preferential excitation of P700 the formation of the primary radical pair P700+A0- occurs within 100 fs, and the subsequent electron transfer forming P700+A1- has a characteristic time of ~25 ps [7]. Subsequent electron transfer reactions from A1A- and A1B- to FX occur with characteristic times of ~200 and ~20 ns, respectively [5, 6, 8, 9]. Then sequential electron transfer occurs from FX to the terminal iron–sulfur clusters FA and FB and further still to the soluble proteins ferredoxin or flavodoxin. Photooxidized P700+ is reduced by plastocyanin or cytochrome c6, returning all cofactors of PS I back to their original state, where the primary electron donor P700 is reduced and all subsequent acceptors are oxidized. In the absence of exogenous electron donors and acceptors, the charge-separated state P700+[FA/FB]- recombines to the ground state with a characteristic time of ~50 ms [10, 11].
Chl2A/Chl2B and Chl3A/Chl3B molecules, constituting the primary acceptor A0, are characterized by unusual axial ligands, namely, water in the case of Chl2A/Chl2B and methionine residues in the case of Chl3A/Chl3B. The methionine residues (Met688PsaA and Met668PsaB) are conserved in all known species of plants and cyanobacteria. These methionine residues have been replaced in cyanobacteria mutants by leucine, histidine, and asparagine residues [12-14]. Ultrafast optical measurements demonstrated that the electron transfer kinetics from A0- to A1 is slowed in PS I from the mutants in branch A (M688LPsaA, M688NPsaA, and M688HPsaA), while the kinetics of the mutants in branch B (M668LPsaB, M668NPsaB, and M668HPsaB) do not differ from the kinetics of PS I observed in the wild-type cyanobacteria [13, 14]. These data indicate the asymmetric contribution of cofactor branches A and B in the formation of secondary ion-radical pair P700+A1-. Time-resolved study of the EPR spectra of PS I mutants M688NPsaA and M668NPsaB at the frequency of 95 GHz (W-band) at 100 K demonstrated that the kinetics of charge recombination were similar in PS I from the wild-type and the branch B mutant and was significantly different in PS I from the branch A mutant [15]. Analysis of the electron spin echo envelope modulation (ESEEM) showed that the distances between the centers of ion-radical pair P700+A1- in PS I from the wild-type and from the branch B mutant correspond to electron transfer only through the A branch.
CALCULATIONS OF ENERGETIC CHARACTERISTICS OF PRIMARY CHARGE
SEPARATION IN PS I
Estimation of the energetic characteristics of the electron transfer in PS I is crucial for theoretical description of the primary charge separation and interpretation of the experimental data described in the previous section. In this section we will briefly describe the results of our calculations of redox potentials of PS I cofactors, obtained by estimation of the electrostatic interactions between cofactors and protein and with each other, based on its atomic structure ([2], PDB code 1JB0).
Functioning of the system of molecules with the same chemical nature (Chl molecules) in the sequence of redox reactions as both donors and acceptors of electron is possible due to the modification of their redox properties through the interaction with the protein environment. The greatest influence on the redox potentials of P700 and A0 is caused by the interaction between Chl molecules of RC with their axial ligands and by the electric dipole moments of the peptide groups.
The ligands of Chl1A and Chl1B molecules are histidines, the ligands of Chl2A and Chl2B are water molecules, and the ligands of Chl3A and Chl3B are methionines (Fig. 2). The imidazole ring of histidine has a significantly greater electric dipole moment than a water molecule or a methionine residue. The Nε-atom of the imidazole ring of histidine carries a negative charge of ~0.56-0.57 elementary charge [16, 17]. As the histidine ring, which is the ligand of Chl1A (Chl1B), is directed to the central Mg atom with this atom, it creates a significant negative electrical potential in the tetrapyrrole rings of P700 (–0.23 V according to our calculations within the macroscopic model described in [18]), stabilizing the oxidized state of the molecule. For other ligands – water molecules and methionine – this electrostatic effect is ~(–0.1 V) [18]. Influence of the local electric field distribution in the protein on the redox potentials of cofactors – Chl molecules – leads to the fact that electron transfer from P700* to the primary electron acceptor, which consists of Chl3A (Chl3B) or Chl2A/Chl3A dimer (Chl2B/Chl3B dimer), is energetically favorable.
In addition to these effects, which can be described in terms of classical electrostatics, an important role in determining the redox properties of P700 and A0, which is necessary for the primary charge separation, is played by the electronic conjugation arising from the interaction of π-orbital systems of parallel porphyrin rings. As the result of such interaction of π-orbital systems, the charge is delocalized over both porphyrin rings, and two chlorophyll molecules can function as a single redox center, A0. In this case the negative charge, appearing on Chl2 and Chl3 molecules as the result of photo-induced charge separation in PS I, is stabilized as compared with the case of non-interacting Chl2 and Chl3 molecules. This effect is manifested in some increase in the redox potential of the A0/A0- couple. According to our calculations using the methods of quantum chemistry, this increase is ~0.045 V; a similar coupling effect exists for P700, lowering the value of Em(P700/P700+), as compared with the redox potentials of monomeric chlorophyll molecules forming the P700, by 0.095 V [18].
We calculated the redox potential (Em) of the primary electron donor (P700/P700+) by the semi-continuum approach (taking into account the heterogeneity of the dielectric constant of PS I) in combination with quantum chemistry methods (taking into account the effect of electron pairing in the P700 dimer); this value was found to be +0.45 V [18]. When PS I is excited by light with a wavelength of 700 nm (quantum energy of 1.77 eV), electronic excitation is localized on the dimer P700, turning it into a strong reducer P700* with Em value of P700*/P700+ pair equal to –1.32 V, which is 50-90 mV less than Em of the primary acceptor A0 (Em of the A0A/A0A- pair is –1.23 V; Em of the A0B/A0B- pair is –1.27 V [18]).
An alternative model of the primary stages of charge separation in PS I was recently proposed [19], in which the role of the primary electron donor is played by monomeric Chl2A (Chl2B), and the role of the primary acceptor is assumed by Chl3A monomer (Chl3B). Analysis of the electrostatic interactions between the molecules of chlorophyll Chl2A (Chl2B) and Chl3A (Chl3B) with their protein environment apparently evidences against this hypothesis. Calculation of the redox potential of the Chl2A/Chl2A+ and Chl2B/Chl2B+ pairs gives the value of +0.82 V, and the potential of Chl3B/Chl3B- and Chl3A/Chl3A- pairs, which correspond to A0 in this model, is ~(–1.01 V) [18]. As a result, the redox potential of the hypothetical acceptor (redox couple Chl3/Chl3-) becomes about 60 mV lower than the potential of the hypothetical donor (redox couple Chl2*/Chl2+). Thus in this model the primary charge separation between Chl2A (Chl2B) and Chl3A (Chl3B) is thermodynamically unfavorable, and the functioning of Chl2A (Chl2B) as the primary electron donor seems unlikely.
MODELING THE KINETICS OF FORMATION OF THE PRIMARY AND SECONDARY
ION-RADICAL PAIRS
Electron transfer in biological systems can be described in terms of Marcus theory [20], which links the transfer rate constant to the free energy of the reaction, the reorganization energy of the system, and the electronic conjugation between the donor and acceptor. Several empirical approximations were proposed to describe the dependence of the electronic coupling on the distance between donor and acceptor in proteins [21, 22].
Previously Santabarbara et al. [23] proposed a kinetic model of PS I, constructed on the basis of Marcus equation in Moser–Dutton approximation [21], that takes into consideration the possibility of an independent electron transfer through either branch of cofactors (A or B). The distances between the redox cofactors in the model were taken from the crystallographic structure of PS I, and the values of the redox potentials of cofactors and estimates of the reorganization energies of the corresponding reactions were obtained from indirect data published previously [19, 24]. The kinetics of formation of the primary and secondary ion-radical pairs in this model were distinct for the two branches of cofactors with characteristic times τ of 8.9 and 6.5 ps for the primary charge separation and 35.5 and 25 ps for the secondary separation along branches A and B, respectively. These kinetics, calculated within the framework of this model, contradict the experimental data with femtosecond resolution on the primary ion-radical pair formation [7].
Recently in our laboratory molecular dynamics studies of PS I were performed [25], which made it possible to estimate the reorganization energy λ of the primary and secondary charge separation reactions in both branches of cofactors. Within the framework of the molecular dynamics model, we considered the primary electron acceptor to consist either of the third chlorophyll Chl3A/Chl3B [25], or the dimer of second and third chlorophylls Chl2A/Chl3A and Chl2B/Chl3B with uniform charge distribution between two chlorophyll molecules (our unpublished data). According to the latter model, the value of the outer-sphere reorganization energy λout of the primary charge separation on characteristic time of ~100 fs is ~70 mV, and λout of the secondary charge separation over the time of 100 ps is 550 mV in both branches of cofactors. Inner-sphere reorganization energy value λin was taken as 100 mV [26, 27].
Due to significant discrepancy in estimates based on the model of Santabarbara et al. with experimental data, we attempted to clarify the characteristics of the primary and secondary charge separation reactions in PS I. To describe the kinetics of formation of the primary and secondary ion-radical pairs in both branches of the redox cofactors, we used a system of differential equations described in [23], except for the step of electron excitation transfer from the antenna to P700, which was not simulated. To estimate the values of the PS I cofactor redox potentials and the free energy of charge separation reactions ΔG, we used the data obtained by the semi-continuum approach, which takes into account the heterogeneous distribution of the dielectric constant in PS I and the influence of preexisting protein electrostatic field [18]. The values of reorganization energy λ were taken from the results of molecular dynamics simulation described above [25], as well as from our preliminary calculations. Rates of forward and reverse electron transfer were calculated by the semi-empirical Moser–Dutton equation [21] using these estimates of λ, ΔG, and the distances between cofactors measured during the molecular modeling. The results are presented in the table.
Calculation of the characteristic times of formation of the primary
(P700+A0-) and secondary
(P700+A1-) ion-radical pairs and the
relative contributions of cofactor branches A and B in
electron transfer

Note: The table shows the reorganization energy (λ1,
λ2), free energy change (ΔG1,
ΔG2), as well as the characteristic times of
the forward electron transfer (τ1, τ2)
and the relative contributions of redox cofactors branches A and
B (A1, A2) to the primary and secondary
electron transfer.
a, b Data obtained from references [23]
and [16], respectively.
According to this model, the characteristic time τ1 of the primary charge separation (formation of P700+A0- pair) was 0.1-0.3 ps, and the characteristic time of the secondary charge separation (P700+A1- pair) τ2 was 16-20 ps, which is in good agreement with the experimental results obtained with the direct excitation of Chl molecules of RC with femtosecond time resolution [7]. It is notable that the slight difference in redox potentials between the primary electron acceptors A0A and A0B in branches A and B led to the emergence of the asymmetry in the electron transfer in the ratio of 70 : 30 in favor of branch A. The model also predicts a very fast (<7 ps) equilibration between states P700+A0A- and P700+A0B-, which is faster than the characteristic time τ2 of the secondary ion-radical pair P700+A1- formation. The secondary charge separation process is kinetically irreversible on the submicrosecond time scale since recombination of charges in the P700+A1- pair occurs on a time scale that is several orders of magnitude greater than the characteristic time of the forward transfer from A1 to FX and is accompanied by increased asymmetry between the cofactor branches of PS I in favor of branch A.
It should be noted that the use of the Marcus equation derived in non-adiabatic approximation for the description of ultrafast reactions of the primary charge separation with a characteristic time of 100 fs is not indisputable. It is very likely that the kinetics of the primary ion-radical pair formation is affected by vibrational modes of the protein, which are ignored by the Marcus model. Such oscillations were observed experimentally by us earlier [28]. In addition, the empirical Moser–Dutton equation was obtained for transfer reactions at the distance of ≥10 Å, whereas the distance between the primary electron donor P700 and the second pair of chlorophyll molecules Chl2A/Chl2B does not exceed 4 Å.
This paper is dedicated to the memory of the remarkable Russian scientist – founder of national photobiochemistry and pioneer in the study of light-dependent electron transfer in photosynthesis – Alexander Abramovich Krasnovsky. One of the authors (A.Yu.S.) had the good fortune and honor to discuss the mechanism of photosynthetic electron transfer with Prof. A. A. Krasnovsky many times. On the initiative of A. A. Krasnovsky, collaboration was started in 1986 with the laboratory of his disciple, V. A. Shuvalov, on the kinetics of electron transfer in the reaction centers of the photosynthetic bacterium Rhodopseudomonas (Blastochloris) viridis, for which the X-ray crystal structure with atomic resolution was first obtained [3]. At the present time, this cooperation continues in the study of the primary reactions of charge transfer in PS I and PS II complexes [7, 14, 29].
This study was supported by the Russian Foundation for Basic Research (grants 11-04-91330, 12-04-00821, and 13-04-40299-H) and CRDF grant RUB1-7029-MO-11.
REFERENCES
1.Sadekar, S., Raymond, J., and Blankenship, R. E.
(2006) Mol. Biol. Evol., 23, 2001-2007.
2.Jordan, P., Fromme, P., Witt, H. T., Klukas, O.,
Saenger, W., and Krauß, N. (2001) Nature, 411,
909-917.
3.Deisenhofer, J., Epp, O., Miki, K., Huber, R., and
Michel, H. (1985) Nature, 318, 618-624.
4.Komiya, H., Yeates, T. O., Rees, D. C., Allen, J.
P., and Feher, G. (1988) Proc. Natl. Acad. Sci. USA, 85,
9012-9016.
5.Guergova-Kuras, M., Boudreaux, B., Joliot, A.,
Joliot, P., and Redding, K. (2001) Proc. Natl. Acad. Sci. USA,
98, 4437-4442.
6.Srinivasan, N., and Golbeck, J. H. (2009)
Biochim. Biophys. Acta Bioenerg., 1787, 1057-1088.
7.Shelaev, I. V., Gostev, F. E., Mamedov, M. D.,
Sarkisov, O. M., Nadtochenko, V. A., Shuvalov, V. A., and Semenov, A.
Y. (2010) Biochim. Biophys. Acta Bioenerg., 1797,
1410-1420.
8.Brettel, K. (1988) FEBS Lett., 239,
93-98.
9.Setif, P., and Bottin, H. (1989)
Biochemistry, 28, 2689-2697.
10.Sauer, K., Mathis, P., Acker, S., and Van Best,
J. A. (1978) Biochim. Biophys. Acta, 503, 120-134.
11.Vassiliev, I. R., Jung, Y. S., Mamedov, M. D.,
Semenov, A., and Golbeck, J. H. (1997) Biophys. J., 72,
301-315.
12.Cohen, R. O., Shen, G., Golbeck, J. H., Xu, W.,
Chitnis, P. R., Valieva, A. I., van der Est, A., Pushkar, Y., and
Stehlik, D. (2004) Biochemistry, 43, 4741-4754.
13.Dashdorj, N., Xu, W., Cohen, R. O., Golbeck, J.
H., and Savikhin, S. (2005) Biophys. J.,
88, 1238-1249.
14.Semenov, A. Y., Mamedov, M. D., Golbeck, J. H.,
Shuvalov, V. A., and Nadtochenko, V. A. (2013) in Abst. Int. Conf.
“Photosynthesis Research for Sustainability” (Feyziyev,
Y. M., Huseinova, I. M., and Allakhverdiev, S. I., eds.) Nurlar, Baku,
p. 79.
15.Savitsky, A., Gopta, O., Mamedov, M., Golbeck, J.
H., Tikhonov, A., Moebius, K., and Semenov, A. (2010) Appl. Magnet.
Resonance, 37, 85-102.
16.Cornell, W. D., Cieplak, P., Bayly, C. I., Gould,
I. R., Merz, K. M., Ferguson, D. M., Spellmeyer, D. C., Fox, T.,
Caldwell, J. W., and Kollman, P. A. (1995) J. Am. Chem. Soc.,
117, 5179-5197.
17.Sitkoff, D., Sharp, K. A., and Honig, B. (1994)
J. Phys. Chem., 98, 1978-1988.
18.Ptushenko, V. V., Cherepanov, D. A., Krishtalik,
L. I., and Semenov, A. Y. (2008) Photosynth. Res., 97,
55-74.
19.Muller, M. G., Niklas, J., Lubitz, W., and
Holzwarth, A. R. (2003) Biophys. J., 85, 3899-3922.
20.Marcus, R. A., and Sutin, N. (1985) Biochim.
Biophys. Acta, 811, 265-322.
21.Moser, C. C., and Dutton, P. L. (1992)
Biochim. Biophys. Acta, 1101, 171-176.
22.Onuchic, J. N., Beratan, D. N., Winkler, J. R.,
and Gray, H. B. (1992) Annu. Rev. Biophys. Biomol. Struct.,
21, 349-377.
23.Santabarbara, S., Heathcote, P., and Evans, M. C.
W. (2005) Biochim. Biophys. Acta, 1708, 283-310.
24.Ishikita, H., and Knapp, E.-W. (2003) J. Biol.
Chem., 26, 52002-52011.
25.Milanovsky, G. E., Ptushenko, V. V., Golbeck, G.
H., Semenov, A. Yu., and Cherepanov, D. A. (2014) Biochim. Biophys.
Acta, in press.
26.Sigfridsson, E., Olsson, M. H. M., and Ryde, U.
(2001) J. Phys. Chem. B, 105, 5546-5552.
27.Amashukeli, X., Gruhn, N. E., Lichtenberger, D.
L., Winkler, J. R., and Gray, H. B. (2004) J. Am. Chem. Soc.,
126, 15566-15571.
28.Sarkisov, O. M., Gostev, F. E., Shelaev, I. V.,
Novoderezhkin, V. I., Gopta, O. A., Mamedov, M. D., Semenov, A. Y., and
Nadtochenko, V. A. (2006) Phys. Chem. Chem. Phys., 8,
5671-5678.
29.Shelaev, I. V., Gostev, F. E., Vishnev, M. I.,
Shkuropatov, A. Ya., Ptushenko, V. V., Mamedov, M. D., Sarkisov, O. M.,
Nadtochenko, V. A., Semenov, A. Yu., and Shuvalov, V. A. (2011) J.
Photochem. Photobiol. B: Biol., 104, 44-50.