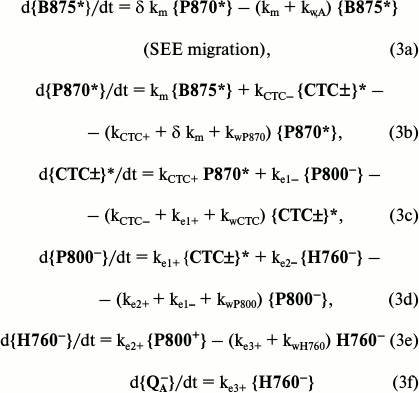REVIEW: Efficiency of Photochemical Stages of Photosynthesis in Purple Bacteria (A Critical Survey)
A. Yu. Borisov
Lomonosov Moscow State University, Belozersky Institute of Physico-Chemical Biology, 119992 Moscow, Russia; fax: (495) 939-3181; E-mail: ayb280630@yandex.ru
Received October 28, 2013; Revision received December 1, 2013
Based on currently available data, the energy transfer efficiency in the successive photophysical and photochemical stages has been analyzed for purple bacteria. This analysis covers the stages starting from migration of the light-induced electronic excitations from the bulk antenna pigments to the reaction centers up to irreversible stage of the electron transport along the transmembrane chain of cofactors-carriers. Some natural factors are revealed that significantly increase the rates of efficient processes in these stages. The influence on their efficiency by the “bottleneck” in the energy migration chain is established. The overall quantum yield of photosynthesis in these stages is determined.
KEY WORDS: photosynthesis, purple bacteria, efficiency of energy migration and trappingDOI: 10.1134/S0006297914030080
Abbreviations: BChl, bacteriochlorophyll; RC, reaction center; SEE, singlet electronic excitation; * indicates the SEE presence in a molecule or in a group of molecules.
The world of photosynthesis is a unique symbiosis of processes
responsible for the annual reservation on Earth of about
3·1024 J of energy in the biomass of plants, algae,
and photobacteria [1, 2].
Historically, Krasnovsky’s reaction was the first model of
photosynthesis: Krasnovsky realized in the liquid phase the reversible
photoreduction of chlorophyll a molecules with ascorbic acid
that is accompanied by an increase in the free chemical energy of the
system [3-5]. It should be
noted that Krasnovsky was inspired to study photochemical reactions of
chlorophyll by Academician A. N. Terenin, who in 1943 discovered the
relatively long-lived triplet state in molecules of dyes and developed
ideas about their effective involvement in photochemical reactions [6]. In fact, the first works of Krasnovsky and his
colleagues revealed that it was the triplet state of chlorophyll that
was responsible for its photoreduction in solutions (works [3-5] and references therein).
Later, reactions of the chlorophyll triplet state were studied in
detail using a flash-photolysis approach ([7] and
references). The works of Krasnovsky and Terenin [3-6] had great resonance in
science, and many photochemists replenished the series of researchers
in photosynthesis. However, over time some works appeared whose results
did not fit the triplet mechanism of photosynthesis. The study of
Dmitrievsky et al. [8] stimulated by A. N. Terenin
showed that the lifetime of chlorophyll a in algae and
chloroplasts is approximately fourfold lower than the chlorophyll
a lifetime in solutions. Similar results were obtained by Brody
and Rabinovich for the algae Chlorella [9].
However, for a long time a burning question existed for researchers:
why are no triplets found in chlorophylls in preparations of
photosynthesizing organisms? After numerous unsuccessful attempts in
laboratories of different countries, triplets were recorded in
chlorophyll of chloroplasts, but the yield was extremely low [10]. This effect was, in particular, mainly
determined by an exclusively high rate of energy utilization within the
reaction centers of photosynthesis, as first established in the works
of Godik and the author of this article [11-13]. These works have shown that in four purple
bacteria the fluorescence lifetime of bacteriochlorophyll (BChl) is in
the range of dozens of picoseconds. This lifetime increased by nearly
an order of magnitude during photooxidation (outcome from the active
state) of the reaction centers (RC). Later the picosecond range of the
singlet BChl lifetimes in vivo was confirmed in studies of
Paschenko et al. [14], Campillo et al. [15], and in some subsequent works using picosecond
laser approaches. Based on these ultrashort times, the principle of
instantaneous action of photosynthesis was formulated [16, 17]. This principle means
that the energy migration and conversion during photosynthesis occur
with a significantly higher rate than the losses, and this provides for
a high quantum yield of photosynthesis as a whole.
These works and also some following ones resulted in the adoption of the singlet model of the primary processes of photosynthesis. The main advantage of this model is that it admits migrations of singlet electronic excitations (SEE) among molecules over significant distances, dozens of angstroms (!). This is very important because RCs in representatives of the world of photosynthesis have to efficiently harvest SEE from tens to hundreds of “antenna” chlorophyll molecules.
Systems of antenna chlorophylls of photosynthesizing organisms are heterogeneous; they contain series of spectral forms that produce energy “funnels” for the preferential “flow” of SEE to the long-wavelength RCs. The number of individual forms of chlorophylls in plants and algae reaches 12-15. It has now been shown that in the known photosynthesizing organisms the SEE migration from the mass of antenna chlorophylls and the rate of their trapping by RCs mainly determine the quantum yield of photosynthesis. This is the problem considered in this work.
ANALYSIS OF FACTORS STIMULATING ENERGY MIGRATION FROM THE
MOLECULAR ANTENNA TO THE REACTION CENTERS IN PURPLE BACTERIA
The organization of the primary stages of photosynthesis (light absorption, energy migration through the antenna molecules to the RCs transforming the SEE energy, separation in the RCs of oppositely signed charges and their transfer onto the opposite sides of membranes) indicates that they are a typical photoelectric system. In this field of biological solar energetics researchers are especially interested in the general principles and mechanisms of transfer and conversion of absorbed light energy by the chlorophyll–protein apparatus of photosynthesizing organisms. For studies in this field, the easiest representatives of the photosynthesis world are, namely, the purple bacteria, which possess a number of important advantages.
1) As differentiated from plants possessing mixed structures, spectra, and functions of two photosystems, purple bacteria have only one photosystem.
2) Purple bacteria have 30-32 long-wavelength RC-bound BChl molecules per RC that convert electronic excitations [18, 19]. This is several times less than in plants, and this significantly facilitates studies on functioning reaction centers directly in vivo and also in BChl–protein particles isolated from purple bacteria.
3) The RC complexes and the major antenna complexes LH1 and LH2 of purple bacteria have been successfully crystallized. Atomic structures have been precisely established in these crystals using X-ray crystallographic analysis. The pioneering works of the German scientists Deisenhofer, Michel, and Huber for determination of the atomic structure of RC from the purple bacterium Rhodopseudomonas viridis were awarded the Nobel Prize in Chemistry in 1988.
In purple bacteria, BChl molecules are situated within the basic light harvesting-1 (LH1) antenna complexes, 30-32 molecules around each RC [18, 20]. In addition to LH1, many bacteria also have auxiliary antenna complexes LH2. Usually there are 1-2 LH2 complexes per RC, but under poor illumination their number can reach 4-5. In the LH1 and LH2 complexes, BChl molecules within thin (about 40 Å) phospholipid membranes are organized with specific transmembrane polypeptides as regular circular structures.
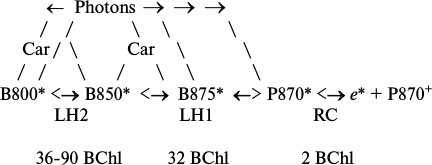
The SEE migration in purple bacteria from the antenna mass to the RC is realized through inductive resonance mechanisms [21, 22] according to the following general scheme [23, 24] (Fig. 1).
Fig. 1. Scheme of SEE migration and trapping in purple bacteria. Car, carotenoid molecules; fractions B800, B850, B875, and P870 are produced by chemically identical BChl-a molecules, and their spectral shifts are caused by differences in the BChl bonds with the polypeptide carriers and its self-association; P870 is a special BChl pair within the RC from which an excited electron (e*) enters the chain of transmembrane molecular carriers; the figures in the lower row show numbers of molecules in separate spectral groups per RC; the signs <→, ←> mean that the SEE or electron are transferred into both sides, but more efficiently in the direction indicated with the thick arrow.
The terminal migration stage B875* ←> P870* is the main bottleneck in the chain of SEE delivery to the RC. In this stage, the migration of the SEE is associated with two serious difficulties: the existence of an entropy barrier due to the ratio B875/P870 equal to 16 and to the too great distance (45 Å) in the LH1 complexes between a circle of 16 pairs of B875 molecules and the special P870 RC pairs located in the center of the circle [25, 26]. In the light of these facts, many physicists could not agree with the statement that in this class of photosynthesizing organisms the quantum yield of the SEE delivery from dozens of BChl antenna molecules onto special pairs of RC and the subsequent efficient conversion within them could be close to unity.
To analyze the energy migration efficiency, the fundamental theory of inductive resonance by Förster [21, 22] seems to be fitting. According to this theory, statistics of SEE transfers from an excited donor molecule (D*) onto an acceptor molecule (A) in general is described by the following formulas:
kD,A = (tD,A)–1 ~ f(φAB,ψA,ψD)2 (Rcr/LD,A)6 n–4 τR–1 ∫FD(ν) εA(ν) ν–4 dν, (1)
(Rcr)6 ~ 2/3(n–4 τR)–1 ∫FD(ν) εA(ν) ν–4 dν, (2)
where kD,A is an averaged rate constant of the SEE transfer from D* to A; tD,A by determination is the average time of this transfer; f(φAB,ψA,ψD)2 = [cosφAB – 3cosψA cosψD]2 is a factor of mutual position of dipole transition moments of the D* and A* molecules on their transitions between the basal and lower excited states; φAB, ψA, and ψD are angles between these dipoles [21]; Rcr is the critical distance of the SEE migration from D* onto A at the constant kD,A value equal to the sum of intramolecular constants of SEE deactivation in D* molecules, the Rcr value being determined in chaotic three-dimensional ensembles of molecules with mean value of the factor ξ(φ,ψ,θ)2 = 2/3 [21]; τR is the radiation lifetime of BChl; LD,A is the distance between centers of chromophores of the donor and acceptor molecules; n is the light refraction coefficient in the medium; τD is the SEE lifetime (or fluorescence) of the donor molecules; FD(ν) and εA(ν) are the normalized fluorescence spectrum of the donor and the absorption spectrum of the acceptor; according to the Einstein’s law [27], the expressions ∫FD(ν) dν/τr ν3 and ∫εA(ν) dν/ν are proportional to oscillator forces, or otherwise, to dipole transition moments for singlet transitions D*→D and A→A*; ν is an optical frequency in cm–1. Note that the formulas (1) and (2) were deduced on the assumption that the distances between centers of the dipoles D→D* and A→A* were significantly greater than their effective lengths.
We will analyze below the specifics of all factors included in the basic formula (1) in vivo. We will compare the SEE migration rates in purple bacteria with the migration in chaotically located BChl monomers at similar distances between the chromophores.
Orientation factor f(φAB,ψA,ψD)2. The dipole transition moments (further in the text referred to as “dipoles”) of BChl molecules involved in the circular LH1 complexes are located within membranes nearly in a single plane [28, 29]. The mean value of this factor for two-dimensional chaotic ensembles of molecules is known to be higher than for three-dimensional chaotic ensembles (2/3). Therefore, in purple bacteria in the ensembles of B875 antenna dipoles the fraction of disadvantageous positions decreases with respect to dipoles of the P870 special pairs of RC. Because of ultrafast energy migration along the B875 ring, the SEE from molecules with the dipoles situated unsuccessfully relative to P870 enter virtually instantaneously into B875 molecules with the successfully located dipoles, which optimizes the migration from the B875* complex onto the P870 pair.
Factor LD,A. As mentioned above, distances between the centers of chromophores of the B875 antenna molecules and the P870 special pair of RC are very great and reach 45 Å [25, 26]. However, there is also a positive consequence: all molecules B875 in the LH1 structure are able to directly deliver SEE onto the P870 special pair located in the center of their circle.
Factor n–4. The use by Förster of the light refraction coefficient n in formulas (1) and (2) was quite adequate for homogenous liquid and solid solvents of dyes that were used in studies of energy migration. However, this parameter does not have a physical sense in membranes of dozens of Å thickness. Therefore, in the case of photosynthesis, n–4 in formulas (1) and (2) has to be replaced by the dielectric permeability coefficient (χ2 = n4) [30, 31] in the nearest microenvironment of the donor and acceptor molecules. According to numerous literature data, in different proteins the factor χ is ~ 3.0 [32]. Obviously, for the SEE in vivo the migration values χ are important in the case of location of BChl molecules in a particular medium and on the time intervals specific for separate migration acts, i.e. on frequencies where only the small electron mass can react to rapid changes in the fields [33].
The interior of the membrane containing in purple bacteria the B875 and P870 molecules consists of approximately equal transmembrane parts of proteins and phospholipid tails. The specificity of the membrane protein primary structures discovered by Prof. Zuber is extremely important: their transmembrane α- and β-helices contain virtually no aromatic and polar amino acids (they are concentrated in the terminal chains that extend from the membrane) [34, 35]. The phospholipid tails forming another component of the mass of membranes also are very hydrophobic. Thus, the interior of membranes mainly consists of nonpolar lipidic groups. Correspondingly, their electrons on single chemical bonds have minimal ability for polarization.
In the reference book [36], the light refraction coefficient (n) values for most nonpolar chemical compounds are within 1.28 ≤ n ≤ 1.31, and from the formula χ = n2 it follows that their minimal values of χ are very small, 1.64 ≤ χ < 1.72.
In our work [31] the χ value was evaluated for hydrophobic fragments of RC polypeptides around the P870 special pair. On consideration of small amounts of bound water, for the minimal χ of the medium the χ factor in the internal layer of about 20 Å with the gradient from the center to periphery was found to be in the limits of 1.65-1.78 [31]. Considering the influence of the P870 molecules themselves, for the more likely parameter of the medium χ = 1.72 this value occurs in the limits of 1.65-2.00.
Optical frequencies. The optical frequency (ν–4) plays an important role in formulas (1) and (2). On comparison with BChl B800 monomers in vivo, the frequency of the long-wavelength band in B875 molecules is 9% lower that under other equal conditions increases approximately by 42% the migration rate constant according to formula (1). On comparison with typical dyes such as acridine, fluorescein, rhodamine, etc., this gain is about 400%.
Bacteriochlorophylls seem to be the red-most natural dyes. In a neutral organic medium, the long-wavelength absorption band of BChl-a has a maximum near 770 nm. It is important that it can be easily shifted to the “red” region of the spectrum. Even BChl-a monomers in the antenna complexes of LH2 have peaks at about 800 nm due to bonds with the carrying polypeptide chains. The BChl-a pair complex in LH2 has peaks at about 850 nm and in LH1 at about 875 nm, also due to the bond with the carrying polypeptides plus strong bonds in the pairs and with neighboring pairs in the circular structures. Such a train of absorption bands enlarges the spectrum of active absorption of solar energy and brings its red boundary in purple bacteria up to 910-920 nm on the basis of BChl-a and up to 1030-1040 nm on the basis of BChl-b. This boundary is rather close to the optimal boundary for all energy systems of the photoelectric type. Upon the selective absorption of solar radiation by the atmosphere, the optimal boundary on the surface of our planet is close to 1050 nm [37, 38].
Spectral overlap integral ∫FD(ν) εA(ν) ν–4 dν. Chromophores of the P870 pairs are located closer to each other than chromophores of α/β pairs of B875, which results in a virtual coincidence of the 0–0 transitions in their long-wavelength absorption bands. Consequently, the overlap degree of the B875 fluorescence and the P870 absorption spectra in formula (1) reaches 87% of the maximum, resulting theoretically in matching the peaks of these spectra [39].
Excitons. At the above-indicated distances between the centers of neighboring chromophores of molecules of P870 (7.5 Å) and B875 (9 Å) [26, 31], values of their interaction energies reach ten meV. In such associates excitons arise: in the RC the SEE includes a pair of P870 and in the LH1 chains it includes 4-6 neighboring molecules of B875 [40, 41]. It is known from physics that in associates including z identical interacting molecules, the long-wavelength absorption band is split into z separate bands. And the sum of dipoles of these bands is retained, i.e. it is approximately equal to the sum of dipoles of z monomers of the corresponding molecules. In the LH1 complexes of purple bacteria, because of the circular symmetry of B875 molecules the majority of these bands are forbidden, and thus only two bands with the wave vectors k = ±1 remain [40, 41]. The mutual position of dipoles in the neighboring molecules of P870 and B875 provides for the domination of the long-wavelength bands. According to calculations, at real mutual spectral positions of the absorption bands in the B875 complexes and P870 pairs the ratio of the forward and reverse constants of SEE migration in the region of B875* ←> P870 has to increase 3 < δ < 4 times [42]. In special pairs of RC from the bacterium Rhodobacter sphaeroides, the long-wavelength band near 870 nm is occupied by approximately 85% of the strength of the sum of dipoles of two molecules. On SEE migration, the BChl associates with delocalized exciton can be considered as individual molecules. This idea is confirmed by experimental data of Razjivin et al. [43] that in the Rhodospirillum rubrum chromophores, after the exciting pulse the B875 band bleaching calculated per absorbed photon is 4-5 times greater than the bleaching corresponding to the BChl monomer. The exciton effect also significantly increases the SEE migration rates between B875* and P870, because, according to the theory of this phenomenon [21, 22], their amplitudes are proportional to the product of dipoles of the interacting molecules.
Comparison by formula (1) of the migration rates between chaotically distributed in space BChl B800 monomers in protein medium and between the B875 and P870 complexes in vivo indicates that the total gain from all the above-listed factors for values of these constants at SEE migration from B875* onto P870 is 100-200. Because of this, the efficient constant value of the SEE migration from the B875 complexes onto the P870 pairs reaches in vivo several dozens of inverse picoseconds [44].
COUPLING OF MIGRATION WITH SUBSEQUENT ENERGY TRAPPING AND
CONVERSION IN REACTION CENTERS. GROSS QUANTUM YIELD
The ultrafast migration of SEE from the B875* antenna molecules onto the P870 pairs in the RC still does not solve the problem of efficient photosynthesis, because SEE can be returned from P870* onto B875 through the same mechanism. Let us perform approximate calculations based on experimental data on the SEE migration and trapping in purple bacteria.
Data of Godik [45] and Katiliene et al. [46] have shown that the rate of trivial SEE deactivation in the B875 antenna complexes is ~(650 ps)–1. To provide the quantum yield of SEE trapping in the RC to be about 90%, the rate of this trapping has to be at least an order of magnitude higher, i.e. ~(65 ps)–1. Considering that 16 pairs of B875 correspond to each P870 pair in the RC, let us assume that the rate of reverse migration of the SEE from P870* onto B875 can be 16-fold greater, i.e. ~(4 ps)–1. Up to now, in many reviews it is stated that the rate of the SEE primary trapping in the RC of purple bacteria is ~(3 ps)–1. Such rate of SEE trapping and the ratio 1 : 16 of the rates of forward and reverse migrations result in the quantum yield (QY) of the trapping to be ~0.65, even on assuming the irreversibility of this trapping.
This discrepancy is significantly removed due to above-mentioned features of excitons [40], which increase 3-4 times the ratio of migration rates, and to new kinetic data for RC obtained in the pioneering works of Shuvalov’s laboratory.
In the works of Shuvalov [47, 48], the RC state was recorded with the transfer of an excited electron onto P800 with a small loss of energy and a very short lifetime of ~1 ps. In subsequent works of Shuvalov et al. [49, 50], the first excited state of the RC was detected within ~0.2 ps. It seemed to be charge transfer complexes (CTC) in the P870 pairs in which noticeable electric dipoles were produced. In the field of such a dipole, a specific water molecule was polarized between the P870 dipoles [51], along with quenching up to 0.02 eV of the SEE energy [52, 53].
Based on the above-presented kinetic data on the SEE migration in the LH1 complexes and their trapping in the RC of purple bacteria, a model was designed describing the succession of the migration primary processes and energy trapping in the LH1 complexes of purple bacteria. From this model (presented below), the quantum yield value of photosynthesis was determined for these organisms.
MODEL OF PRIMARY PROCESSES FOR PURPLE BACTERIA
In the model presented in Fig. 2, the electron transfer from H760– onto QA with constant ke3+ ≈ (200 ps)–1 is virtually irreversible because the energy difference between these states is close to 0.55 eV [52, 53]. The subsequent electron transfers from QA– onto the quinone pool dissolved in the membrane occur within dozens of milliseconds. These transfers are determined by the rate of quinone diffusion and limit the real carrying capacity of the electron transport chain in purple bacteria. The charge deficiency arising in the special P870+ pair upon the electron transfer is compensated by the RC-bound molecule of a heme-containing protein, cytochrome c (P870+ + Cyt-c → P870 + Cyt-c+), and within approximately two microseconds after that the RC is able to function again.
Fig. 2. Scheme of primary processes in purple bacteria. B875* is the excited state in the B875 antenna molecules that can migrate onto a special P870 pair of an RC with averaged constant δ km ≈ (35 ps)–1 [17, 40, 42] at the reverse constant 16 km. In P870* the state {CTC±}* (abbreviation for Charge Transfer Complex) is produced with the constant kCTC+ = (0.2 ps)–1 [47, 48]; {P800– P870+} is the RC state after the first electron transfer onto P800 with constant ke1+ = (3 ps)–1 [45, 46]; {H760– P870+} is the RC state after the secondary transfer of the electron onto bacteriopheophytin with the constant ke2+ = (1 ps)–1 [45, 46]; P870+ QA– is the RC state after the third, irreversible electron transfer with constant ke3+ = (200 ps)–1 [2, 4, 42]; kCTC–, ke1–, and ke2– are rate constants of the reverse transfers; kw,A, kwP870*, kwCTC, kwP800, and kwH760– are rate constants of deactivations of the corresponding states in the RC.
All relay-race transfers of SEE and electrons occur in BChl complexes fixed in the membranes, and they therefore can be modeled using first order balanced differential equations. The model for the SEE migration processes and their conversion in the purple bacteria RC is presented below.
In these primary stages, all processes are 99.99% finished within 1.5 ns; therefore, the influence of slower processes of electron transfer in the subsequent stages Cyt-c → P870 and after {QA–} can be neglected. On the modeling, SEEs were initially given to the B875 and P870 complexes in the ratio of 16 : 1. The major fraction of SEEs from B875* successfully reaching P870 was converted within it into separate charges with different sign. After three stages of the transfer, electrons dislodged from P870 in the state {CTC±}* reached bound ubiquinone {QA}. Their fraction rather accurately corresponds to the value of effective quantum yield in purple bacteria.
Now it is necessary to introduce the correction factors and values of some constants. The correction by average values of the factors f(φAB,ψA,ψD)2 in vivo and in chaotic ensembles of molecules 0.95 : 2/3 = 1.425. The correction is performed by the absorption peaks of B875 and B800: these peaks in Rhodobacter sphaeroides at 810 and 864 [50] are given by the ratio (864/810)6 = 1.443 [54].
The modeling has shown that the most important constant is km. The distances between the centers of B875 and P870 chromophores are 45.3 Å [25, 26]. At such distance it is reasonable to use Förster’s fundamental theory of inductive resonance. Let us write formula (1): a) for our case, and b) in a special form for the chaotic ensemble B800, when LD,A = Rcr and τD = τR. Then for (b) by the definition: kD,A = (τR)–1 and ξD,A(ψ,θ1,θ2)2 = 2/3. The division each against the other, respectively, the left and right parts of these factors with the correction factors, will result in the known Förster expression:
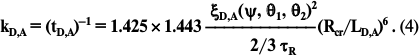
For the major spectral fraction of the purple bacteria pigment BChl-a B875, the Rcr values on the SEE migration in photosynthetic membranes were found to be 80 Å [55] and 78.8 Å by an independent method [31]. Their mean value for the wavelength 875 ± 5 nm is Rcr = 79.5 ± 2 Å. From the literature the radiative lifetime of BChl is known to be τR = 18 ± 2 ns [56]. The effective value ξD,A(ψ,θ1,θ2)2 for case (a) is close to 0.95, because due to the ultrafast migration along the B875 ring the SEE rapidly reaches the B875 α/β-pairs located optimally relative to P870. Place these data formally into formula (4):
During the SEE migration, let us use the exciton factor described in the first part of this work according to which the ratio of the forward and reverse constants of B875 ←> P870 migration is 16 : δ ≈ 4.6. Taking into account that the strength of the long-wavelength dipole P870 ≈ 84% of the sum of dipoles of two BChl molecules producing P870 [54], this factor in them is to be increased 1.68-fold. Similarly for excitons involving 4-6 ≈ 5 B875 molecules, this factor is approximately equal to 4 [24, 43]. These factors together increase 7-fold the values of the migration constants δ km and 6 km in Eqs. (3a) and (3b), which results in the following evaluation:
kD,A = (tD,A)–1 = 33.2 × 109 s–1. (4b)
However, under the actual redox potentials of the medium in vivo, the fraction of photoactive RCs is 85-90% (the other 10-15% inactive P870 quench the SEE with rate of (40-50) × 109 s–1 [45, 57]). This decreases, respectively, the coefficients at the efficient members in Eqs. (3b) and (3c) and increases the overall coefficient at the factors of the losses kwP870 and kwCTC. The final result is:
and the reverse constant on consideration of the exciton effect is:
The system of Eqs. (3, a-f) was solved using the RKGS computer program developed by A. V. Vinogradov [58]. Values of constants of reverse transfers (kCTC–, ke1–, ke2–) were taken from the works of Shuvalov [57] and of Holzwarth and Muller [59]. Kinetics were obtained for the SEE in B875 and all states in the RC from the moment of excitation up to 1.5 ns, and the SEE quantity that finally occurred in the efficient channel and the channel of losses. They correspond to the yields as follows:
Effective quantum yield QY(ph) ≈ 0.887;To assess the efficiency of the energy migration organization in purple bacteria, values of quantum yields were calculated under conditions of conventional decrease in the distance between B875 molecules and P870 pairs of RCs. The decrease was modeled by the growth of the SEE transfer constants between B875 and P870 on retention of their ratio. Even a 10-fold increase in the rates of km and δ 16 km resulted in a rather weak gain in the effective quantum yield value: 0.887 → 0.892. Thus, the SEE migration is organized close to optimal for the antenna of 32 BChl molecules per RC and interchromophore distances between BChl in the LH1 complexes in vivo.
Quantum yields of losses:
in the B875* antenna complex: QY(w,A) ≈ 0.086;
in the special P870* pair: QY(w,P) ≈ 0.027;
total losses: QY(Sw) ≈ 0.113.
DISCUSSION
As shown above, the main quantum losses occur in the BChl antenna fraction B875. Analysis of dependence of these parameters on variations of values of the acting constants revealed that the quantum losses are mainly determined by the constant of the losses in B875, kw,A, and the ratio of the forward and reverse migration constants between B875 and P870.
Excluding from consideration of ultrapure crystals, among numerous data of physics and photochemistry on intramolecular migration of energy no precedents are known of efficient deliveries of SEE from large masses of molecules onto a single center. The efficient deliveries are realized only in natural photosynthesis due to the unique feature of membrane proteins, which produce unique in vivo cellular structures. Within such structures chlorophyll molecules at a concentration lower than molar are arranged in a manner virtually preventing immediate contacts of their chromophores (!). But the mutual positions of neighboring chromophores promote the domination of long-wavelength bands optimal for the SEE migration in the spectra of absorption bands split by the electromagnetic interaction. These unique properties of transmembrane protein chains provide high rates of migration under conditions of virtual absence of quenching dimers in the mass of antenna chlorophylls. Note that in liquid and solid solutions of chlorophylls the production of quenching dimers begins already at the concentration of about 1-3 mM. In purple bacteria the distances between the chromophore centers in the P870 and B875 complexes are 7.5 and 9 Å [26], which corresponds to local concentrations of this pigment of about 0.5 M. At such distances the migration acts occur with rate more than 1012 s–1 (!) and the chromophore interactions in the neighboring BChl is sufficiently strong for generation of excitons.
The structure of antenna BChl in photosynthetic membranes organized by the intramembrane parts of proteins provides effective delivery of SEE from the antenna BChl to the reaction centers. This structure is a basis of the effective energetics in photosynthesizing organisms and the most significant achievement in the evolution of living Nature on Earth.
And a complex of fundamental scientific and technological problems emerges in the field of applied solar energetics: to invent something similar to a multilayer photoelectric film from cheap stable polymers and dyes with infrared absorption boundary based on achievements of modern nanotechnology.
In the monograph The Nanotechnology Revolution by Drexler and Peterson, the authors compare the level of our modern technologies with the “industrial basis” of natural photosynthesis. They write [60]:
“Industry-as-we-know-it takes things from nature—ore from mountains, trees from forests—and coerces them into forms that someone considers useful. Trees become lumber, then houses. Mountains become rubble, then molten iron, then steel, then cars. Sand becomes a purified gas, then silicon, then chips. And so it goes. Each process is crude, based on cutting, stirring, baking, spraying, etching, grinding, and the like.
Trees, though, are not crude: To make wood and leaves, they neither cut, grind, stir, bake, spray, etch, nor grind. Instead, they gather solar energy using molecular electronic devices, the photosynthetic reaction centers of chloroplasts. They use that energy to drive molecular machines—active devices with moving parts of precise, molecular structure—which process carbon dioxide and water into oxygen and molecular building blocks. They use other molecular machines to join these molecular building blocks to form roots, trunks, branches, twigs, solar collectors, and more molecular machinery.
Every tree makes leaves, and each leaf is more sophisticated than a spacecraft, more finely patterned than the latest chip from Silicon Valley. They do all this without noise, heat, toxic fumes, or human labor, and they consume pollutants as they go. Viewed this way, trees are high technology. Chips and rockets aren't”.
It is difficult to argue against this conclusion.
REFERENCES
1.Borisov, A. Y. (1978) Mol. Biol. (Moscow),
12, 267-275.
2.Borisov, A. Y. (1979) in Photosynthesis in
Relation to Model Systems (Barber, J., ed.) Elsevier Sci. Publ.
Corporation, Amsterdam-New York-Oxford, pp. 1-26.
3.Krasnovsky, A. A. (1948) Dokl. Akad. Nauk
SSSR, 60, 421-424.
4.Krasnovsky, A. A., and Voinovskaya, K. K. (1951)
Dokl. Akad. Nauk SSSR, 85, 389-392.
5.Krasnovsky, A. A. (1960) Ann. Rev. Plant
Physiol., 11, 363-410.
6.Terenin, A. N. (1943) Acta Phys. Chem.,
18, 210-214.
7.Chibisov, A. K. (1969) Photochem.
Photobiol., 10, 331-347.
8.Dmitrievsky, O. D., Ermolaev, V. L., and Terenin,
A. N. (1957) Dokl. Akad. Nauk SSSR, 114, 75-78.
9.Brody, S. S., and Rabinowich, E. (1957)
Science, 125, 555-556.
10.Krasnovsky, A. A., Jr. (1994) Proc. Roy. Soc.
Edinburgh, 1028, 219-235.
11.Borisov, A. Y., and Godik, V. I. (1970)
Biochim. Biophys. Acta, 223, 441-443.
12.Borisov, A. Y., and Godik, V. I. (1972) J.
Bioenerg., 3, 211-220.
13.Borisov, A. Y., and Godik, V. I. (1972) J.
Bioenerg., 3, 513-523.
14.Paschenko, V. Z., Kononenko, A. A., Protasov, S.
P., Rubin, A. B., Rubin, L. B., and Uspenskaya, N. Y. (1977)
Biochim. Biophys. Acta, 461, 403-412.
15.Campillo, A. J., Hyer, R. C., Monger, T. G.,
Parson, W. W., and Shapiro, S. L. (1977) Proc. Natl. Acad. Sci.
USA, 74, 1997-2001.
16.Borisov, A. Y. (1973) Current Problems of
Photosynthesis [in Russian], MGU Publishers, Moscow, pp.
164-173.
17.Borisov, A. Y. (1976) Mol. Biol. (Moscow),
10, 460-465.
18.Cogdell, R. J., Gardiner, A. T., Roszak, A. W.,
Law, K. J., Sauthall, J., and Isaaks, N. W. (2004) FEBS Lett.,
555, 35-39.
19.Robert, B., Cogdell, R. J., and van Grondelle, R.
(2003) in Advances in Photosynthesis and Respiration (Green, B.
R., and Parson, W. W., eds.) Dordrecht, pp. 169-188.
20.Roszak, A. W., Howard, T. D., Southall, J.,
Gardiner, A. T., Law, K. J., Isaaks, N. W., and Cogdell, R. J. (2003)
Science, 302, 1969-1972.
21.Förster, T. (1960) in Comp. Effects of
Radiation (Kirby-Smith, J. S., and Magee, J. L., eds.) John Wiley
& Sons, New York, pp. 300-341.
22.Agranovich, M. V., and Galanin, M. D. (1978)
Transfer of Electron Excitation Energy in Condensed Media [in
Russian], Nauka, Moscow, pp. 23-41.
23.Borisov, A. Y. (1987) Biofizika,
32, 1046-1061.
24.Borisov, A. Y. (1989) Photosynth. Res.,
20, 35-58.
25.Hu, X., Damjanovic, A., Ritz, T., and Schulten,
K. (1998) Proc. Natl. Acad. Sci. USA, 85, 5935-5941.
26.Brookhaven Protein Bank (http://www.rcsb.org/pdb/, identification n-r 1LGH
and PQS bank).
27.Einstein, A. (1917) Phyz. Zeit.,
18, 121-127.
28.Abdourakhmanov, I. A., Ganago, A. O., Erokhin, Y.
E., and Solov’ev, A. A. (1979) Biochim. Biophys. Acta,
546, 183-186.
29.Koepke, J., Hu, X., Muenke, C., Schulten, K., and
Michel, H. (1996) Structure, 4, 591-598.
30.Knox, R. S., and van-Amerongen, H. (2002) J.
Phys. Chem., 106, 5289-5293.
31.Borisov, A. Y. (2010) Biol. Membr.
(Moscow), 27, 1-4.
32.Pitera, J., Falta, M., and van Gunsteren, W. F.
(2001) Biophys. J., 80, 2546-2555.
33.Borisov, A. Y. (2013) Optika i
Spektroskopiya, 114, 67-72.
34.Zuber, H., Brunisholz, R., and Sidler, W. (1987)
in Photosynthesis (Amesz, J., ed.) Elsevier, Amsterdam, pp.
233-271.
35.Zuber, H. (1987) in The Light Reactions,
Chap. 5 (Barber, J., ed.) Elsevier Sci. Publ., Amsterdam, pp.
198-243.
36.Handbook of Chemistry and Physics, 67th
Edn. (1986) CRC Press, pp. 2424-2467.
37.Ross, R. T., and Hsiao, T. L. (1978) J. Appl.
Phys., 48, 4763-4785.
38.Rabek, J. (1985) Experimental Methods in
Photochemistry and Photophysics, Vol. 1 [Russian translation]
(Borisov, A. Y., ed.) Mir, Moscow, pp. 40-47.
39.Borisov, A. Y., and Gaidukova, A. P. (2009)
Biol. Membr. (Moscow), 26, 31-39.
40.Hu, X., Damjanovic, A., Ritz, T., and Schulten,
K. (1997) J. Phys. Chem. B, 101, 3854-3871.
41.Novoderezhkin, V. I., Monshower, R., and van
Grondelle, R. (1999) Biophys. J., 77, 666-681.
42.Novoderejkin, V. I., and Razjivin, A. P. (1994)
Photosynth. Res., 42, 9-15.
43.Razjivin, A. P., Borisov, A. Y., Gadonas, R. A.,
Danielius, R. V., and Piskarskas, A. S. (1982) FEBS Lett.,
143, 40-43.
44.Van Grondelle, R., and Somsen, O. J. G. (1999) in
Resonance Energy Transfer (Andrews, D., and Demidov, A., eds.)
John Wiley and Sons, New York-Brisbein-Toronto, pp. 366-391.
45.Godik, V. I., and Borisov, A. Y. (1977) FEBS
Lett., 82, 355-358.
46.Katiliene, Z., Katilius, E., and Woodbury, N. W.
(2003) Biophys. J., 84, 3240-3251.
47.Shuvalov, V. A., Sharkov, A. V., Matveetz, Y. A.,
and Krukov, P. G. (1978) FEBS Lett., 91, 135-139.
48.Shuvalov, V. A., and Yakovlev, A. Y. (1998)
Membr. Cell. Biol., 12, 1276-1285.
49.Khatynov, R. A., Khmelnitsky, A. Y., Leonova, M.
M., Vasil’eva, L. G., and Shuvalov, V. A. (2008) Dokl. Akad.
Nauk. SSSR, 422, 835-840.
50.Khatynov, R. A., Khmelnitsky, A. Y., Khristin, A.
M., and Shuvalov, V. A. (2010) Dokl. Akad. Nauk. SSSR,
430, 416-420.
51.Borisov, A. Y., and Kuznetsova, S. A. (2002)
Biochemistry (Moscow), 67, 1224-1229.
52.Borisov, A. Y., and Fok, M. V. (1999) Biochem.
Mol. Biol. Int., 47, 117-125.
53.Borisov, A. Y. (2004) Biochemistry
(Moscow), 69, 813-817.
54.Mikhailjuk, I. K., Knox, P. P., Paschenko, V. Z.,
Zakharova, N. I., Tusov, V. B., and Razjivin, A. P. (2005)
Biophysics (Moscow), 50, 668-675.
55.Clayton, R. K. (1980) Photosynthesis. Physical
Mechanisms and Chemical Patterns, Cambridge University Press,
Cambridge-New York-Melbourne, pp. 47-49.
56.Connolly, J. S., Samuel, E. B., and Janzen, A. F.
(1982) Photochem. Photobiol., 36, 565-574.
57.Shuvalov, V. A. (2000) Transformation of the
Solar Energy in the Primary Act of Charge Separation in the
Photosynthesis Reaction Centers [in Russian], Nauka, Moscow, pp.
15-19.
58.Borisov, A. Y., and Vinogradov, A. V. (1992)
Biol. Membr. (Moscow), 9, 420-431.
59.Holzwarth, A. R., and Muller, M. G. (1996)
Biochemistry, 35, 11820-11833.
60.Drexler, K. E., and Peterson, C. (1991)
Unbounding the Future. The Nanotechnology Revolution, Quill,
William Morrow, New York, p. 9.