From Localized Excited States to Excitons: Changing of Conceptions of Primary Photosynthetic Processes in the Twentieth Century

---

R. Y. Pishchalnikov^1,2 and A. P. Razjivin^1*

¹Lomonosov Moscow State University, Belozersky Institute of Physico-Chemical Biology, 119992 Moscow, Russia; fax: (495) 939-3181; E-mail: razjivin@belozersky.msu.ru; razjivin@gmail.com

²Prokhorov General Physics Institute, Russian Academy of Sciences, Wave Research Center, ul. Vavilova 38, 119991 Moscow, Russia; fax: (499) 135-0270; E-mail: rpishchal@kapella.gpi.ru

^* To whom correspondence should be addressed.

Received November 22, 2013; Revision received December 13, 2013

---

A short description of two theories of the primary photosynthetic processes is given. Generally accepted in 1950s-1990s, the localized excited states theory has been changed to the modern exciton theory. Appearance of the new experimental data and the light-harvesting complex crystal structure are reasons why the exciton theory has become important. The bulk of data for the old theory and outstanding experiments that have been the driving force for a new theory are discussed in detail.

---

KEY WORDS: photosynthesis, energy transfer, excitons, light-harvesting antenna, Redfield’s theory

DOI: 10.1134/S0006297914030109

Abbreviations: (B)Chl, (bacterio)chlorophyll; GA, genetic algorithms; LH1, core light-harvesting complex; LH2, peripheral light-harvesting complex; PS1, photosystem 1; PS2, photosystem 2; RC, reaction center.

Many years ago, I several times visited the Bach Institute of Biochemistry of USSR Academy of Sciences. I was going to meet with “our” Academician (supervising photosynthesis) A. A. Krasnovsky. It was a time in the early 1980s, when we began to get amazing results on chromatophores and light-harvesting complexes of purple bacteria by means of differential absorption picosecond spectroscopy. Articles for publication in the Proceedings of the USSR Academy of Sciences had to get a recommendation of an academician. Alexander Abramovich listened to my confused explanations, kindly asked two or three questions, and wished further success...

(A. P. Razjivin)

It is believed that early studies of photosynthesis were performed by Priestley ​​more than 300 years ago. Research works of direct relevance to contemporary views on photosynthesis date to the first half of the twentieth century. After World War II, the intensity of these studies increased substantially, and in 1950-60s a sufficiently complete theoretical model (paradigm) of light energy conversion during photosynthesis was created [1, 2]. In the next 30 years experimental studies have brought many new results, but the theoretical picture of the primary (physical) processes of photosynthesis was not fundamentally changed, but only became more elaborate. The best description of this theoretical model is given, in our opinion, by A. Yu. Borisov ([3] and his other papers). Part of the experimental results obtained during this period did not fit the widely accepted theoretical model. But all the researchers did not seem to notice these results. Finally, laser absorption measurements in the 1980s [4-7] allowed questioning the basic tenets of the dominant theoretical model and proposal of a new (exciton) model [8-10] (at least for the photosynthetic purple bacteria). After two or three years, an X-ray structure was obtained for LH2 complex [11, 12] that was fully consistent with the proposed new model (special inspection was performed [13]). It became clear that the theoretical picture of the primary processes of photosynthesis must be based on a quantum mechanical (exciton) representation [14-18].

THEORY OF LOCALIZED EXCITED STATES

By the 1950s and early 1960s, experimental material had accumulated that allowed researchers to formulate ideas about the structure of the photosynthetic apparatus and its operation [1, 19-22].

The first ideas were connected with the experimental data of Emerson and Arnold [23, 24] devoted to the measurement of the release of oxygen by cells of the green alga Chlorella pyrenoidosa under short light flashes and their interpretation Gaffron and Wohl [25, 26]. The result is a vision of a “photosynthetic unit” as a set of about 2000 chlorophyll molecules interacting with a separate “reaction center” in the energy harvesting process. If you use the modern terminology, we can say that the photosynthetic unit consists of the reaction center (RC) and light-harvesting antenna of chlorophyll molecules.

It was known that the photosynthetic apparatus is located in the intracellular membrane structures (in chloroplasts of plants and in bacterial chromatophores). They contain the main photosynthetic pigment chlorophyll (Chl) or bacteriochlorophyll (BChl).

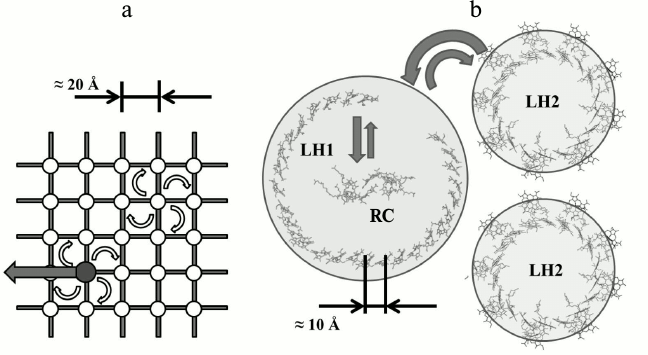
In the 1930-40s the structure of chloroplasts from cells of several plants were studied using optical and electron microscopy [27]. The electron microscopic studies of the photosynthetic apparatus showed that Chl molecules are located in the chloroplasts in the form of thin plates or layers, the thickness of which is commensurate with the size of the porphyrin moiety of Chl [28]. Before this it was known that it is possible to obtain Chl monolayers in two forms: amorphous and crystal [28, 29]. In the crystalline monolayer the Chl long-wavelength absorption maximum is approximately at 735 nm instead of about 660 nm as in solution. Since Chl in living cells has an absorption maximum of about 675-680 nm, then, apparently, they do not form Chl crystalline monolayers (and moreover, three-dimensional crystals, for which the absorption maximum is shifted to 740 nm) and is located in the chloroplasts in amorphous monolayers. The total value of the layer surface is approximately equal to that of Chl area that would have occupied by Chl contained in the chloroplast if this Chl would be uniformly distributed in the monolayer. In this case the area per molecule is within 100-200 Å, which is approximately equal to the area occupied by the flat chromophore “head” of the Chl molecule [22, 30]. This led to the estimation of the distance between the centers of adjacent BChl chromophores in a layer of ~ 20 Å (figure).

a) Model of light-harvesting antenna of purple bacteria that dominated the 1960-80s until the availability of X-ray data. White circles mark nodes of a hypothetical lattice in which BChl molecules are placed. The dark circle is a RC. Energy migration from one molecule to another has discrete character and is described according to the incoherent Forster theory [31] (white arrows correspond to resonant excitation transfer from one BChl molecule to another). Reaching the RC, the electronic energy of the excited state can be transformed into chemical energy (black arrow) or return back to the antenna. The estimated size of the unit lattice is 20 Å. b) X-ray data of light-harvesting complexes LH1, LH2, and RC of purple bacteria. Due to the high symmetry of the ring, the absorption of a light quantum into the aggregated molecules produces delocalized exciton states in them [8, 32-35] (delocalization is schematically shown as circles). The structure of exciton levels of LH2, LH1, and RC is designed so that the excited states of RC are the lowest lying levels, and due to interlayer relaxation all the energy is transferred the RC. Exciton states of LH1- and LH2-complexes do not mix with each other. So-called extended Forster theory [36] describes energy transfer between the LH2 and LH1 complexes

The location of the Chl molecules in the form of a thin (monomolecular) layer was confirmed in the study of dichroism and birefringence in chloroplasts [37, 38]. Disorder transition dipole directions of BChl molecules resulted from the low degree of dichroism of BChl molecules in vivo.

Spectral studies indicate that BChl molecules are in different forms in vivo [39-48]. In the 1950s Krasnovsky et al. found that the absorption and fluorescence spectra of these pigments are similar in solid films and photosynthetic systems, and on this basis they put forward the idea that the spectral properties of Chl a, BChl a and b, and “chlorobium” of chlorophylls are determined mainly by pigment–pigment interaction (by “aggregation” of pigment molecules). This idea was later developed and supported by many studies ([39-41] and references therein). In particular, some data suggested a dimeric state of BChl molecules in antenna [49].

The conversion of energy from the physical form to the chemical form of separated charges of opposite sign occurs in RC. Further, there is a chain of redox reactions in which energy is expended on the synthesis of chemical compounds. This system operates within time interval of 10^–3 s. However, even in sunlight, each BChl molecule absorbs a photon on average once every 10^–1 s. Therefore, if the RC with its electron transport chain is linked with only one light-harvesting BChl molecule, then the system will be idle 99% of the time waiting for the absorption of the next photon. In addition, there is no place to put the system of RC with its electron transport chain (having large size) in the photosynthetic apparatus for each molecule of the light-harvesting BChl. This contradiction was resolved when it was shown that one RC interacts with many (~10²-10³) BChl molecules within the “photosynthetic unit”. Accordingly, there must be a mechanism for collecting energy from hundreds of BChl molecules to align the rate of absorption of light quanta and the rate of their energy assimilation by the system of RC with its chain of enzymatic reactions.

Two mechanisms have been proposed for how to harvest light energy absorbed by the BChl molecules and to transfer it to the RC. E. Rabinowitch wrote in 1959 [1]: “Gaffron and Wohl said that cooperation between the many light-absorbing chlorophyll molecules and a single reaction center in a unit can be attributed to the migration, either of energy-rich particles generated at each chlorophyll molecule, or of energy quanta. The second picture has fascinated workers in photosynthesis in the last 20 years, without a definite answer being found as to its relevance”.

Gaffron and Wohl [25] suggested that energy is captured after the “fluctuations” within the “unity” of 2500 molecules of Chl. Wohl said a little later [50] that the energy transfer can occur in the form of electronic excitation energy, but during this time there was no physical theory to assess the validity of the transfer. (Later, in 1947, this theory was proposed by Forster [31].)

Largely, the idea of the ​​RC and its interaction with the antenna was formed due to papers by Duysens [49, 51, 52]. If an RC gets energy through Forster’s inductive resonance mechanism, then the RC should have an absorption band close to the long-wavelength edge of the longest-wavelength absorption band of light-harvesting BChl. Duysens discovered this band (and introduced the notation P for this pigment of RC) [51, 52]. In other words, it was found that at the entry point of the RC there is approximately the same BChl molecule as light-harvesting antenna BChls or BChl dimer (“special pair” of BChl molecules).

The question whether the excitation lifetime in the antenna is consistent with the excitation efficiency of energy transfer to the RC was discussed by Frank and Teller [53]. Radiative lifetime of the excited state of Chl calculated by integrating the absorption band was 15 ns [54], and for BChl 18 ns [55]. For resonant energy transfer the lifetime of excitation on a Chl molecule should be more than 10^–12 s (approximate period of nuclear vibrations). Accordingly, it turned out that in a time of 1-2 ns excitation can make about a thousand jumps via several hundred molecules of light-harvesting Chl and be successfully captured by the RC.

The ability to determine the time of the primary charge separation in purple bacteria appeared as a result of development of RC isolation techniques by Clayton and Reed [56, 57]. The characteristic time of excitation energy capture by an RC (primary charge separation in the RC) was evaluated by the fluorescence quantum yield of the RC isolated from Rhodobacter sphaeroides cells and found to be 7 ps. Later, this time was clarified [58] and is now accepted to be 3 ps. The time of primary charge separation in cyanobacteria and higher plants is still a matter of debate [59].

So, the main characteristics of the theoretical model are as follows – a two-dimensional square matrix, the distance between nodes ~20 Å, dimer BChl – “special pair” BChl in one of the nodes, the energy transfer by mechanism of inductive resonance (a “random walk”).

What are the main features of this model? How does this model work? In schematic form the process of absorption of a photon, energy transfer to the RC antenna, and its capture by the center is the following. A light quantum is absorbed by one of the light-harvesting antenna BChl molecules, converting it to the singlet excited state. This excitation can move on the matrix from one BChl molecule to another through the inductive-resonance mechanism, which is well described by Forster’s theory. In the case of two BChl molecules, the jump time is approximately 2 ps. Each molecule has four identical molecules adjacent to it in the matrix, and therefore the excitation will be on a given molecule four times less, ~0.5 ps. Excitation motion from one matrix node to another obeys to the mathematical description of the “random walk” [60]. One of the nodes of the matrix belongs to the RC entry (“special pair” of BChl molecules of RC or P700). This node has an additional deactivation channel of excitation energy – charge separation with a time constant of about 3 ps. Arriving at the RC, the excitation can go via the charge separation channel, but significantly more likely it will return back to the antenna (in proportion to the time constants of 0.5 and 3 ps). Then the excitation random walk begins again and finishes due to charge separation in next contact with an RC unit, or due to spontaneous loss of energy, for example by fluorescence emission of a photon.

All works on photosynthesis from the late-1950s to the mid-1990s are based on the model presented above. During this time, only the degree of detail of the model was changed, and new objects for its application were found.

It should be noted that there were experimental facts that contradict the model. For example, the absence of the B800 band in the fluorescence excitation spectrum of Rhodospirillum rubrum chromatophores, which is present in the photooxidation action spectrum of RC [55, 61], indicates irreversible capture of excitations from the antenna by RC.

Several results contradicting this model have been obtained in the course of our own research on the transfer of excitation energy and its capture in chromatophores and LH1–RC complexes of purple bacteria by means of laser difference absorption picosecond spectroscopy [4-7]. These results were confirmed in other laboratories [62-64].

We made ​​several attempts to construct theoretical models for the interpretation of spectral-kinetic processes in antennas isolated from purple bacteria [7, 65], the latter being successful [8, 66, 67]. Bleaching of four or more antenna BChl molecules per absorbed light quantum was a direct indication of the cooperative response of the antenna [7] or, in other words, the delocalization of the excitation over several BChl molecules. Exciton theory [68] and, in particular, the theory of excitons in molecular aggregates [69, 70] suited to describe the observed phenomena. But its use for the calculation of the experimental spectra of the antenna containing ~30 BChl molecules required specifying the spatial orientation of these molecules and the distance (or the strength of interaction) between them. We were fortunate to determine that orientation. It was found that if the light-harvesting BChl molecules are arranged in a circular unit, symmetric with respect to the rotation axis, it is possible to obtain an adequate description of the spectral-kinetic effects [9, 10, 71].

Appearing later, the X-ray data [11, 12, 72] proved the reality of ring-shaped molecular aggregates of light-harvesting BChl in LH1 and LH2 complexes from purple bacteria cells. Since that time, descriptions of transfer and trapping of excitation energy in bacterial photosynthesis based on exciton representations became common [14-18].

Modern models of primary photosynthetic processes are inseparably linked with the quantum-mechanical approach. This is because the distance between the BChl molecules of the long-wavelength band in the light-harvesting pigment–protein complexes is two times less than previously thought (~10 Å [73] instead of ~20 Å). At such distance an exciton interaction between BChl molecules becomes some hundreds cm^–1, which leads to excitation delocalization over several BChl molecules. Experimental data of recent years have shown that the excitonic effects are identified in the study of all primary processes of photosynthesis [74-85]. Particularly important were the results of the spectroscopy of single complexes [79-82] and long-lived quantum coherence in the electronic light-harvesting complexes [83]. In subsequent studies of Scholes et al. [84] and Engel et al. [85] the preservation of quantum coherence was confirmed even at room temperature.

EXCITON THEORY IN PHOTOSYNTHESIS

Let us consider in detail the features of the theoretical method used in the description of the primary processes of photosynthesis. First of all, it is worth noting that the results of our experimental studies [4-7] refer to the type of physical phenomena described by nonlinear optics [86]. Application of nonlinear optics to the study the migration of excitation energy in the photosynthetic unit led to the emergence of a new class of experimental data. Coherent monochromatic laser radiation allows selectively excitation of a desired portion of the spectral range, and using various signal detection schemes the population of excited levels change over time. Of course, these experimental conditions are far from what is called natural conditions; however, in certain settings you can get some idea of the physical and chemical processes of photosynthesis in plants and bacteria.

Modeling of nonlinear optical response is not a trivial task; it requires the calculation of the temporal evolution of the polarization of the object in interaction with the electromagnetic field. Like most quantum-mechanical problems, the exact solution for a system of interacting Chl molecules is impossible. One effective way to solve the problem is the use of techniques of projection operators [86]; it allows dividing the degrees of freedom into essential and nonessential, and thus receiving only the significant decision by approximating the contribution of the remaining degrees of freedom by the correlation functions. When modeling photosynthetic systems, excited electronic levels of chromatophores in the visible range are essential, and vibrational–rotational levels of pigment molecules and protein environment are not essential. In this case, the dynamics of the density matrix is given by the relaxation of the fourth-order tensor of the electronic excitations [87-92], and this method of calculation depends on the hierarchy of interactions in the system under study [93].

The model of localized excited states, which was formerly widely used to describe the energy transfer in photosynthesis, was no longer suitable for the whole class of experimental data. The hypothesis of energy transfer within light-harvesting complexes according the “hopping mechanism”, based on the assumption of incoherent Forster optical transitions between the molecules of pigment, was not working when trying to explain the abnormally high “bleaching” of chromatophores per one absorbed light quantum in pump-and-probe experiments.

The solution became possible after the assumption that current-free exciton states can be excited in the antennae of photosynthetic organisms [8, 66]. The exciton is a quantum quasi-particle and has no classical analog [69, 70]. Standard theory of excitons, which has been successfully applied in solid state physics, required some updates for calculations of the optical spectra and kinetic curves [91, 94-97]. Without going into detailed theoretical calculations, the idea of ​​the exciton can be illustrated by two interacting molecules. Assume that each of them has a ground and excited (not necessarily the same for different molecules, such as E_a and E_b) states, interaction energy V_ab, and dipole moments corresponding to the transition to these excited states. The Hamiltonian matrix of such a system has the form:

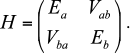
Then, the total energy E_± of the system consists of two levels

with the splitting equal to the so-called “Davydov splitting” [70]. The wave function of the system is the sum of products of molecular wave functions with appropriate weights. Thus, after light quantum absorption excitation is somewhat delocalized on two molecules and cannot be described only in an excited state of one of the molecules. Exciton states, in addition to the energy Eigen-values, ​​are characterized by moments of optically observed transitions, the values ​​of which do not coincide with the dipole moments of the individual molecules. However, the sum of the squares of exciton moments exactly equals the sum of the squares of the molecular dipole moments [86].

In real pigment–protein complexes the number of chromophores can reach several hundred. Exciton structure of such systems is entirely determined by the energy transition to the singlet excited state of the chromophore, the mutual arrangement of the chromophores, and the distances between them. Spectral values ​​of the energy of exciton excited states and their intensities may differ significantly from those for monomeric pigment molecules in solution, which is, typically, the evidence of exciton nature of energy transfer in the research object. One of the modern experimental methods of investigation is two-dimensional Fourier transform spectroscopy [98-100], which not only allows direct verification of the existence of excitons in the object of study, but also to determine the degree of coherence of the exciton states [101].

Energy of the pair interaction between molecules of pigments are usually calculated by most researchers in the dipole–dipole approximation. However, as shown specifically in theoretical studies [102, 103], in photosynthetic systems the use of the dipole–dipole approximation can lead to a tenfold overestimate the interaction energy between molecules. This occurs because for some molecules the size of the transition dipole moment to the singlet excited state is comparable (of the order of magnitude) to the intermolecular distance. This violates the conditions of applicability of the dipole–dipole approximation. The solution to this problem is possible by using the so-called extended dipole approximation [102], which provides a value of the interaction energy of the order comparable to exact DFT (density functional theory) methods [103], but with significant savings in computational resources.

Interaction with the vibrational degrees of freedom of the molecule, and with the nearest environment leads to the destruction of the coherent exciton states. Any system, regardless of the initial conditions, sooner or later reaches a state of thermodynamic equilibrium that is determined by the Boltzmann distribution. Therefore, to study the kinetics of the nonlinear optical response one needs to calculate the relaxation rates between exciton states [86].

The appearance of X-ray data for the crystals of light-harvesting complexes and reaction centers gave new life to theoretical studies of energy migration and charge separation. The ability to determine the arrangement of atoms of molecules with high accuracy showed a large enough range of intermolecular distances in antennas and, as a consequence, the simultaneous presence of weak and strong exciton interaction. As a result, the problem of modeling of femtosecond and picosecond kinetic curves of the exciton level populations was transformed into a well-formulated quantum-mechanical problem, which simply requires computer-engineering solutions.

Depending on the intensity of the exciton–exciton and exciton–vibronic interactions and magnitude of the interaction of excitons with the thermostat, the modern theoretical description includes four limiting cases, each of which we consider in detail below.

Weak dipole–dipole interaction between pigments and fast relaxation of electronic excitation due to the influence of the protein environment leads to localization of the excited state on the molecule. Energy transfer in this case is determined by the rate (proportional to R^–6), the orientation factor, and the square of the Coulomb interaction energy. This energy transfer is called incoherent energy transfer or Forster-type [31]. It is assumed that the excitation is completely on the donor or on the acceptor. The historical role of the Forster theory in the study of energy transfer in the antennae of light harvesting pigment–protein complexes was mentioned above.

Redfield theory is the most commonly used method for analyzing the dynamic properties of pigment–protein complexes in photosynthesis [94, 98, 104-106]. Initially, the mathematical apparatus of the theory was developed for the analysis of spin–spin and spin–lattice relaxation in metals and semiconductors [107], and only later it was adopted for the study of the exciton dynamics of molecular crystals. The main condition for the applicability of this theory is the presence of strong exciton–exciton and weak exciton–vibronic interaction, which leads to a Lorentzian line shape of individual delocalized exciton states [86, 107]. Energy migration implies successive relaxation to the low-energy levels of the system. Evaluation of relaxation rates is based on the spectral density function. However, the complex shape of the absorption spectra of chromatophores, which almost never corresponds to Lorentzian, imposes severe restrictions on the use of Redfield theory. It should be noted that at the moment there is no clearly defined criteria for the spectral density characterizing the exciton–vibronic interaction between the molecules of Chl and Bchl.

Attempts to overcome the contradictions led to the creation of the modified Redfield theory [88, 108]. The main postulate of the theory is that for strong exciton–exciton and exciton–vibronic interactions, the diagonal part of the Hamiltonian matrix of the system, describing the exciton–vibronic interaction, is regarded as an unperturbed quantum system. This method is used for calculating the rate of energy migration taking into account the contribution of vibrational states of molecules and, under certain conditions, it is much more precise than standard Redfield theory. Modified Redfield theory was applied to study energy transport in light-harvesting complexes of PS2 [36], PS1 [109], LHC-II trimers [110], as well as in the study of charge transport in RC isolated from PS2 [92, 106, 111]. An unpleasant artifact of the modified Redfield theory is its inability to take into account the dynamic localization of excitons. If the system has two weakly interacting isoenergetic levels, the calculation will show that they are strongly delocalized. In fact, this is not true, since in reality the exciton–vibronic interaction destroy the coherence of excitons, bringing the system to a complete localization of excited states. To resolve this problem, the unperturbed way off-diagonal elements of the exciton–vibronic Hamiltonian must be taken into account. In the method of hierarchical equations [112, 113], this disadvantage is eliminated, but instead we get a quantum system that requires very large computational resources.

It makes sense to consider in detail the ways of modeling the experimental data. Kinetic curves can contain up to tens of thousands of points in the time range and up to a hundred in the frequency range. Theoretical calculation of the nonlinear optical response of sophisticated light-harvesting complexes by simple parameter adjustment is usually ineffective because it is almost impossible to verify the uniqueness of the solution found. Most multiparameter optimization problems of this kind today are solved by methods of genetic algorithms (GA) [114, 115]. The main advantage of the GA is the ability to avoid the local minima of the characteristic function in the space of possible solutions. GA have their limitations, but they have already been successfully used in the study of RCs isolated from PS2 when searching for localized triplet states [90] and fitting of Stark spectra of excited levels, which characterize charge-separated states [92].

The method of differential evolution [114, 115] is a more effective method inherited from the GA idea. It allows searching for the infinite space of possible solutions. The search for a desired solution can be accelerated by selecting and configuring the algorithm for child parameter sets. The differential evolution method was used effectively in modeling the dynamics of charge-separated states in RCs of PS2 [111, 116] and for description of modulations of femtosecond kinetics obtained in the RCs of purple bacteria [117-119].

Despite the fact that X-ray analysis allowed literally looking inside the light-harvesting complexes and accurately determining the position of not only molecules, but also of individual atoms, the fundamental question of basic science – why photosynthesis is so efficient – remains unanswered. Nonlinear techniques permit registration of pico- and femtosecond lifetimes of exciton states and tracing of the migration of energy and charges. Almost immediately there appeared the problem of quantitative description and interpretation of experimental data. Schematic antenna models of the 1950-60s dictated by common sense and logic and having more to do with chemistry and biology than with physics were unable to explain the diversity of kinetic curves measured in optical laboratories of the late 1970s and early 1980s. However, not all the representations used in the “pre-laser era” are outdated. The theory of incoherent resonant Forster transfer, for example, is now considered as one of the possible approximations in the description of the dynamics of weakly interacting chromatophores. Modern exciton theory developed for the simulation of the optical response of biological systems under the influence of coherent radiation is also not universal. A large number of parameters that cannot be measured directly put more questions than answers. In particular, it remains a problem of coherent energy transport in vivo. In any case, further improvement of the measuring equipment and the development of methods for analyzing large amounts of experimental data of course far ahead advance the understanding of the nature of the primary processes of photosynthesis.

This work was partially supported by the Russian Foundation for Basic Research grant 12-02-31639-mol_a.

REFERENCES

1.Rabinowitch, E. (1959) Plant Physiol., 34, 213-218.
2.Rabinowitch, E. (1961) Physics-Uspekhy, 74, 289-302.
3.Borisov, A. Y. (1978) in The Photosynthetic Bacteria (Clayton, R. K., and Sistrom, W. R., eds.) Academic Press, New York, pp. 323-333.
4.Borisov, A. Y., Gadonas, R. A., Danielius, R. V., Piskarskas, A. S., and Razjivin, A. P. (1982) FEBS Lett., 138, 25-28.
5.Razjivin, A. P., Danielius, R. V., Gadonas, R. A., Borisov, A. Y., and Piskarskas, A. S. (1982) FEBS Lett., 143, 40-44.
6.Abdourakhmanov, I. A., Danielius, R. V., and Razjivin, A. P. (1989) FEBS Lett., 245, 47-50.
7.Danielius, R. V., Mineyev, A. P., and Razjivin, A. P. (1989) FEBS Lett., 250, 183-186.
8.Novoderezhkin, V. I., and Razjivin, A. P. (1993) FEBS Lett., 330, 5-7.
9.Novoderezhkin, V. I., and Razjivin, A. P. (1994) Photosynth. Res., 42, 9-15.
10.Novoderezhkin, V. I., and Razjivin, A. P. (1995) Biophys. J., 68, 1089-1100.
11.McDermott, G., Prince, S. M., Freer, A. A., Hawthornthwaite-Lawless, A. M., Papiz, M. Z., Cogdell, R. J., and Isaacs, N. W. (1995) Nature, 374, 517-521.
12.Koepke, J., Hu, X. C., Muenke, C., Schulten, K., and Michel, H. (1996) Structure, 4, 581-597.
13.Dracheva, T. V., Novoderezhkin, V. I., and Razjivin, A. P. (1996) FEBS Lett., 387, 81-84.
14.Alden, R. G., Johnson, E., Nagarajan, V., and Parson, W. W. (1997) J. Phys. Chem. B, 101, 4667-4680.
15.Cogdell, R. J., Isaacs, N. W., Freer, A. A., Arrelano, J., Howard, T. D., Papiz, M. Z., Hawthornthwaite-Lawless, A. M., and Prince, S. (1997) Prog. Biophys. Mol. Biol., 68, 1-27.
16.Novoderezhkin, V., Monshouwer, R., and van Grondelle, R. (1999) J. Phys. Chem. B, 103, 10540-10548.
17.Bakalis, L. D., Coca, M., and Knoester, J. (1999) J. Chem. Phys., 110, 2208-2218.
18.Sundstrom, V., Pullerits, T., and van Grondelle, R. (1999) J. Phys. Chem. B, 103, 2327-2346.
19.Brown, A. H., and Frenkel, A. W. (1953) Annu. Rev. Plant Physiol. Plant Mol. Biol., 4, 23-58.
20.Calvin, M., Bassham, J. A., Benson, A. A., and Massini, P. (1952) Annu. Rev. Phys. Chem., 3, 215-228.
21.Lumry, R., Spikes, J. D., and Eyring, H. (1953) Annu. Rev. Phys. Chem., 4, 399-424.
22.Rabinowitch, E. (1952) Annu. Rev. Plant Physiol. Plant Mol. Biol., 3, 229-264.
23.Emerson, R., and Arnold, W. (1932) J. Gen. Physiol., 16, 191-205.
24.Emerson, R., and Arnold, W. (1932) J. Gen. Physiol., 15, 391-420.
25.Gaffron, H., and Wohl, K. (1936) Naturwissenschaften, 24, 103-107.
26.Gaffron, H. (1936) Biochemische Zeitschrift, 287, 130-139.
27.Rabinowitch, E. (1945) Photosynthesis and Related Processes. Chemistry of Photosynthesis, Chemosynthesis and Related Processes in vitro and in vivo, Interscience Publishers Inc., New York, http://www.life.illinois.edu/govindjee/Electronic Publications/Books.
28.Hodge, A. J., McLean, J. D., and Mercer, F. V. (1955) J. Biophys. Biochem. Cytol., 1, 605-614.
29.Jacobs, E. E., Holt, A. S., Kromhout, R., and Rabinowitch, E. (1957) Arch. Biochem. Biophys., 72, 495-511.
30.Wolken, J. J., and Schwertz, F. A. (1953) J. Gen. Physiol., 37, 111-120.
31.Forster, T. (1948) Annalen der Physik, 2, 55-75.
32.Novoderezhkin, V. I., and Razjivin, A. P. (1993) FEBS Lett., 330, 5-7.
33.Dracheva, T. V., Novoderezhkin, V. I., and Razjivin, A. P. (1995) Chem. Phys., 194, 223-235.
34.Novoderezhkin, V. I., and Razjivin, A. P. (1995) Photosynthetica, 31, 147-151.
35.Dracheva, T. V., Novoderezhkin, V. I., and Razjivin, A. P. (1996) FEBS Lett., 387, 81-84.
36.Raszewski, G., and Renger, T. (2008) J. Am. Chem. Soc., 130, 4431-4446.
37.Goedheer, J. C. (1955) Biochim. Biophys. Acta, 16, 471-476.
38.Goedheer, J. C. (1955) Nature, 176, 928-929.
39.Krasnovsky, A. A. (1960) Annu. Rev. Plant Physiol., 11, 363-410.
40.Krasnovsky, A. A. (1965) Photochem. Photobiol., 4, 641-655.
41.Krasnovsky, A. A., and Bystrova, M. I. (1980) Biosystems, 12, 181-194.
42.Krasnovsky, A. A., and Brin, G. P. (1948) Doklady AN SSSR, 63, 163-166.
43.Krasnovsky, A. A., and Kosobutskaya, L. M. (1953) Doklady AN SSSR, 91, 343-346.
44.Krasnovsky, A. A., Kosobutskaya, L. M., and Voinovskaya, K. K. (1953) Doklady AN SSSR, 92, 1201-1204.
45.Albers, V. M., and Knorr, H. V. (1937) Plant Physiol., 12, 833-843.
46.Brugger, J. E., and Franck, J. (1958) Arch. Biochem. Biophys., 75, 465-496.
47.Franck, J. (1958) Proc. Natl. Acad. Sci. USA, 44, 941-948.
48.Brody, S. S., and Brody, M. (1961) Biochim. Biophys. Acta, 54, 495-505.
49.Duysens, L. N. M. (1956) Annu. Rev. Plant Physiol. Plant Mol. Biol., 7, 25-50.
50.Wohl, K. (1937) Zeitschrift fur Physikalische Chemie-Abteilung B-Chemie der Elementarprozesse Aufbau der Materie, 37, 209-230.
51.Duysens, L. N. M. (1952) Transfer of Excitation Energy in Photosynthesis, Thesis, Utrecht, pp. 1-96.
52.Duysens, L. N. M., Huiskamp, W. J., Vos, J. J., and Vanderhart, J. M. (1956) Biochim. Biophys. Acta, 19, 188-190.
53.Franck, J., and Teller, E. (1938) J. Chem. Phys., 6, 861-872.
54.Brody, S. S., and Rabinowitch, E. (1957) Science, 125, 555-557.
55.Zankel, K. L., Reed, D. W., and Clayton, R. K. (1968) Proc. Natl. Acad. Sci. USA, 61, 1243-1249.
56.Reed, D. W., and Clayton, R. K. (1968) Biophys. J., 8, Suppl. 1, A150.
57.Reed, D. W., and Clayton, R. K. (1968) Biochem. Biophys. Res. Commun., 30, 471-475.
58.Martin, J. L., Breton, J., Hoff, A. J., Migus, A., and Antonetti, A. (1986) Proc. Natl. Acad. Sci. USA, 83, 957-961.
59.Shelaev, I. V., Gostev, F. E., Mamedov, M. D., Sarkisov, O. M., Nadtochenko, V. A., Shuvalov, V. A., and Semenov, A. Y. (2010) Biochim. Biophys. Acta - Bioenergetics, 1797, 1410-1420.
60.Spitzer, F. (1969) Principles of Random Walk [Russian translation], Mir, Moscow.
61.Zankel, K. L., and Clayton, R. K. (1968) Biophys. J., 8, Suppl. 1, A151.
62.Bergstrom, H., Westerhuis, W. H. J., Sundstrom, V., Vangrondelle, R., Niederman, R. A., and Gillbro, T. (1988) FEBS Lett., 233, 12-16.
63.Timpmann, K., Zhang, F. G., Freiberg, A., and Sundstrom, V. (1993) Biochim. Biophys. Acta, 1183, 185-193.
64.Nuijs, J. T. M., Aartsma, T. J., and Amesz, J. (1994) Biochim. Biophys. Acta, 1188, 278-286.
65.Valkunas, L., Razjivin, A., and Trinkunas, G. (1985) Photobiochem. Photobiophys., 9, 139-142.
66.Novoderezhkin, V. I., and Razjivin, A. P. (1995) Biophys. J., 68, 1089-1100.
67.Razjivin, A. P., Leupold, D., and Novoderezhkin, V. I. (1998) in Photosynthesis: Mechanisms and Effects, Vol. 1 (Garab, G., ed.) Kluwer Academic Publishers, Dorderecht, The Netherlands, pp. 15-20.
68.Agranovich, V. M. (2008) Excitations in Organic Solids, Oxford University Press Inc., New York.
69.Knox, R. S. (1963) Theory of Excitons, Academic Press, New-York-London.
70.Davydov, A. S. (1971) Theory of Molecular Excitons, Plenum Press, New York.
71.Novoderezhkin, V. I., and Razjivin, A. P. (1995) Photochem. Photobiol., 62, 1035-1040.
72.Roszak, A. W., Howard, T. D., Southall, J., Gardiner, A. T., Law, C. J., Isaacs, N. W., and Cogdell, R. J. (2003) Science, 302, 1969-1972.
73.Noy, D. (2008) Photosynth. Res., 95, 23-35.
74.Strumpfer, J., Sener, M., and Schulten, K. (2012) J. Phys. Chem. Lett., 3, 536-542.
75.Dorfman, K. E., Voronine, D. V., Mukamel, S., and Scully, M. O. (2013) Proc. Natl. Acad. Sci. USA, 110, 2746-2751.
76.Kominis, I. K. (2013) New J. Phys., 15, 075017.
77.Manzano, D. (2013) Plos One, 8, e57041.
78.Reimers, J. R., Cai, Z. L., Kobayashi, R., Ratsep, M., Freiberg, A., and Krausz, E. (2013) Sci. Rep., 3, 2761-2768.
79.Kohler, J., van Oijen, A. M., Ketelaars, M., Hofmann, C., Matsushita, M., Aartsma, T. J., and Schmidt, J. (2001) Int. J. Modern Phys. B, 15, 3633-3636.
80.Matsushita, M., Ketelaars, M., van Oijen, A. M., Kohler, J., Aartsma, T. J., and Schmidt, J. (2001) Biophys. J., 80, 1604-1614.
81.Ketelaars, M., van Oijen, A. M., Matsushita, M., Kohler, J., Schmidt, J., and Aartsma, T. J. (2001) Biophys. J., 80, 1591-1603.
82.Van Oijen, A. M., Ketelaars, M., Matsushita, M., Kohler, J., Aartsma, T. J., and Schmidt, J. (2001) Biophys. J., 80, 151A.
83.Engel, G. S., Calhoun, T. R., Read, E. L., Ahn, T. K., Mancal, T., Cheng, Y. C., Blankenship, R. E., and Fleming, G. R. (2007) Nature, 446, 782-786.
84.Collini, E., Wong, C. Y., Wilk, K. E., Curmi, P. M. G., Brumer, P., and Scholes, G. D. (2010) Nature, 463, 644-647.
85.Engel, G. S., Calhoun, T. R., Read, E. L., Ahn, T. K., Mancal, T., Cheng, Y. C., Blankenship, R. E., and Fleming, G. R. (2007) Nature, 446, 782-786.
86.Mukamel, S. (1995) Principles of Nonlinear Optical Spectroscopy, Oxford University Press.
87.Kuhn, O., Renger, T., May, V., Voigt, J., Pullerits, T., and Sundstrom, V. (1997) Trends Photochem. Photobiol., 4, 213-255.
88.Meier, T., Chernyak, V., and Mukamel, S. (1997) J. Chem. Phys., 107, 8759-8780.
89.Renger, T., and May, V. (1997) Phys. Rev. Lett., 78, 3406-3409.
90.Raszewski, G., Saenger, W., and Renger, T. (2005) Biophys. J., 88, 986-998.
91.Van Grondelle, R., and Novoderezhkin, V. I. (2006) Phys. Chem. Chem. Phys., 8, 793-807.
92.Novoderezhkin, V. I., Dekker, J. P., and van Grondelle, R. (2007) Biophys. J., 93, 1293-1311.
93.Yang, M. N., and Fleming, G. R. (2002) Chem. Phys., 275, 355-372.
94.Renger, T., May, V., and Kuhn, O. (2001) Phys. Rep. – Rev. Sec. Phys. Lett., 343, 138-254.
95.Mukamel, S., and Abramavicius, D. (2004) Chem. Rev., 104, 2073-2098.
96.Renger, T. (2009) Photosynth. Res., 102, 471-485.
97.Van Grondelle, R., and Novoderezhkin, V. I. (2010) Nature, 463, 614-615.
98.Brixner, T., Stenger, J., Vaswani, H. M., Cho, M., Blankenship, R. E., and Fleming, G. R. (2005) Nature, 434, 625-628.
99.Mancal, T., Pisliakov, A. V., and Fleming, G. R. (2006) J. Chem. Phys., 124, 234504.
100.Pisliakov, A. V., Mancal, T., and Fleming, G. R. (2006) J. Chem. Phys., 124, 234505.
101.Lewis, K. L. M., Fuller, F. D., Myers, J. A., Yocum, C. F., Mukamel, S., Abramavicius, D., and Ogilvie, J. P. (2013) J. Phys. Chem. A, 117, 34-41.
102.Nagamura, T., and Kamata, S. (1990) J. Photochem. Photobiol. A-Chem., 55, 187-196.
103.Madjet, M. E., Abdurahman, A., and Renger, T. (2006) J. Phys. Chem. B, 110, 17268-17281.
104.Renger, T., and Marcus, R. A. (2002) J. Chem. Phys., 116, 9997-10019.
105.Novoderezhkin, V. I., Yakovlev, A. G., van Grondelle, R., and Shuvalov, V. A. (2004) J. Phys. Chem. B, 108, 7445-7457.
106.Novoderezhkin, V. I., Andrizhiyevskaya, E. G., Dekker, J. P., and van Grondelle, R. (2005) Biophys. J., 89, 1464-1481.
107.Redfield, A. G. (1965) in Advances in Magnetic Resonance (Waugh, J. S., ed.) Academic Press, New York-London, pp. 1-32.
108.Zhang, W. M., Meier, T., Chernyak, V., and Mukamel, S. (1998) J. Chem. Phys., 108, 7763-7774.
109.Yang, M., Damjanovic, A., Vaswani, H. M., and Fleming, G. R. (2003) Biophys. J., 85, 140-158.
110.Novoderezhkin, V. I., and van Grondelle, R. (2010) Phys. Chem. Chem. Phys., 12, 7352-7365.
111.Pishchalnikov, R., Mueller, M., and Holzwarth, A. (2007) Photosynth. Res., 91, 141.
112.Ishizaki, A., and Fleming, G. R. (2009) Proc. Natl. Acad. Sci. USA, 106, 17255-17260.
113.Ishizaki, A., and Fleming, G. R. (2009) J. Chem. Phys., 130, 234110.
114.Storn, R., and Price, K. (1997) J. Global Optimization, 11, 341-359.
115.Storn, R. (1999) IEEE Trans. Evol. Comput., 3, 22-34.
116.Pishchalnikov, R. Y., Muller, M. G., and Holzwarth, A. R. (2008) in Photosynthesis. Energy from the Sun (Allen, J. F., Gantt, E., Golbeck, J. H., and Osmond, B., eds.) Springer, pp. 163-166.
117.Pershin, S. M., and Pishchalnikov, R. Y. (2012) Physics of Wave Phenomena, 20, 35-44.
118.Pishchalnikov, R. Y., Pershin, S. M., and Bunkin, A. F. (2012) Physics of Wave Phenomena, 20, 184-192.
119.Pishchalnikov, R. Y., Pershin, S. M., and Bunkin, A. F. (2012) Biophysics, 57, 779-785.

---