Mechanisms of Generation of Local ΔpH in Mitochondria and Bacteria
E. S. Medvedev1* and A. A. Stuchebrukhov2
1Institute of Problems of Chemical Physics, Russian Academy of Sciences, pr. Akademika Semenova 1, 142432 Chernogolovka, Moscow Region, Russia; fax: (496) 522-3507; E-mail: esmedved@orc.ru2Department of Chemistry, University of California, Davis, CA 95616, USA; fax: (530) 752-8995; E-mail: stuchebr@chem.ucdavis.edu
* To whom correspondence should be addressed.
Received November 24, 2013; Revision received February 8, 2014
The concepts of global and local coupling between proton generators, the enzymes of the respiratory chain, and the consumer, the ATP synthase, coexist in the theory of oxidative phosphorylation. Global coupling is trivial proton transport via the aqueous medium, whereas local coupling implies that the protons pumped are consumed before they escape to the bulk phase. In this work, the conditions for the occurrence of local coupling are explored. It is supposed that the membrane retains protons near its surface and that the proton current generated by the proton pumps rapidly decreases with increasing proton motive force (pmf). It is shown that the competition between the processes of proton translocation across the membrane and their dissipation from the surface to the bulk can result in transient generation of a local ΔpH in reply to a sharp change in pmf; the appearance of local ΔpH, in turn, leads to rapid recovery of the pmf, and hence, it provides for stabilization of the potential at the membrane. Two mechanisms of such kind are discussed: 1) pH changes in the surface area due to proton pumping develop faster than those due to proton escape to the bulk; 2) the former does not take place, but the protons leaving the surface do not equilibrate with the bulk immediately; rather, they give rise to a non-equilibrium concentration near the surface and, as a result, to a back proton flow to the surface. The first mechanism is more efficient, but it does not occur in mitochondria and neutrophilic bacteria, whereas the second can produce ΔpH on the order of unity. In the absence of proton retardation at the surface, local ΔpH does not arise, whereas the formation of global ΔpH is possible only at buffer concentration of less than 10 mM. The role of the mechanisms proposed in transitions between States 3 and 4 of the respiratory chain is discussed. The main conclusion is that surface protons, under conditions where they play a role, support stabilization of the membrane pmf and rapid communication between proton generators and consumers, while their contribution to the energetics is not significant.
KEY WORDS: ATP synthesis, proton motive force, proton pump, local coupling, global couplingDOI: 10.1134/S000629791405006X
Abbreviations: B, bacterial membrane; CP, chemical potential gradient at the membrane; EP, electric potential gradient at the membrane; M, mitochondrial membrane; pmf, proton motive force; δpHa, local pH change with respect to the equilibrium value at a given side of the membrane (see Eq. (19)); ΔpHa, local transmembrane pH gradient (see Eq. (20)).
The reaction of ATP synthesis obeys the general thermodynamic relation
between the rate constants for the forward and backward reactions: the
ratio of these constants, i.e. the equilibrium constant depends only on
the difference of the electrochemical potentials between two sides of
the membrane Δμ̃H+, or proton
motive force Δμ̃H+/F
(pmf),
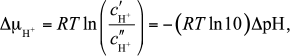 (2)
(2)and is independent of its individual components, the gradients of the electrical Δφ = φ′ – φ′′ and chemical ΔμH+ potentials (EP and CP). However, each of the two rates can differently depend on the pmf components, which manifests under non-equilibrium conditions created by the work of the proton pumps. The question of the actual form of this dependence is still debated: some authors believe that there is no such dependence [1, 2], and others suggest that there is a dependence upon pH [3]. Here we consider the problem of generation of Δφ and ΔpH by proton pumps; both mitochondria and neutrophilic bacteria will be considered.
The issue of Δφ generation is resolved simply. Let the membrane capacitance per unit area and its surface area be Cmemb and Smemb, respectively. Then, translocation of one elementary charge e0 across the membrane produces the potential gradient φe = e0/(Cmemb Smemb). For the mitochondrial (M) and bacterial (B) membranes with parameters from Table 1, one gets φe = 0.25 and 20 µV, respectively.
Table 1. The model parameters
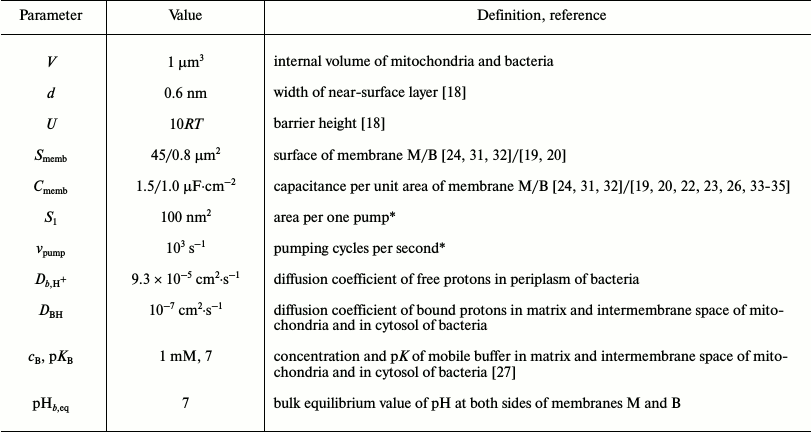
* In [16], the values of
S1 = 500 nm2 and
vpump = 500 s–1 are used.
The issue of ΔpH generation is more complicated. In mitochondria, the matrix and intermembrane space contain highly concentrated buffers that oppose any pH change. The bacterial cytosol also contains large concentrations of buffers, while the periplasm communicates with the outer medium of practically infinite volume. Williams [4-7] proposed the concept of local coupling in the theory of oxidative phosphorylation, which assumed generation of local ΔpH inside the membrane or, by Kell’s version [8], at its surface, in contrast to the global ΔpH in Mitchell’s theory [9]. Many data have been accumulated in the literature to support the local mechanism [10, 15] (see also [16, 17] and references therein). The possibility of generation of local pH changes at biological membranes has been considered theoretically [16]. However, to the best of our knowledge, no theoretical foundation has been presented for the possibility of local ΔpH generation at the membranes in buffered media.
In this paper, we suggest a formula to describe the dependence of the proton pump current on the membrane pmf and on the system parameters. Based on this formula and our kinetic theory of diffusion of protons near membranes [18], we propose two mechanisms of generation of local ΔpH.
Concerning the membrane, it is assumed that near the membrane surface there exists some region a, two H bonds wide, in which the protons are attracted to the membrane; in region a, proton concentration is significantly increased with respect to the bulk region b due to attraction of the protons by the membrane. The local pH changes with respect to their equilibrium values (denoted as δpHa) arise within regions a at both sides of the membrane. The local ΔpH generation mechanisms are as follows.
1. Due to a high density of the proton pumping enzymes on the membrane and a small volume of the near-membrane attractive region a, the rate of changes in proton concentration in this region caused by the proton pumps can be extremely high at low pmf, on the order of the rate of proton exchange between a and b. In such case, δpHa increases up to the maximum level defined by the competition between the two outlined processes.
2. Even if the pumping rate is not sufficiently high so that mechanism 1 does not work, generation of δpHa is still possible owing to slow proton diffusion away from the surface. As shown in our previous work [18], fast exchange of the non-equilibrium protons between regions a and b, as compared to their diffusion, results in slow depletion kinetics of protons from the surface region a; the depletion occurs by a very slow power law, which can lead to a buildup of δpHa.
Mechanisms 1 and 2 can result in significant, though transient, changes in local pH in the regions near the surface upon sharp changes in pmf; however, this occurs only on the condition that the concentration of the mobile buffer does not exceed 1 mM. In the absence of the surface effect, changes in the global pH are small (<0.1) in the presence of high buffer concentrations ~100 mM, and they are significant at concentrations less than 10 mM. More significant pH changes in the bulk arise with the inclusion of transport of other cations [19, 20].
The predicted mechanisms can be explored by the methods of fluorescence correlation spectroscopy [21], which allow for measurements of the kinetics of the protonation processes on biological membranes in the time range from picoseconds to seconds.
In the section “Proton Pump Model” below, a model of the proton pump is introduced that assumes that the pumping rate depends only on pmf and decreases exponentially with increasing pmf. The calculations showed that the pump stops working when pmf reaches a limiting value close to the physiological value of 200 mV. This result was obtained without any adjustment of the parameters, which assures the validity of the model. The limiting pmf value mainly depends on the temperature and the pump parameters and weakly on the composition of the solution and the properties of the membrane.
The section “Physical Mechanisms of Generation of Local ΔpH and Conditions for Their Realization” describes mechanisms 1 and 2 and the conditions for their realization. The calculated kinetics of generation of the pmf and the local pH changes are shown in the section “Results of the Calculations”. In the last section, an application of the results to the description of transitions between States 3 and 4 of the respiratory chain [22, 23] is discussed.
PROTON PUMP MODEL
Let the membrane area Smemb host Npump = Smemb/S1 pumps, which occupy area S1 per pump and translocate zpump units of positive charge per cycle. For instance, cytochrome c oxidase uptakes, in one cycle, four protons from the negative (N) side of the membrane and four electrons from the positive (P) side to encounter at the catalytic center in the middle of the membrane, which is equivalent to the transfer of four positive charges across the whole membrane (“chemical” charges), and four other protons are pumped; thus, zpump = 8 Npump. Assume that the pump makes νpump cycles per second. In our model, the proton current, i.e. the number of protons taken up at the N side by all pumps across 1 cm2 of the membrane in 1 s is given by the formula:
where
is a time constant determining the maximum pump rate at zero pmf. When the pumps are turned on at moment t = 0, the current is maximal since Δμ̃H+ = 0, and it rapidly decreases at t > 0 because of generation of Δμ̃H+ < 0.
In Eq. (3), the exponential factor restricts the pmf buildup by the thermodynamic limit, i.e. by the maximal value that can be reached under continuous pumping in the absence of consumers. The maximal pumping rate, i.e. the rate at pmf = 0 given by the prefactor, is proportional to the number of pumps on the membrane, Npump, and therefore is very large, much larger than the turnover rate of a single pump, νpump. However, the maximal current exists only very transiently because the pmf rapidly increases and the current decreases.
To justify formula (3), we calculated the kinetics of generation of Δμ̃H+ across the organelle membrane, both for mitochondria and bacteria, and the current through the pumps under condition of equilibrium between the surface and the bulk, i.e. when the local ΔpH was absent. It was assumed that the initial conditions at t = 0 were identical on both sides of the membrane and that at t > 0 the constant values of φ′′ = 0 and pH′′ are maintained at the P side. The calculations were performed at pH′′ 6, 7, and 8, with and without buffer with pKB = 7 and concentration cB = 100 mM; in the latter case ions were added: potassium, sodium, and chlorine for bacteria (0.005, 4, and 3.955 M at pH 7, respectively), as in [19, 20], and 0.15 M potassium and chlorine each for mitochondria, as in [24]. The membrane and pump parameters are given in Table 1.
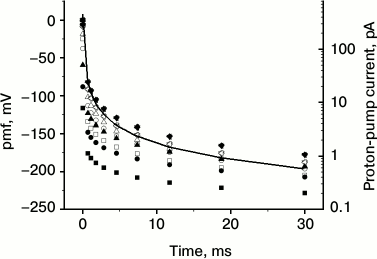
The results of the calculations are shown in Fig. 1. They demonstrate the basic features of the proposed model. First, all kinetic curves run within a physiologically acceptable range of pmf values despite strong variations of the composition and acidity of the solution, as well as a large difference in the number of pumps (50-fold) in the two membranes. This suggests that the model is reasonable. The data of Fig. 1 are interesting in view of developing precision methods to measure currents across cytoplasmic membranes and the local ΔpH on them [25]. The currents across the oocyte plasma membrane measured in [25] are 100-300 nA, and the local ΔpH is 0.1-0.3 with accuracy of 0.005. The calculated electric current jpump = e0Jpump in our Fig. 1 is three orders of magnitude smaller, which is associated with the smaller dimension of mitochondria.
Fig. 1. Kinetics of pmf generation (points, left ordinate) by the proton pumps at bacterial (filled symbols) and mitochondrial (empty symbols) membranes at pH 6, 7, and 8 with 100 mM buffer and without it (symbols of various shapes), and the proton-pump current in mitochondrial membrane with buffer at pH 7 (line, right ordinate). See Table 1 for the model parameters. Calculations were performed using formula (3).
Second, when the pumps turn on, an instantaneous jump of the pmf takes place, so that the absolute pmf value reaches RT/F = 25 mV during 50 to 0.1 µs for the curves in Fig. 1, and thereafter the increase in pmf slows significantly. The ultimate stabilization occurs much later when consumers and leaks come into effect (see “Discussion” section). If τss stands for the time to reach the steady state and τpmf for the characteristic time for pmf to increase to –25 mV (the estimates of τpmf are given above), then the limiting value of the pmf is of the order of magnitude:
It is proportional to temperature and depends logarithmically on the system parameters determining the initial rate of the pmf change. For the curves in Fig. 1 and τss = 30 ms, the value of Eq. (5) varies between –160 and –320 mV, which is roughly consistent with the values from –180 to –230 mV in Fig. 1.
The main advantage of the present model is that it describes the kinetics of pmf generation qualitatively correctly; its major consequence is that the rate of pmf increase at zero pmf is extremely high.
At the same time, formula (3) predicts a rapid slowing of the pump with increasing pmf, beginning with zero pmf, which seems to be unjustified. It is more reasonable to assume that the pump should slow sharply only when pmf reaches some critical value, say, –150 mV. To take this into account, we replace Eq. (3) with the following formula:
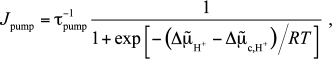 (6)
(6)where the critical value is taken to be Δμ̃c,H+ = –6RT; as a result, the decrease in the current with increasing the pmf slows (see Fig. S1 in the Supplement to the paper on the website of Biochemistry (Moscow) (http://protein.bio.msu.ru/biokhimiya)). Such a replacement does not affect the behavior of the kinetic curves qualitatively (see Fig. S2 in the Supplement), but it results in that the physiological (“locking”) pmf is reached much more rapidly (cf. Fig. 1 and Fig. S2, where the time scale is changed by a factor of 10), and hence the local pH changes will be larger at a given relaxation rate of non-equilibrium protons. Variations of Δμ̃c,H+ will result only in changes in the time to reach the locking pmf at which the current drops significantly. The role of this parameter will be discussed in the “Discussion” section.
Drachev et al. [19, 20] postulated a model in which, when pumps are switched on, the pmf immediately jumps up to a “working” value and then smoothly varies when the consumers come into play and the slow processes of potassium and sodium exchange begin. In contrast, we are considering the fast process of the pmf buildup, for it is during this process the possibility arises to create a local ΔpH at the membrane. In the following sections we will show how this occurs and what ΔpH can be obtained.
PHYSICAL MECHANISMS OF GENERATION OF LOCAL ΔpH AND
CONDITIONS FOR THEIR REALIZATION
Numerous experiments have established that protons can travel along artificial and natural biological membranes over macroscopically long distances, up to hundreds of microns (see review [17]), which corresponds to an apparent proton retention time at the surface of the order of 1 s. On the other hand, estimates of the actual retention time show that the time for spontaneous proton detachment, koff,sp–1 is quite short (see [18] and Table 2). To explain this phenomenon, we proposed a model according to which attraction of the dissociated protons by the negatively charged surface and quasi-one-dimensional type of their diffusion away from the surface lead to frequent returns of the protons from the bulk; as a result, the protons diffuse along the surface by making excursions to the bulk and back (see [18] and references therein). This model does not apply to mitochondria and bacteria directly, where no space is available for long proton translocations because of small dimensions of the membranes and high density of their coverage by enzymes [26]. Yet membrane attraction can locally affect the concentration of free protons and the kinetics of its changes.
Table 2. Calculated parameters

Let the attraction create a potential well of depth U and width d (region a) near the membrane surface. The equilibrium constant between a and the adjacent region b is expressed by the formula [18]:
The equilibrium concentrations in a and b are related by:
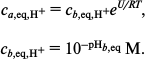 (8)
(8)The parameter estimates are given in [18]: d = 0.6 nm and U = (5-16)RT. The presence of the barrier results in a local decrease in the equilibrium pHa,eq with respect to bulk pHb,eq, but we will assume that this decrease is the same at both sides of the membrane and hence does not contribute to the difference ΔpHa = pHa′ – pHa′′, which is created only by the pumping and is determined by the competition between the proton pumping and the proton exchange with region b.
The total rate of proton escape from a to b is expressed by the formula1
which accounts for both the spontaneous detachment of the protons and their escape due to collisional transfer to the deprotonated buffer B– (it is assumed that buffer does not penetrate to a). The constant ka,off,B– is proportional to the mobile buffer concentration cB, which is much smaller than the total concentration estimated in the limits of 10-100 mM [20, 24]; for calculations, we take cB = 1 mM [27]. The estimates of the constants are given in the Supplement and Table 2; for a barrier height U = 10RT, the value of koff,sp–1 = 0.1 µs is obtained. This should be compared with the maximal rate of the pH change, which is reached (just as the rate of the pmf change) at small pmf values. The rate of the pH change depends not only on the pumping rate, but also on the pH value and the amount of buffer. If it is comparable with the rate of escape from a to b, then the local ΔpHa will be generated (mechanism 1).
1 Here and below, for the sake of argument, we are talking about the P side, the full description being given in the Supplement. In particular, the back flow from b to a is given by (S36) of the Supplement. If, on the contrary, the protons escape from a to b faster than they are pumped, mechanism 1 does not work, and then one has to consider what happens with the protons in region b itself. As protons are transferred from a to b, in region b adjacent to a non-equilibrium proton concentration builds up; it dissipates with time due to diffusion, but this is a slow process as compared to pumping. The estimates show (see Supplement and Table 2) that the characteristic time of this process, t0 (see definition in (S21) and (S16) of the Supplement), is long compared to the time for detachment from the surface (the so-called regime of fast surface–bulk exchange [17, 28-30]):
In the presence of the buffer, the non-equilibrium protons are in the bound state, BH, while in the absence of the buffer they are “free” protons2, H+; in both cases, however, the overall picture is the same. Owing to (10), i.e. due to slow diffusion of the protons (free or bound) in the direction away from the surface, the non-equilibrium protons accumulate near the surface and create the back flow to the surface, which delays the equilibration between the surface and the bulk. As a result, local ΔpH is generated (mechanism 2).
2 In fact, they are associated with water molecules in the form of hydronium ions, but this is of no importance in the present context. Let us formulate the quantitative conditions for the efficient generation of local ΔpHa. The proton pumping creates both ΔpHa and Δψ = FΔφ/RT, and it stops upon reaching the limiting pmf. Therefore, it is necessary that the characteristic time for the ΔpHa buildup is smaller than the time for the Δψ buildup:
Formulae for both characteristic times are derived in the Supplement (see (S66) and (S69)):
where
is equilibrium proton number in region a, Va = Smemb d, NA is Avogadro number, and
is the dimensionless potential gradient arising at the membrane on the transfer of a single proton (see (S68) in the Supplement). According to the reasoning presented above, mechanisms 1 and 2 are realized under the conditions
and
respectively. Formulae for calculations of ka,off and t0 are given in the Supplement (see (S1)-(S7), (S20), and (S21)).
RESULTS OF CALCULATIONS
To examine the time dependence of the membrane potentials and pmf, it is necessary to solve a system of coupled kinetic equations describing the evolution of EP and CP at both sides of the membrane as well as the proton distribution in the bulk near the surface. We will assume that the membrane is charging from zero potential, and we are interested in how the pmf is reaching its maximum value. One can also say that we consider the response function of the membrane to a sharp or sudden change in the state of the system when the pmf drops to zero, and we want to examine how the pmf is restoring to its steady-state value.
The mathematical formulation of the problem and its solution are given in the Supplement. The results of the calculations with the parameters from Tables 1 and 2 are given in Fig. 2 for mitochondrial membrane M and in Fig. 3 for bacterial membrane B. As seen from Table 2, for the selected parameters (Table 1), conditions (10) and (11) are fulfilled, whereas the left inequality (16) is not, i.e. mechanism 1 does not work; this is because of the insufficiently fast change in pHa. As follows from Eq. (12), one can accelerate this process, i.e. decrease τa,pH, by lowering the equilibrium proton concentration in region a. This can be achieved by increasing pHb,eq by 2 units and more. Investigation of alkaliphiles is beyond the scope of the present paper because, for them, one probably has to change the pump formulae (3) and (6). Lowering the barrier will give no effect since ka,off–1 will shorten simultaneously with τa,pH and proportionally to it.
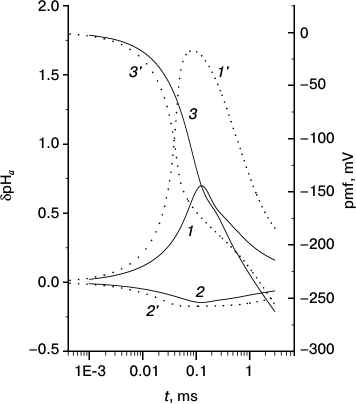
Fig. 2. Kinetics of generation of local pH changes at the internal (1, 1′) and external (2, 2′) sides of a mitochondrial membrane and proton motive force (3, 3′) at two concentrations of the mobile buffer: 1 mM (solid lines 1-3) and 0.5 mM (dotted lines 1′-3′).
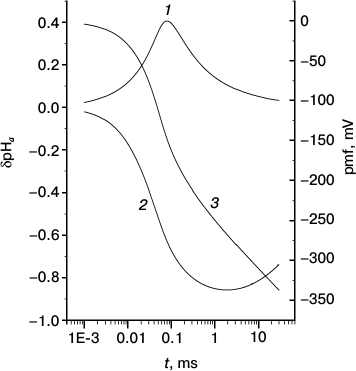
Fig. 3. Kinetics of generation of local pH changes at the internal (1) and external (2) sides of a bacterial membrane and proton motive force (3).
Condition (17) for realization of mechanism 2 is fulfilled only partly: the left inequality is obeyed in all cases, whereas the right one is valid only at the P side of membrane B, i.e. in the absence of buffer, when the solution contains only free protons and t0 is long enough (while the free protons diffuse much faster than the bound ones, they have to cover much longer distance L0,H+ to escape to the bulk (see (S16) in the Supplement)). We note, however, that breaking the right inequality (17) does not mean that mechanism 2 is disabled completely. As a matter of fact, proton dissipation to the bulk proceeds extremely slowly by the power law [18]:
where pa(t) is the fraction of the pumped protons remaining in region a at moment t. Even at t > t0, region a still contains a sufficiently large number of protons because of the power-law decay. For example, for t0 = 0.7 µs, at t = τa,pH = 10 µs, in region a there still remains some 13% of the non-equilibrium protons, which can result in appreciable changes of pHa due to the small volume of region a. This is demonstrated by the results shown in Figs. 2-4, which are discussed in the “Discussion” section.
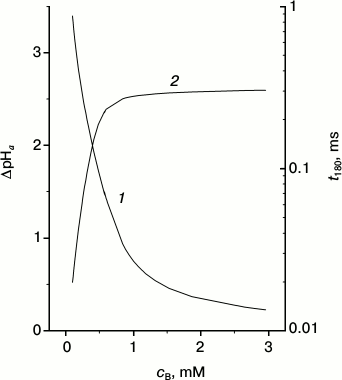
Fig. 4. Dependence of maximal ΔpHa (1) and time t180 that is required for pmf to reach –180 mV (2) at mitochondrial membrane upon buffer concentration.
At a given side of the membrane, the local change in pH is defined via the logarithm of the ratio of the current concentration to the equilibrium one in region a,
whereas the transmembrane gradient is defined as:
Figure 2 shows δpHa′ (curve 1), δpHa′′ (curve 2), and pmf (curve 3) at membrane M as functions of time counted from the moment when the pumps were turned on. At t < τa,pH = 10 µs, both δpHa′ and δpHa′′ increase in absolute magnitude, but simultaneously the pmf increases and the proton current decreases accordingly. Appreciable changes in the local pH begin at t ≈ τa,pH when pmf is still small. The competition between proton pumping and proton escape to region b results in a maximum at t ≈ 100 µs at the mobile buffer concentration of 1 mM (curves 1 and 2); the maximum sharply increases and shifts toward smaller t at concentration 0.5 mM (curves 1′ and 2′). The height of this maximum increases with increase in the relaxation time of the surface protons, t0; this time is inversely proportional to the square of the mobile buffer concentration cB (see (S21) and (S16) in the Supplement). An interesting parameter is the time to reach the value of pmf = –180 mV, which also depends on cB; these dependences are shown in Fig. 4 and Fig. S10 (see Supplement).
These results will be discussed in greater detail in the next section; here, one additional remark is necessary. Despite the fact that the time to reach the full a ↔ b equilibration at the mobile buffer concentration of 1 mM in Fig. 2 (t0 = 0.7 µs) is one order of magnitude shorter than the pHa pumping time (τa,pH = 10 µs), the transmembrane ΔpHa has enough time to increase to a value ~1 owing to the above-mentioned effect of slow relaxation. In such a case, the local pH change at the P side is much smaller than that at the N side although the membrane properties and pHb,eq are identical on both sides of the membrane. The difference is merely explained by the fact that pH is the logarithm of concentration, and the logarithm increases from a given value much more slowly than it decreases. In other words, at a given number of the pumped protons and equal volumes of regions a on both sides of the membrane (and equal proton concentrations therein), δpHa′ will increase by a larger extent than δpHa′′ decreases. The identical conditions on both sides explain why the maximum of δpHa′ and minimum of δpHa′′ occur simultaneously.
Similar curves for membrane B are shown in Fig. 3. Since the conditions at the N side did not change, the qualitative behavior of curve 1 did not change either. The decrease in its maximum compared to Fig. 2 is explained by the strongly changed conditions at the P side, thereupon the pmf at membrane B increases faster (hence, the pumps “die” earlier) than at membrane M. On the contrary, the behavior of curve 2 changes significantly because of nearly absent a ↔ b relaxation at times shorter than t0′′ ~ 104 µs (see Table 2), which would restrict the rise of δpHa′′ in absolute value at these times. As a consequence, the minimum of δpHa′′ is reached later and is deeper than in Fig. 2.
When barrier U is decreased, the characteristic times τa,pH and t0 are reduced (see Table S1 in the Supplement). This results in more efficient pumping at short times (Fig. S5 in the Supplement). In comparison, when the barrier is increased, the maximum and minimum of δpHa shift to longer times and their magnitudes decrease (Fig. S6 in the Supplement).
The lack of equivalence of two sides of the membrane has another important consequence: two local δpHa values depend on the buffer concentration differently. When the buffer concentration at the P side vanishes (membrane B; Fig. 3), the peak of |δpHa′′| on the P side increases by only a small amount, whereas the increase of δpHa′ on the N side is much more pronounced.
We also calculated the global ΔpH in the absence of the surface effect. The corresponding formulae are given in the Supplement, and the calculated results are presented in Figs. S7-S9 for mitochondria (see the Supplement). Here the distinction between the free and bound protons is of no importance, and the total buffer concentration is high. At cB = 100 mM and physiological pmf, the global ΔpH does not exceed 0.1. However, when cB ≤ 10 mM, the ΔpH can be on the order of unity.
DISCUSSION
The starting point of our analysis is formula (3), which expresses the dependence of the intensity of proton pumping upon the pmf. The remarkable feature of this formula is that it predicts the maximum attainable, limiting pmf values close to the observed (physiological) value of 200 mV. It is essential that this result was achieved without any parameter adjustments and that the limiting pmf only weakly depends on the extremely variable membrane and solution parameters. This suggests that formula (3) basically correctly describes the kinetics of pmf generation. Its shortcoming is too fast transition from the regime of intense pumping, at low pmf, to the regime of slow pumping, at high pmf, close to the physiological value. This shortcoming is removed in its modified version (formula (6)) with the introduction of one adjustable parameter, whose meaning is as follows.
Strictly speaking, the limiting pmf depends not only on the pumps, the pmf generators, but also on the pmf consumers (as well as the membrane leaks). Unfortunately, at present there are no sufficient data to model the proton current of the consumer by a formula similar to (3) or (6). It is only known with certainty that the time scale of the work of the consumers is approximately the same as that of the generators (which is obviously necessary for the self-consistent operation of the system), i.e. milliseconds. Given the uncertainties, the consumers were not explicitly included in our present model. In the future advanced models, the above-mentioned parameter can be used for a better description of time coordination of the work of the generators and consumers.
In the absence of the consumers, the pmf increases. However, the pmf buildup sharply slows when the pmf approaches its physiological value (Fig. 1). This occurs because the efficiency of the proton pumps declines very rapidly with growing pmf, which is directed against the proton pumping. In other words, the pmf is restricted by the thermodynamic limit, which is defined by the balance between the forward and backward currents. The work of the consumers at a high pmf does not affect the limiting pmf significantly. Therefore, their explicit inclusion is not critical. In what follows, when discussing the kinetic curves, we will always assume that they are restricted along the time axis by the work of the consumers.
Formulae (3) and (6) imply that the proton current depends only on the total pmf rather than on its components Δψ and ΔpH individually. As can be seen in Fig. 1, the pmf kinetics and the limiting value of the pmf only weakly depend on the parameters of the membrane and medium; this is not so for individual pmf components. However, since the details of the roles of Δψ and ΔpH in the work of the generators and consumers are not sufficiently clear at present, we will not discuss them further. Instead, in this paper we wanted to examine under which conditions one could expect generation of local or global ΔpH gradient that could significantly affect the work of the consumers. The answer depends on the composition of the medium and on the volume where the proton gradients are created. If the protons rapidly come into equilibrium with the medium, they nearly all bind to the buffers. In mitochondria, this occurs at buffer concentration on the order of 100 mM; in bacteria, the internal medium is also saturated by buffers, and the outer medium is a large volume, a “Pacific Ocean” [4]. Our calculation shows that generation of an appreciable global ΔpH can be expected only at buffer concentrations of less than 10 mM. Therefore, the main purpose of the present paper is to estimate the local ΔpH generated by the proton pumps.
We assume that a narrow, two H-bonds wide attractive water layer exists near the membrane surface (region a) that retains protons. The pumps take up protons in region a on the N side and pump them to region a on the P side. The membrane attraction creates a potential well in region a that prevents proton exchange with the adjacent bulk (region b). In region a, this gives rise to a local perturbation, δpHa, of pH from its equilibrium value (see Eq. (19)). The actual values of δpHa created by the pumps on both sides of the membrane depend on the competition of several processes. First, the increase in ΔpHa (see Eq. (20)) is accompanied by a simultaneous increase in |Δψ|; by our estimates, the increase in ΔpHa can outpace that of |Δψ|, so that a significant ΔpHa can develop before the “locking”, limiting value of pmf is reached. Second, the protons can leave region a either spontaneously, due to thermal fluctuations, or because of collisions of the mobile buffer molecules with the interface between regions a and b (it is supposed that buffer does not penetrate into region a). Obviously, large ΔpHa could arise in the case that the full lifetime of the protons in region a is longer than the rise time of ΔpHa (mechanism 1). Our estimates show, however, that mechanism 1 cannot be realized in mitochondria and neutrophilic bacteria, but there is a possibility, in principle, of its realization in alkaliphiles. Yet this possibility is not considered here because, first, the formulae for current need modification, and second, there exists a possibility for alkaliphiles to perform ATP synthesis via a sodium cycle [26].
The basic results of the present paper relate to the analysis of mechanism 2, which describes what happens with the pumped protons when they escape the attractive well on the surface. We find that the protons that left the attractive region a do not come into equilibrium with the bulk region b immediately, this requires some time necessary for diffusion over quite a long distance from the surface; this time is longer the stronger the membrane attraction. Moreover, the kinetics of depletion of the near-surface region occurs by a very slow, power law, so that the non-equilibrium proton concentration (increased at the P side and decreased at the N side) at the interface between regions a and b is preserved for a long time. The calculated results in Figs. 2-4 show that this can lead to generation of a significant local ΔpHa. The increased value of ΔpHa arises, however, only transiently, over a short time interval, after which the relaxation processes deplete the non-equilibrium protons. Figure 2 shows how the maximal ΔpHa value and the time during which the pmf is restored to its initial level depend on the concentration of the mobile buffer.
Figure 4 demonstrates the strong dependence of the maximal values of the local ΔpHa upon the mobile buffer concentration (curve 1). The largest effect is obtained at low concentrations where the time of equilibration between the surface and the bulk is long (Fig. S10 in the Supplement). It is seen that at relatively low mobile buffer concentrations, the pmf buildup basically occurs due to the surface protons, i.e. due to ΔpHa. This is easy to rationalize: in this case the protons do not leave the surface during the time of their pumping from one side of the membrane to the other. As soon as the pmf reaches the limiting value, the proton pumps sharply slow down and the proton equilibrium is restored; once equilibrium is reached, the total pmf mainly consists of its electrical component Δψ.
It is interesting to note that in parallel with the decrease of the mobile buffer concentration and with the respective increase of the contribution of the surface protons, the restoration time of the surface potential decreases. For the sake of the discussion, we define the restoration time as the time required for the pmf to reach the value of –180 mV, and we denote it t180 (curve 2). It is seen that the potential is restored about ten times faster at the low buffer concentration of 0.1 mM than at a high 1 mM. In other words, at small cB, when the surface protons play an important role, the system responds to the changes of the membrane potential very quickly, restoring the steady-state value of the potential. As a result, any potential change induced by an external source is immediately compensated by translocation of the surface protons and the membrane potential is quickly restored. Such a quick response of the membrane to a change in the external conditions results in a more stable pmf on the membrane, and hence, a more stable work of the ATP synthase. The role of the surface protons in the work of the respiratory chain described above is probably the most important result of the present work.
For reasons of mathematical convenience, following the papers by Drachev et al. [19, 20], we considered the problem of the non-equilibrium ΔpHa generation under the condition that the pumps are switched on at some initial moment of time, before which the system was resting at thermodynamic equilibrium. In reality, there is no such initial switching-on condition; rather, there is an “active” State 3, in which the intense processes of pmf generation and its consumption for ATP synthesis are occurring, and a “passive” State 4 where these processes are strongly inhibited either because of no “demand” of the organism for the ATP production or because of the lack of energy/fuel sources. Therefore, it is useful to discuss the results obtained in terms of a relation between the pmf and the pump current. Figure 1 demonstrates the obvious relation: the lower the pmf the larger the current. In Figs. 2 and 3, one should disregard the initial parts of the curves before they reach their maxima and minima, where the influence of the switching-on moment is still strong; then, the following correlation becomes noticeable. If the pmf is high, in the range of 150-250 mV, the proton pumps work slowly and cannot compete with the process of equilibration between regions a and b; this results in a decrease in the local pH changes. Alternatively, if the pmf is low, the pumps work fast and are able to create appreciable δpHa on both sides of the membrane.
Consider the transitions between States 4 and 3 from this point of view. According to the arguments presented, the pmf in State 4 is large (this is confirmed by the data for rat liver mitochondria where it is equal to 230-235 mV [2]), the local δpHas are not produced, and the system uses only Δψ and the global ΔpH, no matter how small the latter is (or it is not used at all). Now, a “request” for massive ATP production comes in by means of “injection” of massive amounts of ADP and/or phosphate. The pmf drops sharply, the pumps start to work intensely, and the local δpHas arise at both sides of the membrane, i.e. the system makes the transition to State 3. It is essential that the response of the system to these changes is nearly instantaneous: as is seen in Figs. 2-4, it takes microseconds for the current to increase after the pmf drop, which is due to a large number of pumps on the membrane. Intensive consumption of the pumped protons maintains the pmf at a low level maintaining the intensive pumping as long as the conditions for ATP production in large amounts are preserved. But as soon as these conditions are broken, the pmf increases and the system returns to State 4. These arguments assume that ΔpH is absolutely necessary for ATP synthesis in State 3.
In conclusion, we repeat the main result of our work. Under conditions where the surface protons play a role, i.e. at low enough concentration of mobile buffer, upon sudden changes in the membrane potential, they facilitate quick and neutralizing response of the membrane to such changes, resulting in stabilization of the membrane pmf and fast communication between the generators and consumers, whereas their contribution to the steady-state energetics is insignificant.
We are grateful to A. D. Vinogradov and L. S. Yaguzhinsky for valuable comments that helped us in the work. Thanks are also due to Yu. N. Antonenko, A. V. Bogachev, A. A. Konstantinov, A. B. Rubin, and the participants of the seminars at the M. V. Lomonosov Moscow State University for discussions, and to V. P. Skulachev for his interest and encouragement.
This work was supported by a grant from the Russian Foundation for Basic Research (12-03-00030a) to Medvedev and grants from NSF (PHY 0646273) and NIH (GM54052) to Stuchebrukhov.
REFERENCES
1.Soga, N., Kinoshita, K., Jr., Yoshida, M., and
Suzuki, T. (2012) J. Biol. Chem., 287, 9633-9639.
2.Nicholls, D. G. (2005) Biochim. Biophys.
Acta, 1710, 63-65.
3.Zharova, T. V., and Vinogradov, A. D. (2012)
Biochemistry (Moscow), 77, 1000-1007.
4.Williams, R. J. P. (1978) FEBS Lett.,
85, 9-19.
5.Williams, R. J. P. (1982) FEBS Lett.,
150, 1-3.
6.Williams, R. J. P. (1993) Biosci. Rep.,
13, 191-212.
7.Williams, R. J. P. (2001) ChemBioChem,
2, 637-641.
8.Kell, D. B. (1979) Biochim. Biophys. Acta,
549, 55-99.
9.Mitchell, P. (1968) Chemiosmotic Coupling and
Energy Transduction, Glynn Research, Bodmin, Cornwall.
10.Eroshenko, L. V., Marakhovskaya, A. S., Vangeli,
I. M., Semenyuk, P. I., Orlov, V. N., and Yaguzhinsky, L. S. (2012)
Doklady Biochem. Biophys., 444, 158-161.
11.Yaguzhinsky, L. S., Motovilov, K. A., Lobysheva,
N. V., Marakhovskaya, A. S., and Moiseeva, V. S. (2011) FEBS J.,
278, 378-378.
12.Antonenko, Y. N., Kovbasnyuk, O. N., and
Yaguzhinsky, L. S. (1993) Biochemistry (Moscow), 58,
684-691.
13.Antonenko, Y. N., Kovbasnjuk, O. N., and
Yaguzhinsky, L. S. (1993) Biochim. Biophys. Acta, 1150,
45-50.
14.Moiseeva, V. S., Motovilov, K. A., Lobysheva, N.
V., Orlov, V. N., and Yaguzhinsky, L. S. (2011) Doklady Biochem.
Biophys., 438, 127-130.
15.Pastore, D., Soccio, M., Laus, M. N., and Trono,
D. (2013) BMB Rep., 46, 391-397.
16.Cherepanov, D. A., Feniouk, B. A., Junge, W., and
Mulkidjanian, A. Y. (2003) Biophys. J., 85,
1307-1316.
17.Medvedev, E. S., and Stuchebrukhov, A. A. (2011)
J. Phys. Condens. Matt., 23, 234103.
18.Medvedev, E. S., and Stuchebrukhov, A. A. (2013)
FEBS Lett., 587, 345-349.
19.Drachev, A. L., Markin, V. S., and Skulachev, V.
P. (1984) Biol. Membr. (Moscow), 1, 453-477.
20.Drachev, A. L., Markin, V. S., and Skulachev, V.
P. (1985) Biochim. Biophys. Acta, 811, 197-215.
21.Widengren, J. (2013) in Fluorescence
Fluctuation Spectroscopy (Tetin, S. Y., ed.) pp. 231-252.
22.Skulachev, V. P. (1989) Energetics of
Biological Membranes [in Russian], Nauka, Moscow.
23.Skulachev, V. P., Bogachev, A. V., and
Kasparinsky, F. O. (2012) Membrane Bioenergetics [in Russian],
Lomonosov Moscow State University Publishers, Moscow.
24.Beard, D. A. (2005) PLoS Comput. Biol.,
1, 252-264.
25.Schaffhauser, D. F., Patti, M., Goda, T.,
Miyahara, Y., Forster, I. C., and Dittrich, P. S. (2012) PLoS
ONE, 7, e39238.
26.Skulachev, V. P., Bogachev, A. V., and
Kasparinsky, F. O. (2013) Principles of Bioenergetics, Springer,
Berlin.
27.Yurkov, V. I., Fadeeva, M. S., and Yaguzhinsky,
L. S. (2005) Biochemistry (Moscow), 70, 195-199.
28.Georgievskii, Y., Medvedev, E. S., and
Stuchebrukhov, A. A. (2002) Biophys. J., 82,
2833-2846.
29.Georgievskii, Y., Medvedev, E. S., and
Stuchebrukhov, A. A. (2002) J. Chem. Phys., 116,
1692-1699.
30.Medvedev, E. S., and Stuchebrukhov, A. A. (2006)
J. Math. Biol., 52, 209-234.
31.Garlid, K. D., and Paucek, P. (2003) Biochim.
Biophys. Acta, 1606, 23-41.
32.Wu, F., Zhang, J., and Beard, D. A. (2009)
Proc. Natl. Acad. Sci. USA, 106, 7143-7148.
33.Babakov, A. V., Ermishkin, L. N., and Liberman,
E. A. (1966) Nature, 210, 953-955.
34.Skulachev, V. P. (1988) Membrane
Bioenergetics, Springer, Berlin.
35.Rubin, A. B. (2000) Biophysics [in
Russian], Vol. 2, Knizhnyi Dom Universitet, Moscow.
Supplementary Material (PDF)