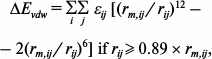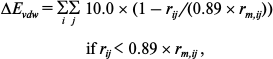Cation–pi Interactions at Non-redundant Protein–RNA Interfaces
Honggucun Zhang1, Chunhua Li1*, Feng Yang1, Jiguo Su2, Jianjun Tan1, Xiaoyi Zhang1, and Cunxin Wang1*
1College of Life Science and Bioengineering, Beijing University of Technology, Beijing 100124, China; fax: 86-10-67392837; E-mail: zhgc1988@gmail.com; chunhuali@bjut.edu.cn; fyang@bjut.edu.cn; xiaoyizhang@bjut.edu.cn; cxwang@bjut.edu.cn2College of Science, Yanshan University, Qinhuangdao 066004, China; E-mail: jiguosu@bjut.edu.cn
* To whom correspondence should be addressed.
Received December 23, 2013; Revision received March 31, 2014
Cation–pi interactions have proved to be important in proteins and protein–ligand complexes. Here, cation–pi interactions are analyzed for 282 non-redundant protein–RNA interfaces. The statistical results show that this kind of interactions exists in 65% of the interfaces. The four RNA bases are ranked as Gua > Ade > Ura > Cyt according to their propensity to participate in cation–pi interactions. The corresponding ranking for the involved amino acid residues is: Arg > Lys > Asn > Gln. The same trends are obtained based on the empirical energy calculation. The Arg–Gua pairs have the greatest stability and are also most frequently observed. The number of cation–pi pairs involving unpaired bases is 2.5 times as many as those involving paired bases. Hence, cation–pi interactions show sequence and structural specificities. For the bicyclic bases, Gua and Ade, their 5-atom rings participate in cation–pi interactions somewhat more than the 6-atom rings, with percentages of 54 and 46%, respectively, which is due to the higher cation–pi participation proportion (63%) of 5-atom rings in the paired bases. These results give a general view of cation–pi interactions at protein–RNA interfaces and are helpful in understanding the specific recognition between protein and RNA.
KEY WORDS: cation–pi interactions, protein–RNA interfaces, sequence and structural specificities, electrostatic energy, ab initioDOI: 10.1134/S0006297914070062
Abbreviations: Ade, adenine; Benz, benzene; Cyt, cytidine; Gua, guanosine; Ura, uridine.
Protein–RNA recognition plays an important role in gene expression
and regulation. The study of protein–RNA interactions is the
focus of structural and computational biology research. Thanks to
recent fast progress, the structural data from X-ray crystallography
and nuclear magnetic resonance (NMR) spectroscopy have covered all
major classes of protein–RNA complexes [1],
which makes it possible for us to try to study the general features of
protein–RNA interactions.
It has been proved that several noncovalent interactions, such as base-specific hydrogen bonds and nonpolar contacts, are essential for protein–RNA binding specificity [2]. As a kind of noncovalent interaction, cation–pi bonding has been gradually recognized as an important type of intra- and inter-molecular interaction. It has been reported that cation–pi interactions can be very strong in biomolecular systems [3-5]. In some cases, they are even comparable to electrostatic interactions, van der Waals interactions, and hydrogen bonds [6]. They make considerable contributions to the folding and stability of proteins [7-9] and specific molecular recognition [10-15]. Therefore, cation–pi interactions have non-negligible importance and have been considered as one of the major forces for molecular recognition [3, 16, 17].
In recent years, much attention has been paid to the study of cation–pi interactions in protein, protein–protein, and protein–DNA complexes. For protein and protein–protein complexes, cation–pi interactions have been found to be critical for execution of function of many kinds of biosystems, such as ion channels [18], G-protein-coupled receptors [19], transporters [10, 13], and enzymes [20]. Gallivan and Dougherty [21] made statistical analyses for a dataset of 68 proteins and found that as the cationic group, the side chain of Arg takes part in cation–pi interactions twice as often as that of Lys. Additionally, it has been proved that the electrostatic energies of cation–pi pairs determine their trends in binding ability [22]. For protein–DNA complexes, cation–pi interactions exist widely at their interfaces [23, 24]. Wintjens [23] and Gromiha [24] found that there are different preferences for different amino acid residues and DNA bases in forming cation–pi interactions. Arg and Lys, providing cationic groups, are observed to be more favorable for cation–pi interactions than Asn and Gln. Gua and Ade, providing aromatic rings, are more favorable than Cyt and Thy. Additionally, for the bicyclic bases, Gua and Ade, nearly 90% of the cation–pi interactions are formed through their 5-atom rings.
For protein–RNA complexes, there are few works concerning the general features of cation–pi interactions at interfaces. Recently, one published work regarding the statistical properties of cation–pi interactions at 48 protein–RNA interfaces appeared [25]. Besides relatively fewer structures of protein–RNA complexes, the similar component unit of RNA and DNA, we think, is another reason for this status. Currently, structural data on protein–RNA complexes have increased greatly, and it has become possible for us to try to study the general features of protein–RNA interactions. Additionally, although RNA is similar to DNA in sequence, they are dramatically different in overall structure. DNA is usually a perfect double-stranded helical molecule, while the structure of RNA is more complicated. In some cases, RNA is a single-stranded molecule, but in most cases (especially in the ribosome) RNA structures are constructed by perfect or distorted A-helices and short single-stranded regions. Their difference in structure may result in the differences in their participation in cation–pi interactions with protein.
In this work, we analyzed the cation–pi interactions for 282 non-redundant protein–RNA interfaces. First, we performed ab initio quantum mechanics calculations on Na+–RNA base complexes. The results yielded a comparison of the magnitude of cation–pi interactions for the four different bases, using benzene (Benz) as a reference molecule. Then the potential cation–pi interactions were identified, and empirical energy calculations were done to compare the trends of binding energies for different cation–pi pairs. We found several differences in cation–pi interactions between protein–DNA interfaces and protein–RNA interfaces. This work is helpful in understanding of the physical nature of cation–pi interactions at protein–RNA interfaces.
MATERIALS AND METHODS
Ab initio calculations for interaction energies of Na+–RNA base complexes. To get a basic understanding of cation–pi interactions involving RNA bases, the binding strengths were first investigated for Na+–RNA base complexes with the Na+–Benz complex used as a reference. The Gaussian 03 suite of programs [26] was used for ab initio computations. Initial geometries of molecular fragments such as the benzene and isolated aromatic rings of Ade, Cyt, Gua, and Ura RNA bases were built and optimized at the HF (Hartree–Fock) level. A methyl group was used to replace the main chain and was attached to the N1 atom of Cyt and Ura, and to the N9 of Gua and Ade.
The Na+ was approached towards the center of the aromatic ring perpendicularly to the molecular plane. The distance between Na+ and the aromatic ring was taken as dNa+. Both rings of bicyclic bases (Ade, Gua) were considered, respectively. For each case the interaction energy was calculated at HF/6-31G** level on a one-dimensional grid of nine points corresponding to distances dNa+ ranging from 2 to 6 Å. With the approach of Na+ to the aromatic ring, the geometry of the aromatic system was not optimized, but it was frozen at its initial optimized equilibrium geometry. The value of dNa+ that minimizes the interaction energy is dmin-Na+. This method has been used in the study of cation–pi interactions at protein–DNA complexes [23].
Afterwards, Na+–aromatic interaction energy maps were computed by moving the Na+ in a plane parallel to the aromatic ring at the fixed distance dmin-Na+. We obtained each map by interpolating the interaction energy calculated at the nodes of a square lattice of 100 × 100 points corresponding to the positions of the Na+ in the plane parallel to the aromatic ring. The square lattice was centered on the barycenter of the aromatic system and the square size of 8 × 8 Å was used. Interaction energy calculations were performed using the DFT (Density Functional Theory) method with the larger 6-31++G** basis set and were corrected for the BSSE (Basis Set Superposition Error) by using the standard function counterpoise method. The interaction energy ΔEDFT was calculated as follows:
ΔEDFT = E(A–B) – E(A; A–gB) – E(B; gA–B),(1)
where E(A–B) is the energy of the A–B complex, and E(A; A–gB) is the energy of the isolated molecule A calculated in the presence of ghost B, which is defined by its basis set functions but does not contain any electron or proton.
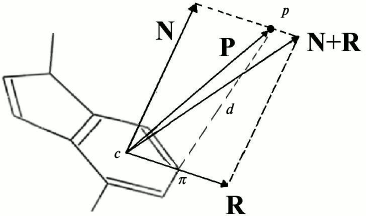
Definition of cation–pi interactions. A geometric definition of cation–pi interactions, used in a previous study for protein–DNA interactions [23], was adopted to detect potential cation–pi interactions at protein–RNA interfaces. This definition, consisting of a distance and an angle criterion, is illustrated in Fig. 1. First the atoms of amino acids that carry the positive charge (CZ and CD for Arg, NZ and CE for Lys) or the partial positive charge (NE2 and CD for Gln, ND2 and CG for Asn) [21, 23, 24] are denoted by p. The atoms of aromatic rings that are spatially closest to these positively charged atoms are marked with π. The distance criterion is that the distance d between the atoms p and π cannot be larger than 4.5 Å. The role of the angle criterion is to ensure that the positive charge is located above the plane of the aromatic ring rather than in that plane. For this purpose, the angle between vector P and N cannot be larger than that formed by vector N and (N + R). The vectors P, R, and N all have the center c of the aromatic ring as the start point. P links c with the positive charged atoms p, R contains the ring atom π, and its length is twice the largest distance between c and the atoms of the ring, while N is normal to the ring and its length equals the distance between p and π.
Fig. 1. Geometric criteria used to detect potential cation–pi interactions between positively charged groups and aromatic pi-systems. Point p and π denote the cationic charge and the atom of the aromatic cycle that is closest to p, respectively; the distances d between them are not larger than 4.5 Å. Point c is the center of the ring. The vectors N, P, and R all have the center c as the start point. P links c with the positive charge p, R contains the ring atom π, and its length is twice the largest.
Empirical energy calculations of cation–pi interaction energy. To obtain an energy analysis of cation–pi interactions at protein–RNA interfaces, we performed empirical energy calculations on different cation–pi pairs and compared their formation trends. The Amber 10 force field [27] was used to compute the cation–pi interaction energy.
Although empirical methods cannot provide an accurate energy calculation for the cation–pi interaction, it can still give the trend in the interaction energy [21]. Therefore, we used the empirical energy calculation to estimate the binding energy ΔEtotal of different cation–pi pairs:
ΔEtotal = ΔEele +ΔEvdw. (2)
The empirical energy includes electrostatic and van der Waals’ interaction energies. The electrostatic interaction energy ΔEele was computed as follows [28]:
ΔEele = ∑(322qiqj/εrij), (3)
where qi and qj are the charges of atoms i and j, respectively, and rij is the distance between them. The distance-dependent dielectric constant (ε = rij) is used to take account of the dielectric damping effect of the Coulomb interactions. The van der Waals’ energy (ΔEvdw) was computed as follows [29]:
where rm,ij is the sum of the Lennard–Jones radii of atoms i and j of the two interactive molecules, rij is the distance between the two atoms, εij is the square root of the product of the well depths, ΔEvdw is continuous at rij = 0.89 rm,ij.
Protein–RNA interaction data set. We selected a data set of 282 non-redundant protein–RNA interactions from reference [30] for the analysis of cation–pi interactions between nucleic acid base rings and positively charged groups of Lys and Arg and partially charged groups of Asn and Gln. The coordinates of all the protein–RNA complex structures are taken from the PDB (Protein Data Bank) [31].
Comparison of the datasets used in this work and the published article. It is noted that there are some differences between the datasets used in this work and the reference [25]. First, in reference [25] no NMR structures were accepted, while they are included in ours. Second, only crystal structures with resolution of 2.0 Å or better are accepted in theirs, while the resolution of structures are not concerned in ours. Finally, polypeptides and polyribonucleotides are required to be longer than 20 amino acids and 5 nucleotides, respectively, in theirs, while in ours only polyribonucleotides are guaranteed to be longer than 5 nucleotides. As a result, our dataset contains 282 protein–RNA interactions (from 144 protein–RNA complexes) and theirs is composed of 59 protein–RNA complexes with only 13 complexes shared in both datasets. It is clear that ours contains more structures, while theirs includes the structures with higher resolutions. Although there are some differences between the two datasets, most of the results are similar. With the development of protein–RNA complex structure study, we believe that more and more structures with higher resolution will be obtained, which will be helpful for the reasonability and reliability of statistical analyses on protein–RNA interactions.
RESULTS AND DISCUSSION
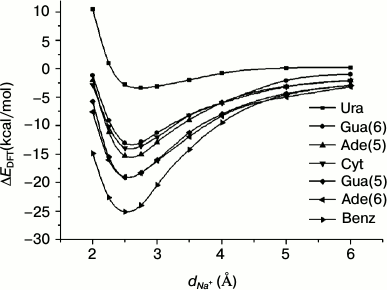
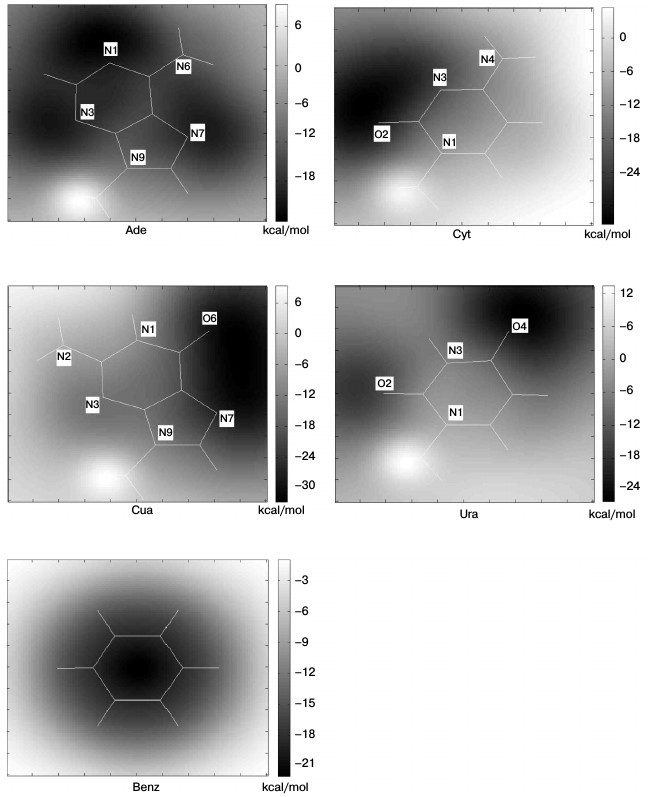
Ab initio energy calculations on Na+–RNA base complexes. Before the analysis of cation–pi pairs at protein–RNA interfaces, we studied the energy of Na+–RNA base complexes as a function of the distance dNa+ between Na+ and the center of the aromatic ring, and we compared the result with that obtained for Na+–Benz complexes (Fig. 2). Gua(5), Ade(5) and Gua(6), Ade(6) represent the 5-atom and 6-atom rings of Gua and Ade, respectively. During this process the Na+ will approach along the axes passing through the centers of different rings and perpendicular to the planes. This distance changes from 6 to 2 Å. The interaction energies were computed at the HF level using the 6-31G** basis set and were corrected for the basis set superposition error BSSE (see “Materials and Methods”). From Fig. 2, it is evident that for all the aromatic rings, there exist a minimum in the interaction energy curve at a value of dNa+ close to 2.5 Å. At this distance, interaction energy maps were calculated for Na+–RNA base and Na+–Benz complexes (Fig. 3) according to Eq. (1) with the Na+ located at the nodes of an 8 × 8 Å square lattice lying in a plane parallel to the aromatic ring at the distance of 2.5 Å.
Fig. 2. Interaction energies of Na+–RNA base complexes computed at HF/6-31G** (BSSE) level. dNa+ is the distance between the Na+ and the center of the aromatic ring of the RNA base. Gua(5), Ade(5) and Gua(6), Ade(6) represent the 5-atom and 6-atom rings of Gua and Ade, respectively. The Na+–Benz complex is used as a reference.
Fig. 3. Interaction energy maps computed by the DFT-B3LYP method at the B3LYP/6-31++G** (BSSE) level for the four Na+–RNA base complexes and Na+–Benz. The Na+ is placed on a plane parallel to the ring and the distance between the plane and ring is 2.5 Å.
From Fig. 3, the Na+–Benz energy map is symmetric with energy minimum above the center of the ring. However, Na+–RNA base energy maps are asymmetric and much more complex due to the strong disturbance of heteroatoms. The energy minima tend to be localized above electronegative heteroatoms: the atoms N1, N3, and N7 for Ade, O2 and O4 for Ura, O6 and N7 for Gua, and O2 and N3 for Cyt. This suggests the importance of the electrostatic interactions in Na+–RNA base complexes. Although the energy minima are transferred relative to the ring center, the interactions still remain favorable with energies ranging from about –10 to –20 kcal/mol for Ade, Gua, and Cyt, and –10 to 0 kcal/mol for Ura. Additionally, it can be seen that the regions above the methyl groups show unfavorable energy. This is caused by the repulsive steric clashes between the Na+ and the hydrogen atoms attached to the methyl.
We extracted the interaction energy values between different aromatic rings and Na+ located over the centers of the rings from Fig. 3, and these values are shown in Fig. 4. The interaction energy for Gua(5) is similar to that for Ade(6), with the values of –19.83 and –19.20 kcal/mol, respectively, which are the lowest among all the rings of RNA bases. And for Ade(5), Gua(6), and Cyt, the interaction energies are similar to each other, with values of –15.27, –14.77, and –14.31 kcal/mol, respectively. The ring having the least favorable interaction energy with Na+ is Ura, –4.25 kcal/mol. As a comparison, the interaction energy for Na+–Benz is about –23 kcal/mol. These results reflect the different trends (Eq. (6)) for different aromatic rings to form cation–pi interactions with Na+ over their centers:
–ΔEDFT {Benz > Gua(5) ≈ Ade(6) > Ade(5) ≈ Gua(6) ≈ Cyt > Ura}. (6)
This trend agrees with a previous study [23] of cation–pi interactions at protein–DNA interfaces for the common bases. To compare the trends of Ura and Thy to form cation–pi interactions with Na+, we calculated the interaction energy between Thy and Na+ using the same method. The result is –3.32 kcal/mol, and the corresponding energy for Ura is –4.25 kcal/mol, which suggests that Ura might be more favorable for forming cation–pi interactions. The main difference between Ura and Thy is the atom attached to atom C5: a methyl in Thy and a hydrogen in Ura. The electrostatic clash between methyl and Na+ is stronger than that between hydrogen and Na+, which is the main reason for the energy difference.
Fig. 4. Interaction energies between different aromatic rings and Na+ located over their centers.
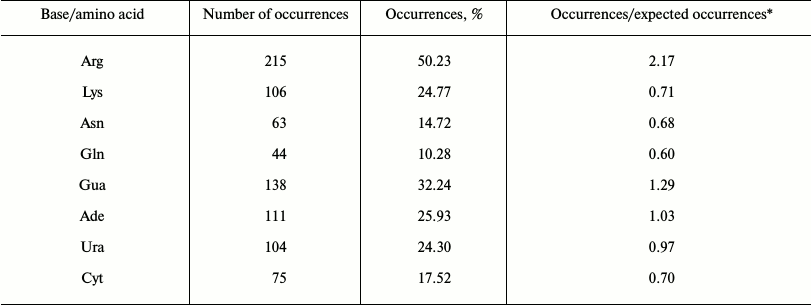
Statistical analysis of cation–pi interactions at protein–RNA interfaces. We performed a statistical analysis of cation–pi interactions at the 282 non-redundant protein–RNA interfaces. The potential cation–pi interactions between positively charged amino acid side chains and RNA bases were identified by the distance and angle criteria defined in “Materials and Methods”. The occurrence frequencies of cation–pi interactions involving different bases and amino acids are listed in Table 1. We identified 428 cation–pi interactions at these interfaces, and found that 55% of the interfaces contain at least one potential cation–pi interaction between a positively charged residue (Arg or Lys) and an RNA base. If Asn and Gln residues are also considered, this percentage will rise to 65%. This indicates the cation–pi interaction is very common at protein–RNA interfaces. In protein–DNA complexes [23], the corresponding percentages are 59 and 71%, respectively, that seem a little higher than those at protein–RNA interfaces. It should be noted that our statistics is for interfaces, not for complexes that were used in the protein–DNA study. Considering that one complex may have several interfaces, this result is not difficult to understand.
Table 1. Occurrence frequencies of
cation–pi interactions involving different bases and amino
acids
* The expected occurrences of cation–pi pairs were computed by the
method used in reference [23].
From Table 1, the Arg residues are involved in about 50% of cation–pi interactions. It is the highest, followed by Lys, Asn, and Gln involved in about 25, 15, and 10% of cation–pi interactions, respectively. After the expected occurrences are considered, the trend of the four residues in forming cation–pi interactions remains the same (see the fourth column in Table 1). The result that Arg participates in cation–pi interactions nearly twice as often as Lys agrees well with the situation in protein structures [21, 32] and protein–DNA complexes [24]. A possible reason is that there are two terminal nitrogen atoms in the side chain of Arg, while there is only one in Lys. Nitrogen atoms have a strong ability to attract electrons, which makes the atoms connected to them carry positive charges. Thus, Arg residues have a stronger protonation capability than Lys, and therefore can form more stable cation–pi interactions. In the protein–RNA work [25], no significant differences were observed for Arg and Lys in forming cation–pi interactions. The higher protonation levels of Arg and Lys compared to Asn and Gln, we think, are the main reason for the higher occurrences of Arg and Lys than Asn and Gln. Concerning RNA bases, Gua is observed in about 32% of the cation–pi interactions, 26% for Ade, 24% for Ura, and 18% for Cyt. Thus, the occurrence frequencies of RNA bases in cation–pi interactions can be ranked as follows:
Freq. {Gua > Ade > Ura > Cyt}. (7)
After the expected occurrences are taken into account, the fourth column in Table 1 gives the propensities of RNA bases to form cation–pi interactions. We can see that the propensities of purine bases Gua and Ade appear to be stronger than those of pyrimidine bases Ura and Cyt. This is consistent with the result in Fig. 4, where it can be seen that purine bases are more favorable in energy for forming cation–pi interactions than pyrimidine bases. In reference [25], a similar result was found. In addition, further analysis revealed that for cation–pi pairs involving purines (Gua or Ade), 54% are formed through 5-atom rings and 46% through 6-atom rings. This is quite different from the situations in protein–DNA complexes [23], where the corresponding percentages are 90 and 10%, respectively. We know that some ribonucleotides of RNA are unpaired, and both rings of unpaired purines have nearly the same solvent accessibility, forming almost the same number of cation–pi interactions (49% through 5-atom ring and 51% 6-atom ring). However, for the paired purines in double-stranded RNA, their 5-atom rings close to the backbone are more accessible to the solvent than 6-atom rings, and thus more cation–pi interactions are formed through 5-atom rings than 6-atom rings, with the percentages 63 and 37%, respectively. For DNA, it is usually in a double helix conformation, and thus the 5-atom rings of DNA purines are much more accessible to the solvent than the 6-atom rings. Therefore, the majority of cations are located above the 5-atom rings of DNA purine bases. The analyses above can explain the proportion difference of cation–pi interactions formed through the two rings of purines between RNA and DNA. Additionally, we notice that Ura is involved in more cation–pi interactions than Cyt, while Eq. (6) shows that Cyt is more favorable in energy for forming cation–pi interactions than Ura. The reason is possibly that in Eq. (6), the Na+ is located over the center of the ring at a distance of 2.5 Å, but in the context of protein–RNA interfaces the cationic atoms are not at that position in most cases. A similar situation also appears in the study of cation–pi interactions for protein–DNA complexes [23].
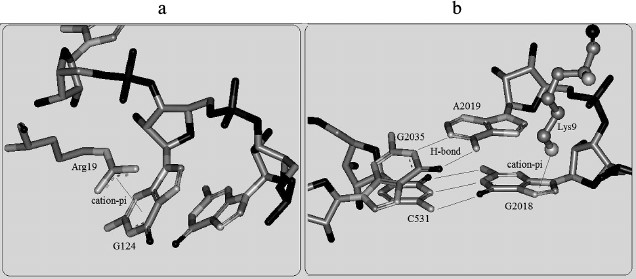
The propensities of RNA secondary structures for cation–pi interactions. To detect the propensities of RNA secondary structures for cation–pi interactions, we analyzed and compared the cation–pi interactions involving paired bases and unpaired bases. It is observed that the number of unpaired bases involved in cation–pi interactions is about 2.5 times (307 : 121) more than that of the corresponding paired ones. This phenomenon can be explained as follows. We know that the bases located in stacking interactions are practically inaccessible to cations. In RNA, most paired bases are located inside stacks, especially for the paired ones in a helix. This is why paired bases appear to be less favorable for forming cation–pi interactions than unpaired ones. Figure 5 shows an example of cation–pi interactions involving unpaired and paired bases. These indicate that the structure of RNA has an important influence on cation–pi formations. In the previous protein–RNA study, a similar situation has been found for protein secondary structures [25]. Hence, it is clear that the formation of cation–pi interactions show specificity for sequence and structures.
Fig. 5. Cation–pi interactions involving unpaired and paired bases. a) The cation–pi interaction between Arg19 of chain 7 and G124 of chain A in protein–RNA complex 2j01. b) The cation–pi interaction between Lys9 of chain 5 and G2018 (paired with C531) of chain A in protein–RNA complex 2j01.
Empirical interaction energies of different cation–pi pairs. To further analyze and compare the stability of different cation–pi pairs, the empirical energy calculation was carried out by Eq. (2) mentioned in “Materials and Methods”, and the average energies of different cation–pi pairs are listed in Table 2. The calculation was limited to the cation–pi interactions involving Arg or Lys residues because they take part in about 75% of the identified cation–pi pairs (see Table 1).
From Table 2, purine bases Ade and Gua generally form more stable cation–pi interactions than the pyrimidine bases Cyt and Ura. Arg–Gua and Arg–Ade are the two strongest cation–pi interactions, with the energy values –5.05 and –3.01 kcal/mol, respectively. The interaction energies of cation–pi pairs involving Ura are weaker than those involving Gua or Ade. The unfavorable interactions are Arg–Cyt and Lys–Cyt pairs, with energy values 0.86 and 0.80 kcal/mol, respectively. This trend for RNA bases in forming cation–pi interactions with Arg and Lys residues agrees well with the statistical result shown in Eq. (7) and is consistent with the corresponding trend obtained in reference [25]. Additionally, it is noted that electrostatic energies contribute much more to empirical energies of cation–pi interactions than van der Waals’ energies, which is the same as previous studies [21, 23, 27]. This result indicates that the electrostatic energy contributes to the major part of cation–pi interactions.
Table 2. Average energies of cation–pi
interactions between amino acids and RNA bases (in kcal/mol)

Note: The standard deviations are given in parentheses.
* ΔEele, electrostatic energy.
** ΔEvdw, van der Waals energy.
*** ΔEtotal, total interaction energy.
To ascertain the contributions of different cationic groups to the formation of cation–pi interactions, we then calculated the interaction energies of cation–pi pairs involving different cationic groups (atoms CZ and CD in Arg, NZ and CE in Lys). The results are shown in Table 3. Due to unfavorable interactions, the results for the pairs involving Cyt are not listed. From Table 3, the contributions of CZ in Arg and NZ in Lys are much greater than those of CD in Arg and CE in Lys. Arg (CZ)–Gua presents the minimal energy –5.05 kcal/mol, followed by Lys (NZ)–Gua with energy –3.42 kcal/mol. As for the atoms CD and CE, the minimal energies are –0.52 and –1.06 kcal/mol, respectively. One reason for the difference in contributions of different cationic groups may be from the amount of positive charge carried by cationic groups. Atoms CZ and NZ carry most of the positive charge of Arg and Lys, respectively. The cationic groups bearing more positive charge will provide a stronger electrostatic energy. Overall, the result indicates that the cationic groups are very important in determining the size of cation–pi interactions.
Table 3. Average interaction energies of
cation–pi pairs involving different cationic groups
(in kcal/mol)
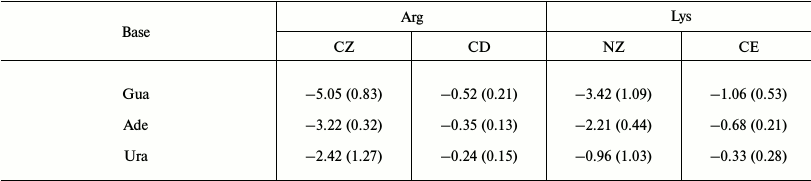
Note: The standard deviations are given in parentheses.
In this work, cation–pi interactions at 282 protein–RNA interfaces were systematically analyzed. We found that there are cation–pi interactions in 65% of the interfaces. The statistical analyses indicate that according to the propensities to form cation–pi interactions, amino acids are ranked as Arg > Lys > Asn > Gln and bases are ranked as Gua > Ade > Ura > Cyt. The empirical energy calculations also produce the same trends and show that electrostatic energy contributes to the major part of cation–pi interactions. The cation–pi interactions of Arg–Gua pairs are the most stable and the cation–Cyt pairs have unfavorable energies. For purine bases, somewhat more cation–pi interactions are formed through 5-atom rings than those through 6-atom rings, with percentages 54 and 46%, respectively. Additionally, it was found that unpaired bases take part in cation–pi interactions 2.5 times as often as paired bases. The cation–pi interactions show specificity to sequence and structures. All these results are helpful to understand the mechanism of protein–RNA specific recognition.
This work was supported by the Chinese Natural Science Foundation (Grant Nos. 31171267, 11204267, 21173014, 31100523), the Beijing Municipal Education Commission (Grant No. KM201310005030), and the Fundamental Research Fund for the Beijing Municipal Education Commission Science and Technology Innovation Platform.
REFERENCES
1.Perez-Canadillas, J. M., and Varani, G. (2001)
Recent advances in RNA–protein recognition, Curr. Opin.
Struct. Biol., 11, 53-58.
2.Draper, D. E. (1999) Themes in RNA–protein
recognition, J. Mol. Biol., 293, 255-270.
3.Salonen, L. M., Ellermann, M., and Diederich, F.
(2011) Aromatic rings in chemical and biological recognition:
energetics and structures, Angew. Chem. Int. Ed. Engl.,
50, 4808-4842.
4.Singh, N. J., Min, S. K., Kim, D. Y., and Kim, K.
S. (2009) Comprehensive energy analysis for various types of
π-interaction, J. Chem. Theory Comput., 5,
515-529.
5.Kumpf, R. A., and Dougherty, D. A. (1993) A
mechanism for ion selectivity in potassium channels: computational
studies of cation–π interactions, Science, 261,
1708-1710.
6.Priyakumar, U. D., Punnagai, M., Krishna Mohan, G.
P., and Sastry, G. N. (2004) A computational study of cation–π
interactions in polycyclic systems: exploring the dependence on the
curvature and electronic factors, Tetrahedron, 60,
3037-3043.
7.Dougherty, D. A. (1996) Cation–pi
interactions in chemistry and biology: a new view of benzene, Phe, Tyr,
and Trp, Science, 271, 163-168.
8.Dougherty, D. A. (2007) Cation–pi
interactions involving aromatic amino acids, J. Nutr., 137
(Suppl. 1), 1504S-1508S; discussion 1516S-1517S.
9.Gromiha, M. M. (2005) Distinct roles of
conventional noncovalent and cation–π interactions in protein
stability, Polymer, 46, 983-990.
10.Pless, S. A., Hanek, A. P., Price, K. L., Lynch,
J. W., Lester, H. A., Dougherty, D. A., and Lummis, S. C. (2011) A
cation–π interaction at a phenylalanine residue in the glycine
receptor binding site is conserved for different agonists, Mol.
Pharmacol., 79, 742-748.
11.Michael, L. A., Chenault, J. A., Miller, III, B.
R., Knolhoff, A. M., and Nagan, M. C. (2009) Water, shape recognition,
salt bridges, and cation–pi interactions differentiate peptide
recognition of the HIV Rev-responsive element, J. Mol. Biol.,
392, 774-786.
12.Yamashita, S., Nagata, T., Kawazoe, M., Takemoto,
C., Kigawa, T., Guntert, P., Kobayashi, N., Terada, T., Shirouzu, M.,
Wakiyama, M., Muto, Y., and Yokoyama, S. (2011) Structures of the first
and second double-stranded RNA-binding domains of human TAR RNA-binding
protein, Protein Sci., 20, 118-130.
13.Lummis, S. C. R., McGonigle, I., Ashby, J. A.,
and Dougherty, D. A. (2011) Two amino acid residues contribute to a
cation–π binding interaction in the binding site of an insect
GABA receptor, J. Neurosci., 31, 12371-12376.
14.Xiu, X., Puskar, N. L., Shanata, J. A. P.,
Lester, H. A., and Dougherty, D. A. (2009) Nicotine binding to brain
receptors requires a strong cation–pi interaction, Nature,
458, 534-537.
15.Tantry, S., Ding, F. X., Dumont, M., Becker, J.
M., and Naider, F. (2010) Binding of fluorinated phenylalanine
alpha-factor analogues to Ste2p: evidence for a cation–pi binding
interaction between a peptide ligand and its cognate G protein-coupled
receptor, Biochemistry, 49, 5007-5015.
16.Dougherty, D. A. (2013) The cation–π
interaction, Acc. Chem. Res., 46, 885-893.
17.Mahadevi, A. S., and Sastry, G. N. (2013)
Cation–π interaction: its role and relevance in chemistry,
biology, and material science, Chem. Rev., 113,
2100-2138.
18.Okada, A., Miura, T., and Takeuchi, H. (2001)
Protonation of histidine and histidine–tryptophan interaction in
the activation of the M2 ion channel from influenza a virus,
Biochemistry, 40, 6053-6060.
19.Boks, G. J., Tollenaere, J. P., and Kroon, J.
(1997) Possible ligand–receptor interactions for NK1 antagonists
as observed in their crystal structures, Bioorg. Med. Chem.,
5, 535-547.
20.Ma, J. C., and Dougherty, D. A. (1997) The
cation–π interaction, Chem. Rev., 97,
1303-1324.
21.Gallivan, J. P., and Dougherty, D. A. (1999)
Cation–pi interactions in structural biology, Proc. Natl.
Acad. Sci. USA, 96, 9459-9464.
22.Mecozzi, S., West, A. P., Jr., and Dougherty, D.
A. (1996) Cation–pi interactions in simple aromatics:
electrostatics provide a predictive tool, J. Am. Chem. Soc.,
118, 2307-2308.
23.Wintjens, R., Lievin, J., Rooman, M., and
Buisine, E. (2000) Contribution of cation–π interactions to
the stability of protein–DNA complexes, J. Mol. Biol.,
302, 395-410.
24.Gromiha, M. M., Santhosh, C., and Suwa, M. (2004)
Influence of cation–pi interactions in protein–DNA
complexes, Polymer, 45, 633-639.
25.Borozan, S. Z., Dimitrijevic, B. P., and
Stojanovic, S. D. (2013) Cation–π interactions in high
resolution protein–RNA complex crystal structures, Comput.
Biol. Chem., 47, 105-112.
26.Frisch, M. J., Trucks, G. W., Schlegel, H. B., et
al. (2003) Gaussian 03, Revision B.05, Gaussian, Inc., Pittsburgh,
PA.
27.Case, D. A., Darden, T. A., Cheatham, III, T. E.,
Simmerling, C. L., Wang, J., Duke R. E., Luo, R., Crowley, M., Walker,
R. C., Zhang, W., Merz, K. M., Wang, B., Hayik, S., Roitberg, A.,
Seabra, G., Kolossvary, I., Wong, K. F., Paesani, F., Vanicek, J., Wu,
X., Brozell, S. R., Steinbrecher, T., Gohlke, H., Yang, L., Tan, C.,
Mongan, J., Hornak, V., Cui, G., Mathews, D. H., Seetin, M. G., Sagui,
C., Babin, V., and Kollman, P. A. (2008) AMBER 10, University of
California, San Francisco, CA.
28.Gray, J. J., Moughan, S. E., Wang, C.,
Schueler-Furman, O., Kuhlman, B., Rohl, C. A., and Baker, D. (2003)
Protein–protein docking with simultaneous optimization of rigid
body displacement and side chain conformations, J. Mol. Biol.,
331, 281-299.
29.Kuhlman, B., and Baker, D. (2000) Native protein
sequences are close to optimal for their structures, Proc. Natl.
Acad. Sci. USA, 97, 10383-10388.
30.Perez-Cano, L., and Fernandez-Recio, J. (2010)
Optimal protein–RNA area, OPRA: A propensity-based method to
identify RNA-binding sites on proteins, Proteins, 78,
25-35.
31.Berman, H. M., Westbrook, J., Feng, Z.,
Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N., and Bourne,
P. E. (2000) The Protein Data Bank, Nucleic Acids Res.,
28, 235-242.
32.Minoux, H., and Chipot, C. (1999) Cation–pi
interactions in proteins: can simple models provide an accurate
description? J. Am. Chem. Soc., 121, 10366-10372.