REVIEW: A Thermodynamic and Theoretical View for Enzyme Regulation
Qinyi Zhao
Medical Institute, CRRC, POB 2619, Beijing 100068, PR China; E-mail: qinyizhao@gmail.com; qinyi_zhao@163.com
Received May 8, 2014; Revision received August 26, 2014
Precise regulation is fundamental to the proper functioning of enzymes in a cell. Current opinions about this, such as allosteric regulation and dynamic contribution to enzyme regulation, are experimental models and substantially empirical. Here we proposed a theoretical and thermodynamic model of enzyme regulation. The main idea is that enzyme regulation is processed via the regulation of abundance of active conformation in the reaction buffer. The theoretical foundation, experimental evidence, and experimental criteria to test our model are discussed and reviewed. We conclude that basic principles of enzyme regulation are laws of protein thermodynamics and it can be analyzed using the concept of distribution curve of active conformations of enzymes.
KEY WORDS: enzyme regulation, thermodynamics, active conformation, distribution curveDOI: 10.1134/S0006297915010010
Abbreviations: KNF, Koshland–Nemethy–Filmer; MWC, Monod–Wyman–Changeux; REC, regulator–enzyme complex.
Enzyme regulation is central for biological processes, and our current
understanding of it was established based on allosteric regulation
mechanism. The allosteric mechanism was developed on the cooperation
concept that was first proposed in the study of cooperative binding
between hemoglobin and oxygen [1-3]. In the past, great achievements have been made
under the name of allosteric regulation. But at fundamental level, it
is an experimental model, and all explanations established on its basis
are doomed to be empirical; therefore, dispute about it cannot be
avoided, which can be clearly seen between the
Monod–Wyman–Changeux (MWC) and
Koshland–Nemethy–Filmer (KNF) models [2, 3]. It is a well-established
fact that enzyme regulation is related to protein dynamics (or protein
flexibility, thermodynamics), but this relation (thermodynamic
mechanism for enzyme regulation) cannot be analyzed based on an
allosteric regulation mechanism. It cannot give a quantitative
description of enzyme regulation as well. So a pure theoretical model
is needed to resolve such problems.
In the past 10 years, the idea of dynamic regulation of enzyme activity has attracted much attention, and this approach has offered many valuable views about enzyme regulation [4-10]. However, because the relationship between protein dynamics and thermodynamics has not been resolved theoretically, this impedes the formulation of a theoretical model of protein regulation from such approaches.
Fortunately, the relation between protein dynamics and thermodynamics has been recently resolved [11-14]. This enables us to formulate a dynamic model for enzyme action and an allodynamic regulation model for protein regulation [15, 16]. This is a purely theoretical and thermodynamic model for protein regulation, and many theoretical questions have been resolved. The key thought is that protein dynamics could be influenced by many factors, physical or chemical, and a change in protein dynamics can alter the abundance of active conformations of an enzyme in solution, and thus enzyme regulation could be processed. The theoretical foundation, evidence, and some problems concerning it are discussed in this paper.
BASIC CONCEPTS AND THEORY
To obtain a comprehensive understanding of the thermodynamic mechanism of enzyme regulation, we first summarize basic facts and concepts of the theory.
1. In solution, any enzyme or protein exists in many conformations, and most of them are inactive. The equilibrium among them is determined by the thermodynamic principle. In the simplest case, there is only one active conformation of the enzyme.
2. The abundance of protein conformations is changeable under different conditions, and they are under a thermal equilibrium state. The abundance of one conformation can be calculated from data on protein conformational stability by applying the concept of a partition function of protein conformation [14].
3. The thermodynamic state of one conformation, such as energetic level, is also changeable under different conditions [14].
4. A change in protein dynamics can be transmitted with different degrees into other sites of a protein by thermodynamic reorganization among different parts within it, which may elicit a conformational change at other sites of a protein, but conformational change is not essential.
5. Any factors such as temperature, solvent, substrate, drug, positive and negative regulator (activator or inhibitor), or genetic mutant take their effect by influencing protein conformation stability (protein flexibility or dynamics) of enzymes, which controls the abundance of active conformations and thermodynamic state of the active conformations. Correspondently, there are two related mechanisms for enzyme regulation by these factors. First, these factors alter the thermodynamic state of each conformation of an enzyme. Second, as a result, the redistribution of thermodynamic state changes abundance of active conformations and therefore catalytic activity.
6. Effects of diversified regulators on enzyme regulation could be integrated thermodynamically within an enzyme molecule. We will not discuss it here for it also obeys the basic principles of enzyme regulation.
A major difference between our model and current opinion of dynamic contribution to enzyme regulation is that within our model a change in protein dynamics does not directly influence enzyme activity, and it takes their effect in enzyme regulation by influencing the abundance of active conformations of enzymes.
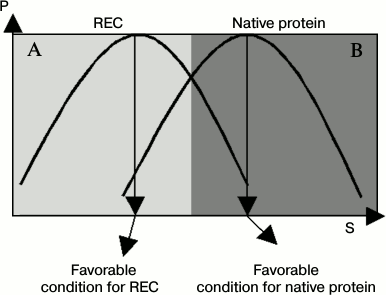
The distribution curve (or abundance curve) of active conformations of enzymes is an important concept, and the nature of a regulator can be clearly judged by comparing differences in active conformation curves between naked enzyme and a regulator–enzyme complex (REC). In this case, the REC can be considered as a new protein species. Compared with naked enzyme, the active conformation curve is shifted to another position under certain working conditions. This was named conformation shift along working conditions and was supported by many experimental tests [17-21].
Figure 1 gives diagrams of an active conformation distribution curve of both native enzyme and regulator–enzyme complex. In Fig. 1, we can clearly see that a regulator acts as a positive regulator under conditions of area A and a negative regulator under conditions of area B when the native enzyme activity acts as the reference. In other words, the regulator shows mixed regulation fashion. In addition, the efficiency of the regulator is also changeable. These conclusions were supported by numerous data obtained in studies of protein regulation and enzyme regulation.
Fig. 1. Distribution curves of the REC and native protein. P, probability of active conformations of an enzyme; S, value for quantifying a working condition, such as temperature, urea, or salt concentration of the buffer, pH, or pressure. Compared with naked enzyme, the distribution curve of active conformation of a REC is shifted into another position. (The distribution curve of the REC and native protein are not strictly the same in most cases.)
PROPERTIES OF ARRHENIUS EQUATION OF ENZYMATIC REACTION
Temperature is a fundamental factor that influences the activity of all species of enzymes, and a satisfactory model of enzyme regulation should give a good description for behaviors of enzymatic kinetics.
In view of experimental research, we can learn more from properties of enzymatic kinetics. In other ways, these data can be utilized to judge the profile of an active conformation curve and other properties of enzymatic kinetics (see following discussion).
The standard Arrhenius equation that describes simple kinetic properties of a chemical reaction can be expressed as:
k = Ae–ΔE/kBT,
where k is rate constant, kB is the Boltzmann constant, A is pre-exponential factor, ΔE is activation energy, and T represents absolute temperature.
According to the dynamic model for enzyme activity and partition function of protein conformation, the Arrhenius equation of an enzymatic reaction can be written as [14]:
k = APe–[ΔE0 + BT(T – T0)]kBT = APDTe–ΔE0/kBT, (1)
where P is probability of active conformation of the enzyme, T0 is reference temperature, A is pre-exponential factor at the reference temperature, ΔE0 is activation energy of the enzymatic reaction at the reference temperature, and DT is the factor arising from the thermodynamic revision of the transition state of the enzymatic reaction [14].
The mathematical analysis of an enzymatic reaction is very complex, and we have no space to discuss it here, but in view of experimental research, it could be simplified. We can take a limited range of temperature and a linear Arrhenius plot could be obtained.
Theoretically speaking, the abundance of active conformations of an enzyme increased when protein dynamics was decreased at low temperature (if a protein could be cold denatured), the abundance of active conformations was decreased when protein dynamics was increased at high temperature (reversible protein heat denaturation).
This equation indicated that the pre-exponential factor of the Arrhenius equation could be utilized to monitor a change in active conformation of enzymes. But experimental reports are few.
ENZYME REGULATION VIA INFLUENCE ON ABUNDANCE OF ACTIVE
CONFORMATIONS
The active conformation of an enzyme has been proposed in biochemistry for a long time, and its role in enzyme activity has been well-established [22]. But this concept has not been addressed as a fundamental theory for enzyme regulation because the equilibrium between inactive and active conformations cannot be described quantitatively without knowing the partition function of the conformational states of the protein [14]. Another reason is that not all experimental studies of protein regulation were done according to thermodynamic principles, so the thermodynamic mechanism of regulation cannot be obtained from such approaches directly.
The relation between enzyme activity and protein flexibility has been well recognized and has attracted much attention in the past 50 years [23-27]. Contemporary experimental methods such as CD, NMR, and fluorescence spectroscopy are valuable in measuring some types of protein conformations and their changes, but these methods cannot differentiate active and inactive conformation of enzymes [4, 23]. Thus, the abundance of active conformations of enzymes cannot be measured experimentally. Although conformation distribution curves can be theoretically deduced from stability curves of protein conformations, there is not enough data for it, and we must handle and test them in alternative ways.
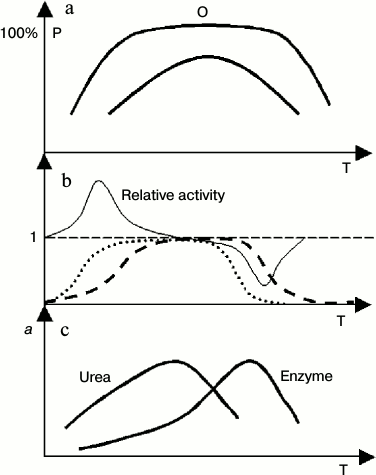
In view of protein thermodynamic structure theory, enzyme activity corresponds to one thermal system (conformation in terms of biochemistry) within a protein, and this relation could be guaranteed theoretically [13, 15]. One method to judge correctness of this opinion comes from enzyme kinetics. If the active conformation of an enzyme is changeable along temperature, the Arrhenius plot will be nonlinear. Otherwise, it will be linear. It is well known that in the range of high temperature the Arrhenius plot is nonlinear. It seems that the abundance of active conformations of some enzymes is not at 100% under normal conditions. If it is at 100%, it should satisfy several criteria: 1) the linear range of the Arrhenius plot should be large enough; 2) the plateau expressed in Figs. 2a and 2b should be observed; 3) there are no activators for this enzyme, or the working solution of the enzyme includes all types of activators; or in other words, it is at optimum conditions for enzyme activity.
Fig. 2. Cooperative behavior of temperature and urea on enzyme activity. P, abundance of active conformation; a, enzyme activity; Relative activity, ratio of enzyme activity in the presence and absence of urea; T, absolute temperature. a) General profile of distribution curves of active conformations of enzymes with different stability (high or low). There is plateau in the distribution curve of conformations of the enzyme with high stability. Within this range, the abundance of active conformations is insensitive to a change in protein dynamics or flexibility; b) ideal profile of a relative enzyme activity curve with or without urea in the working buffer, and the corresponding distribution curve of active conformations of the enzyme (with high thermal stability). The dashed and dotted lines represents distribution curves of active conformations of the enzyme in common buffer (dashed) or urea buffer. (Not all parts of this figure can be seen in all cases because cold denaturation cannot be observed for some enzymes); c) general profile of enzyme activity curve with or without urea in the working buffer for the enzymes with low thermostability.
Another type of experimental evidence for the change in abundance of active conformation of an enzyme in solution comes from cooperation or counteraction phenomena [28-31]. If the effect of a regulator or a factor cooperated with the denaturation effect of high temperature for a protein, it will favor transition from active to inactive conformation of the enzyme too, and vice versa. At low temperature, low concentrations of urea and guanidine hydrochloride enhance the active conformation stability, which increases the abundance of active conformation of enzyme and enzyme activity; at high temperature, urea and guanidine hydrochloride are cooperative with temperature in lowering the protein stability and decrease the abundance of active conformation of enzymes, which finally results in the decrease in enzyme activity. Results of a number of reports agree well with this conclusion [26, 32]. The previous opinion is that that an increase in protein flexibility at the active site of the enzyme results in a change in enzyme activity [26]. This opinion is questionable, for the change at all sites of a protein could alter the protein stability and influence abundance of active conformations of enzymes.
To gain better understanding of enzyme regulation, it is good to draw diversified properties of the enzyme and enzymatic reaction in a figure, and then their relation can be clearly expressed.
Two typical distribution curves of protein conformation are shown in Fig. 2a, one type of conformation having high thermal stability and another having low thermal stability. The tests of Pace have provided excellent evidence for this [33].
Figure 2b outlines the general profile of cooperation of urea and temperature on the activity of an enzyme that has high thermal stability. The cooperation between urea and temperature is obviously in the range of low or high temperature. In the middle range of temperature, although cooperation to increase protein dynamics between urea and temperature occurs, it does not affect the abundance of active conformation of enzymes, and it has little or no impact on the enzyme activity.
If the thermal stability of active conformation of an enzyme is low, the cooperative effect of urea and temperature on enzyme activity show another form (Fig. 2c). Due to cooperation of high temperature and urea on protein denaturation, the optimum temperature of enzymatic reaction has been shifted into low temperature in the presence of urea.
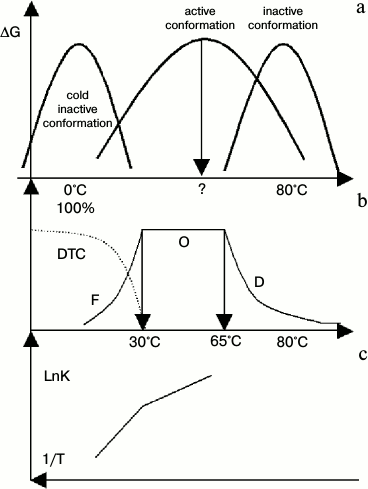
According to Eq. (1), the change in abundance of active conformations in a range of experimental temperature could be reflected in the pre-exponential factor of the Arrhenius equation. This is true for thermophilic alcohol dehydrogenase isolated from Bacillus stearothermophilus (htADH) [34]. It has been observed that the pre-exponential factor is as high as 1025.2, an unbelievable value for a chemical reaction in conventional view of chemistry. The authors of that paper [34] guessed a mechanism similar to our conclusion proposed in this paper. Its behaviors were shown in Fig. 3a. At low temperature, subunits of htADH dissociate and the enzyme loses its activity (cold denaturation). At high temperature, it also denatures. As there is no system studying it, we drew it by general profile of stability curve and some properties of htADH that match Fig. 3b well. Figure 3b illustrates the distribution curve of three conformations. (At low temperature, htADH is not stable thermodynamically and it will denature slowly. But in the range of times used in tests, it shows inactive conformations or dynamic trapped conformation, DTC). Figure 3c is the Arrhenius plot of the enzymatic reaction.
Fig. 3. Diagram of diversified properties of htADH. DTC represents dynamic trapped conformation at low temperature. a) Stability curves of three types of conformations of htADH. (It was drawn according to the general profile of the stability curve of a protein, protein denaturation, and several points of enzymatic reaction. It matches Figs. 3b and 3c well); b) distribution curve of active conformation of htADH. In range F, the abundance of active conformations of the enzyme increase as temperature increases. In range O, the abundance of active conformations remains constant (100%). In range D, the abundance of active conformation decreases as temperature increases. A change in protein dynamics has opposite effect on enzyme activity in ranges F and D; c) Arrhenius plot of the enzymatic reaction. (The coordinate is changed to an uncommon expression to match up Figs. 3a and 3b.)
In Fig. 3, we show that at low temperature the abundance of active conformations increases as temperature increases, thus resulting in a break in the Arrhenius plot at its boundary. In area O, the abundance of active conformations remains unchanged. In area D, the abundance of active conformations decreases as temperature increases. A mutation in its gene can influence the thermal state of a protein product, and it can alter the break temperature [34]. This figure clearly shows that the regulation of abundance of active conformations is an efficient way for enzyme regulation.
ENZYME REGULATION VIA THERMAL STATE OF ACTIVE
CONFORMATIONS
Theoretically speaking, the change in abundance of active conformations of an enzyme in solution can provide an explanation for numerous data and phenomena related to enzyme regulation. But one problem must be addressed: the energy level of active conformations of enzymes is changeable under different conditions – does this have an effect on enzyme regulation? The answer is yes. In Eq. (1), DT represents the dynamic contribution of active conformation to enzyme activity. From Eq. (1), we can also learn that this mechanism for enzyme regulation is not suitable for physiological regulation of enzyme as it is not sufficiently sensitive to stimulus.
In the view of structural biology, different energy levels of active conformations of an enzyme can be recognized as different conformations. In practice, it is very difficult to distinguish active conformations of an enzyme and the transition state of an enzymatic reaction, so here we discus general properties of both. The state of active conformations can be judged by many criteria, such as Kcat, KIE (kinetic isotope effect), Km, and Kcat/Km [35].
Thermal states of active conformations are changeable. This conclusion is supported by facts: 1) different subunits of hemoglobin, even the monomer, can bind to oxygen with different affinity [1]; 2) an enzyme may show negative and positive cooperation under different conditions, so the thermal state of enzymes under different conditions must be different [36, 37]; 3) the maximal rate of an enzymatic reaction, or Kcat, is not constant, and the product of each various gene mutation has its particular value; 4) KIE for enzymatic reactions are changeable under different conditions [38]; 5) it has been suggested that dissociation of protein oligomers acts as a mechanism of enzyme regulation [39].
Thermal states of active conformations are substrate dependent. When sucAAPF-SBzl (succinyl-AAPF-thiosulfobenzoate) was used as substrate, the Kcat of trypsin, mutant trypsin D189S, and chymotrypsin-like trypsin (Tr-chy, +S1+L1+L2) were similar. This indicates that the transition states of these enzymatic reactions are similar. But when sucAAPF-pNA (succinyl-AAPF-para-nitroanilide) was used as substrate, their Kcat values were dramatically different from each other [40, 41]. Another kind of evidence is that promiscuity of enzymatic reaction could be found under extreme conditions [42].
Thermal states of active conformations are dependent on global conformation. From studying of conversion from trypsin to chymotrypsin, it was found that the surface loop far from the active site of the enzyme plays a key role in the enzyme conversion [40].
Although this mechanism is of great importance in theoretical science and enzymology, it is not the basic mechanism for enzyme regulation. In most cases, thermal state changes in active conformations of enzymes occur under extreme conditions far from the physiological environment, and their biological significance remains to be demonstrated in the future.
IS MIXED COOPERATION COMMON IN ENZYME REGULATION?
In view of experimental science, the mechanism of enzyme regulation was established on the concept of cooperation in enzymatic kinetics. However, cooperation is a deduced concept within our model. Theoretically speaking, the substrate that binds first to a subunit of an oligomeric enzyme could be considered a regulator of other subunits, and it can either enhance (positive cooperation) or decrease (negative cooperation) the binding affinity between substrate and another subunit of the enzyme under different conditions. Thus, we conclude that the mixed cooperation phenomenon, an enzyme showing positive cooperative behavior under certain conditions and negative cooperative behavior under other conditions, is common in enzymology.
A large number of enzymes that show positive cooperative behavior have been reported, and the number of enzymes that show negative cooperative behavior is small. There are only a few reports about mixed cooperative kinetics in enzymology [37]. How can we reconcile such different opinions? One possible answer is that studies on enzymatic reactions are generally processed under conditions near the physiological environment, and mixed cooperative behavior cannot be observed because it occurs under conditions far from the physiological environment.
Hemoglobin is a model enzyme in our study of kinetic cooperativity. It shows positive cooperative behavior under normal conditions, and the Hill coefficient is changeable under different conditions. However, there is no report that it can show negative cooperative behavior [43-46]. After examining conditions under which the experimental tests were done, we found that the behavior of binding between oxygen and hemoglobin under extreme conditions has not been explored. We predicted that negative cooperative binding between hemoglobin and oxygen should appear under extreme conditions such as low or high temperature, low or high salt concentration, or low or high pH of the medium. Even though negative cooperation of oxygen binding by hemoglobin has not been found under such conditions, it might appear in a mutant of hemoglobin.
CONCLUSION AND PERSPECTIVE
This paper shows that enzyme regulation can and must be explained by the laws of thermodynamics, and our model has many advantages over the allosteric regulation mechanism. First, our model reveals a thermodynamic mechanism for enzyme regulation that cannot be provided by an allosteric model. Second, there is difficulty within the allosteric model to give a satisfactory explanation for negative cooperativity, and within our model both negative and positive regulatory behaviors of an enzyme can be shown under different conditions. Third, within our model enzyme activity, enzyme regulation, and bioinformation integration (cooperation or counteraction) within an enzyme molecule are processed via a common mechanism – thermodynamic reorganization of the protein – while the allosteric model cannot support such view. Fourth, within our model all enzymes, oligomeric and monomeric, are regulatory, while an allosteric model cannot explain regulatory behaviors of monomeric enzymes. Fifth, the effect of protein dynamics on enzyme regulation is well defined in our model. Sixth, conformation change of an enzyme is not essential within our model, and it is an absolute perquisite within an allosteric regulation mechanism [7]. Seventh, our model can give a quantitative description of enzyme activity and regulation, while the allosteric model cannot. Finally, within our model, there are many allodynamic sites for an enzyme, but the allosteric site is not an essential concept for some factors, such as urea, that can exert their effect on nearly all sites of a protein.
However, there is no systematic and experimental study about our model, and therefore further study on a model enzyme should be done in the future. The following direction should be given particular attention in future studies.
1. The pre-exponential factor of the Arrhenius equation and activation energy of the enzymatic reaction should be studied simultaneously.
2. The active conformation distribution curve and stability curve of the enzyme should be experimentally studied.
3. The thermodynamic parameters of enzymatic reaction with different substrates should be measured over wide ranges, and particularly this should be done under unfavorable conditions for enzymatic reaction.
4. The rate of protein conformational change and enzyme activity should be addressed in the future.
5. Information integration on protein stability and active conformation stability (function) should be stressed in future studies.
The author thanks Professor V. Matveev (Institute of Cytology, Russian Academy of Sciences, Saint Petersburg, Russia) and Dr. Zhenbao Yu (Lady Davis Institute for Medical Research and Departments of Oncology and Medicine, McGill University, Canada) for their valuable suggestions regarding this work.
REFERENCES
1.Hill, A. V. (1910) The possible effects of the
aggregation of the molecules of hemoglobin on the dissociation curves,
J. Physiol., 40, iv-vii.
2.Koshland, D. E., Nemethy, G., and Filmer, D. (1966)
Comparison of experimental binding data and theoretical models in
proteins containing subunits, Biochemistry, 5,
365-385.
3.Monod, J., Wyman, J., and Changeux, J. P. (1965).
On the nature of allosteric transitions—a plausible model, J.
Mol. Biol., 12, 88-118.
4.Tzeng, S. R., and Kalodimos, C. G. (2011) Protein
dynamics and allostery: an NMR view, Curr. Opin. Struct. Biol.,
21, 62-67.
5.Tsai, C. J., Del Sol, A., and Nussinov, R. (2008)
Allostery: absence of a change in shape does not imply that allostery
is not at play, J. Mol. Biol., 378, 1-11.
6.Wand, A. J. (2001) Dynamic activation of protein
function: a view emerging from NMR spectroscopy, Nat. Struct.
Biol., 8, 926-931.
7.Cooper, A., and Dryden, D. T. (1984) Allostery
without conformational change. A plausible model, Eur. Biophys.
J., 11, 103-109.
8.Goodey, N., and Benkovic, S. (2008) Allosteric
regulation and catalysis emerge via a common route, Nat. Chem.
Biol., 4, 474-482.
9.Taylor, S. S., and Kornev, A. P. (2011) Protein
kinases: evolution of dynamic regulatory proteins, Trends Biochem.
Sci., 36, 65-77.
10.Motlagh, H. N., and Hilser, V. J. (2012)
Agonism/antagonism switching in allosteric ensembles, Proc. Natl.
Acad. Sci. USA, 109, 4134-4139.
11.Zhao, Q. (2013) Nature of protein thermodynamics
and thermodynamics, Rev. Theor. Sci., 1, 83-101.
12.Zhao, Q. (2009) Protein thermodynamic structure,
IUBMB Life, 61, 600-606.
13.Zhao, Q. (2013) A molecular and biophysical model
of the biosignal, Quantum Matter, 2, 9-16.
14.Zhao, Q. (2012) Partition function of protein
conformational state, J. Comput. Theor. Nanosci., 9,
745-751.
15.Zhao, Q. (2011) Dynamic model of enzymes action,
Protein Pept. Lett., 18, 92-99.
16.Zhao, Q. (2013) Allodynamic regulation of protein
activity, Quantum Matter, 2, 144-152.
17.Lonhienne, T., Gerday, C., and Feller, G. (2000)
Psychrophilic enzymes: revisiting the thermodynamic parameters of
activation may explain local flexibility, Biochim. Biophys.
Acta, 1543, 1-10.
18.Pace, C. N., Grimsley, G. R., Thomson, J. A., and
Barnett, B. J. (1988) Conformational stability and activity of
ribonuclease T1 with zero, one, and two intact disulfide bonds, J.
Biol. Chem., 263, 11820-11825.
19.Ramsey, I. S., Delling, M., and Clapham, D. E.
(2006) An introduction to TRP channels, Annu. Rev. Physiol.,
68, 619-647.
20.Inouye, K., Kuzuya, K., and Tonomura, B. I.
(1998) Sodium chloride enhances markedly the thermal stability of
thermolysin as well as its catalytic activity, Biochim. Biophys.
Acta, 1388, 209-214.
21.Kanade, S., Paul, B., Rao, A., and Gowda, L.
(2006) The conformational state of polyphenol oxidase from field bean
(Dolichos lablab) upon SDS and acid-pH activation, Biochem. J.,
395, 551-562.
22.Fersht, A. (1985) Enzyme Structure and
Mechanism, Freeman Press, San Francisco.
23.Pace, C. N., Vajdos, F., Fee, L., Grimsley, G.,
and Gray, T. (1995) How to measure and predict the molar absorption
coefficient of a protein, Protein Sci., 4, 2411-2423.
24.Bahar, I., Atilgan, A. R., Demirel, M. C., and
Erman, B. (1998) Vibrational dynamics of folded proteins: significance
of slow and fast motions in relation to function and stability,
Phys. Rev. Lett., 80, 2733-2736.
25.Zavodszky, P., Kardos, J., Svingor, A., and
Petsko, G. A. (1998) Adjustment of conformational flexibility is a key
event in the thermal adaptation of proteins, Proc. Natl. Acad. Sci.
USA, 95, 7406-7411.
26.Tsou, C. L. (1998) The role of active site
flexibility in enzyme catalysis, Biochemistry (Moscow),
63, 253-258.
27.Daniel, R. M., and Danson, M. J. (2013)
Temperature and the catalytic activity of enzymes: a fresh
understanding, FEBS Lett., 587, 2738-2743.
28.Mayr, L. M., and Schmid, F. X. (1993)
Stabilization of a protein by guanidinium chloride,
Biochemistry, 32, 7994-7998.
29.Bhuyan, A. K. (2002) Protein stabilization by
urea and guanidine hydrochloride, Biochemistry, 41,
13386-13394.
30.Yancey, P. H., and Somero, G. N. (1979)
Counteraction of urea destabilization of protein structure by
methylamine osmoregulatory compounds of elasmobranch fishes,
Biochem. J., 183, 317-323.
31.Baldwin, R. L. (1996) How Hofmeister ion
interactions affect protein stability, Biophys. J., 71,
2056-2063.
32.Zoldak, G., Sutak, R., Antalik, M., Sprinzl, M.,
and Sedlak, E. (2003) Role of conformational flexibility for enzymatic
activity in NADH oxidase from Thermus thermophiles, Eur. J.
Biochem., 270, 4887-4897.
33.Pace, C. N., and Tanford, C. (1968)
Thermodynamics of the unfolding of β-lactoglobulin A in aqueous
urea solutions between 5 and 55, Biochemistry, 7,
198-208.
34.Nagel, Z. D., Dong, M., Bahnson, B. J., and
Klinman, J. P. (2011) Impaired protein conformational landscapes as
revealed in anomalous Arrhenius prefactors, Proc. Natl. Acad. Sci.
USA, 108, 10520-10525.
35.Schramm, V. L. (1998) Enzymatic transition states
and transition state analog design, Annu. Rev. Biochem.,
67, 693-720.
36.Robert, C. A., and Koshland, D. E. (1970)
Positive and negative cooperativity in yeast glyceraldehyde 3-phosphate
dehydrogenase, Biochemistry, 9, 3337-3342.
37.Koshland, D. E., and Hamadani, K. (2002)
Proteomics and models for enzyme cooperativity, J. Biol. Chem.,
277, 46841-46844.
38.Kohen, A., Cannio, R., Bartolucci, S., and
Klinman, J. P. (1999) Enzyme dynamics and hydrogen tunneling in a
thermophilic alcohol dehydrogenase, Nature, 399,
496-499.
39.Traut, T. W. (1994) Dissociation of enzyme
oligomers: a mechanism for allosteric regulation, Crit. Rev.
Biochem. Mol. Biol., 29, 125-163.
40.Hedstrom, L., Szilagyi, L., and Rutter, W. J.
(1992) Converting trypsin to chymotrypsin: the role of surface loops,
Science, 255, 1249-1253.
41.Hedstrom, L. (2002) Serine protease mechanism and
specificity, Chem. Rev., 102, 4501-4524.
42.Khersonsky, O., and Tawfik, D. S. (2010) Enzyme
promiscuity: a mechanistic and evolutionary perspective, Annu. Rev.
Biochem., 79, 471-505.
43.Ogata, R. T., and McConnell, H. M. (1972)
Mechanism of cooperative oxygen binding to hemoglobin, Proc. Natl.
Acad. Sci. USA, 69, 335-339.
44.Bruno, S., Bonaccio, M., Bettati, S., Rivetti,
C., Viappiani, C., Abbruzzetti, S., and Mozzarelli, A. (2001) High and
low oxygen affinity conformations of T state hemoglobin, Protein
Sci., 10, 2401-2407.
45.Hewitt, J. A., Kilmartin, J. V., Ten Eyck, L. F.,
and Perutz, M. F. (1972) Noncooperativity of the αβ dimer in
the reaction of hemoglobin with oxygen, Proc. Natl. Acad. Sci.
USA, 69, 203-207.
46.Gibson, Q. H. (1970) The reaction of oxygen with
hemoglobin and the kinetic basis of the effect of salt on binding of
oxygen, J. Biol. Chem., 245, 3285-3288.