Contribution of Quantitative Methods of Estimating Mortality Dynamics to Explaining Mechanisms of Aging
G. A. Shilovsky1,2,3*, T. S. Putyatina3, A. V. Markov3, and V. P. Skulachev1,2
1Belozersky Institute of Physico-Chemical Biology, Lomonosov Moscow State University, 119991 Moscow, Russia; E-mail: grgerontol@gmail.com2Lomonosov Moscow State University, Faculty of Bioengineering and Bioinformatics, 119991 Moscow, Russia
3Lomonosov Moscow State University, Faculty of Biology, 119991 Moscow, Russia
* To whom correspondence should be addressed.
Received August 7, 2015; Revision received September 6, 2015
Accumulation of various types of unrepaired damage of the genome because of increasing production of reactive oxygen species and decreasing efficiency of the antioxidant defense system and repair systems can cause age-related diseases and emergence of phenotypic signs of senescence. This should lead to increasing vulnerability and to mortality monotonously increasing with age independently of the position of the species on the evolutionary tree. In this light, the survival, mortality, and fertility curves for 45 animal and plant species and one alga published by the Max Planck Institute for Demographic Research (Germany/Denmark) are of special interest (Jones, O. R., et al. (2014) Nature, 505, 169-173). We divided all species treated in that study into four groups according to the ratio of mortality at the terminal age (which corresponds to 5% survival) and average mortality during the entire studied period. For animals of group IV (long-lived and senescent), including humans, the Jones method makes it possible to trace mortality during the entire life cycle. The same applies to short-lived animals (e.g. nematodes or the tundra vole), whether they display the Gompertz type of senescence or not. However, in long-lived species with a less pronounced increase in mortality with age (e.g. the freshwater crocodile, hermit crab, or Scots pine), as well as in animals of average lifespan that reach the terminal age earlier than they could have enough time to become senescent, the Jones method is capable of characterizing only a small part of the life cycle and does not allow judging how senescence manifests itself at late stages of the life cycle. Thus, it is known that old trees display signs of biological senescence rather clearly; although Jones et al. consider them non-senescent organisms because less than 5% of sexually mature individuals survive to display the first manifestations of these characters. We have concluded that the classification proposed by Jones et al. makes it possible to approximately divide animals and plants only by their levels of the Gompertz type of senescence (i.e. actuarial senescence), whereas susceptibility to biological senescence can be estimated only when principally different models are applied.
KEY WORDS: lifespan, senescence, non-senescent species, survival curves, phenoptosisDOI: 10.1134/S0006297915120020
Abbreviations: LS, lifespan; ROS, reactive oxygen species.
The purpose of this study was to review and critically assess studies
that investigate the process of senescence and its evolution and to
compare the main patterns of aging in representatives of different
lineages.
There are two main historically developed approaches to the study of aging. The first approach is focused on the search for mechanisms and molecular “substrates” of senescence. It deals above all with the accumulation of DNA damage caused by exogenous and endogenously generated radicals [1-5]. The accumulation of DNA damage and decreasing ability of cells to repair this damage and respond to it as the organism ages should lead to poorer functioning of particular cells, tissues, organs, and the entire organism (eventually leading to higher chances of its death). A living cell produces reactive oxygen species (ROS), which damage various macromolecules, including DNA, affecting cellular functions and, possibly, the development of age-related changes [2, 6-11]. The ability of the organism to neutralize the ROS produced can be an important factor in determining individual and species-specific lifespan (LS) [12]. Therefore, animals that have greater LS should, ceteris paribus, have a better ability to respond to ROS and to DNA damage caused by ROS. This conclusion is confirmed, among other things, by the positive correlation between the activity of systems involved in DNA repair and maximum LS in mammals [13-16].
The second main approach, which started in the 19th century from the work of Gompertz, a mathematician specialized in life insurance, has also become quite widespread [15, 17-24].
Gompertz showed that humans display senescence, which he defined as increasing probability of death with age. It turned out that if human life is divided into a number of equal intervals, the probability of death (the ratio of the number of those who die during each interval and those who survived to its beginning) inevitably grows with age (“the law of mortality”) [22].
Survival tables and curves were later made and analyzed for many other animals (Tables 1-3). It turned out that absence of senescence (the Gompertz type of senescence) does not necessarily lead to long LS (see below), i.e. a cohort that successfully stands against the tendency of increasing probability of death with age does not necessarily function longer than other cohorts do. It was found that those species in which the probability of death does not increase with age could nevertheless display signs of biological senescence, i.e. decline of physiological functions and accumulation of some degenerative changes (which are not lethal per se). Finch proposed two criteria of negligibly slow aging: absence of increase in mortality and negligibly small functional degradations with age [25].
Table 1. Age-related dynamics of fertility
and mortality in plants and algae
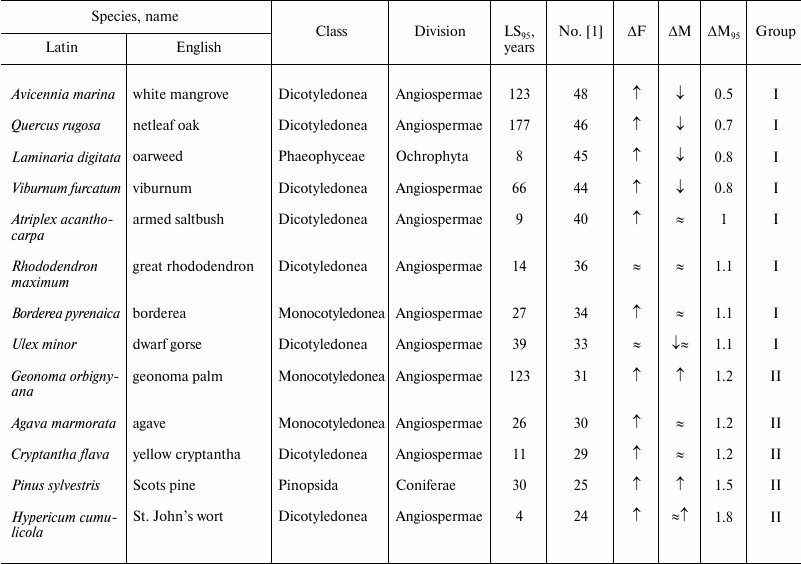
Note: ↑, increasing; ↓, decreasing; ≈,
constant; ΔF, change of fertility with age;
ΔM, change of mortality with age; LS95,
cohort age of 5% survival; ΔM95, ratio of
mortality at the terminal age (LS95) and average mortality.
The data are grouped in decreasing order of mortality (decreasing
number according to Jones et al. [1]).
Table 2. Age-related dynamics of fertility
and mortality in vertebrates
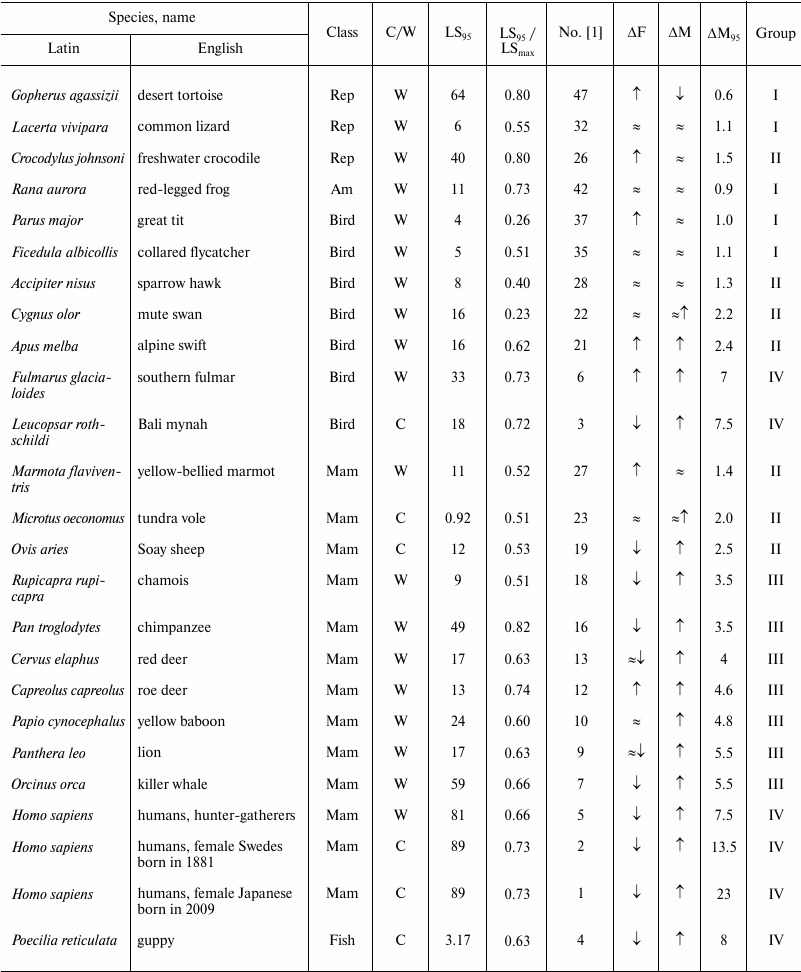
Note: Mam, mammals; Rep, reptiles; Am, amphibians;
↑, increasing; ↓, decreasing; ≈,
constant; C, observed in captivity; W, observed in wild;
LSmax, maximum LS; ΔF, change of
fertility with age; ΔM, change of mortality with age;
LS95, cohort age of 5% survival;
ΔM95, ratio of mortality at the terminal age
(LS95) and average mortality. The data within each class are
grouped in decreasing order of mortality (decreasing number according
to Jones et al. [1]).
Table 3. Age-related dynamics of fertility
and mortality in invertebrates
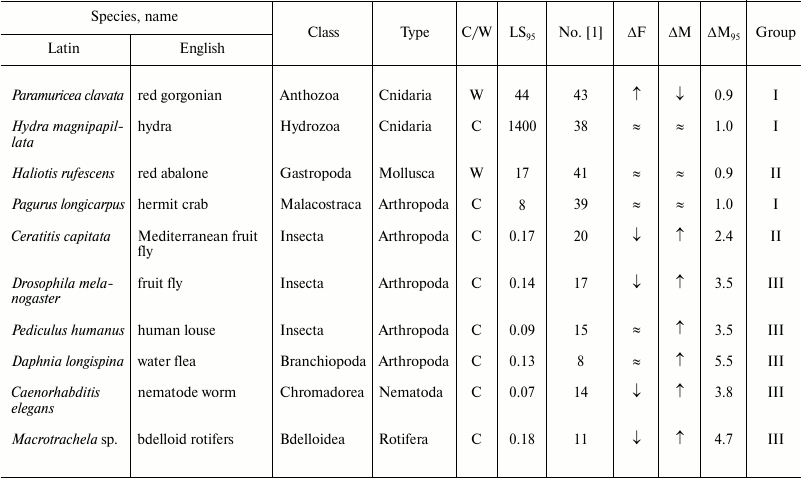
Note: ↑, increasing; ↓, decreasing; ≈, constant;
C, observed in captivity; W, observed in wild;
LS95, cohort age of 5% survival; ΔF,
change of fertility with age; ΔM, change of mortality with
age; ΔM95, ratio of mortality at the terminal
age (LS95) and average mortality. The data within each
phylum are grouped in decreasing order of mortality (decreasing number
according to Jones et al. [1]).
Many theories have been proposed to explain the emergence of the phenomenon of senescence and its changes in the course of evolution [2, 23, 26-31].
Weismann was the first to suggest that since non-senescent individuals are bad for the population, because they occupy the place of younger ones, evolution should produce a senescence program aimed at purging the population from aged individuals [26]. He believed that the biological mechanism of senescence was based on the limited number of divisions of somatic cells (in contrast to the unlimited proliferation of sex cells) and explained interspecies differences in LS in animals by the numbers of cell generations.
However, the existing theoretical approaches provide no complete explanation of the fact that senescence has evolved in some species, but not in others [32], and that even relatively closely related species sometimes display quite considerable differences in LS: (i) vertebrates: mammals: naked mole rat (Heterocephalus glaber), 32 years, and house mouse (Mus musculus), 3 years; birds: eagle owl (Bubo bubo), 68 years, and elf owl (Micrathene whitneyi), 6 years; raven (Corvus corax), 69 years, and hooded crow (Corvus cornix), 17 years; reptiles: giant tortoise (Testudo gigantea), 180 years, and panther chameleon (Chamaeleo pardalis), 2 years; amphibians: Japanese giant salamander (Megalobatrachus japonicus), 65 years, olm (Proteus anguinus), 68 years, and blue-legged mantella (Mantella expectata), 3 years; (ii) invertebrates: mollusks: freshwater pearl mussel (Margaritana margaritifera), 100 years, and bay scallop (Argopecten irradians), 2 years; (iii) echinoderms: red sea urchin (Strongylocentrotus franciscanus), 60 years, West Indian sea egg (Tripneustes ventricosus), 3 years, mosaic sea star (Plectaster decanus), 60 years, and sea cucumber (Isostichopus badionotus), 5 years; (iv) nematodes: a parasitic nematode (Loa loa), 15 years, and a free-living nematode (Caenorhabditis elegans), 0.017 year [23, 33-37].
Since LS as a species-specific character is as stable as body size or fecundity, it can be assumed that LS (i.e. the moment of death) and its mechanisms should be at least partly programmed in the genome. The suggestion about programmed death of the organism, put forward by Weismann more than a century ago, can be fairly appreciated only now, when the phenomena of self-liquidation have been described for cells and separately for mitochondria, making it possible to propose the new theory of programmed death [38, 39]. According to modern notions, programmed death of an organism, i.e. death caused by triggering the start of the genetic program of self-liquidation of the individual, is a real phenomenon. Such regulation of LS should be distinguished from purely chemical aging, not programmed in the genome. One example of chemical aging is the L→D-isomerization of amino acids in crystallins, proteins of the eye lens, in whales. Because of this spontaneous process, in 200-year-old whales about 40% of L-aspartate in crystallins turns into the D-isomer, presumably having a negative effect on the properties of this protein, which, once formed in the lens, is retained there for the entire life. Other examples of non-programmed, chemical aging include the processes of carbonylation and deamidation of proteins [11, 40].
Thus, Weismann’s theory of senescence as an adaptive mechanism of programmed death can be combined with the alternative view that senescence is a result of accumulation of damage and mistakes. Accumulation of damage could be traced by special systems that send a lethal signal to activate the phenoptosis program (programmed death of the organism) when the damage reaches some critical level. This program is adjusted to eliminate the damaged object before it makes the existence of the organism (or another living system) impossible. Such a mechanism is aimed at preventing the emergence of asocial monsters that can destroy the community and the entire population. This is how the “Samurai” law of biology manifests itself: “It is better to die than to make a mistake”. This system is responsible for the following functions: (i) prevention of oxidation-related or any other damage to the genome, (ii) repair of damaged genome, and (iii) purging living systems of potential monsters with damaged genomes. One example of pathology that displays features of phenoptosis is septic shock. Many of its features indicate that its rapid lethal effect is specially organized by the organism itself after it becomes subject to a large-scale bacterial invasion. It prevents the development of an epidemic. Sepsis is accompanied by large-scale release of cytokines by macrophages, which induces apoptosis [11, 41].
As a rule, phenoptosis is encoded in the genome and consists of a chain of biochemical events that ultimately result in self-destruction of the organism. Less often, such death results from a behavioral reaction encoded in the genome of the organism’s sexual partner [40, 42-46].
Worsening environmental conditions, like any other deviation of the system from the optimum, should weaken the defenses of the organism and thus increase the probability of mutations and accumulation of damage, which, in turn, stimulates phenoptosis. This probability increases also as fecundity increases and alteration of generations accelerates, i.e. as LS decreases. For instance, in some killifish species of the genus Nothobranchius, LS varies by a factor of up to five, depending on the natural habitat occupied by the species [47]. Austad provides an example of average LS increasing and senescence (determined from the structure of collagen in tendons of the tail) decreasing in a population of opossums that accidentally colonized a small isolated island and ended up under conditions of weakened selection pressure compared to continental populations for lack of predators [15, 48].
Rapid phenoptosis is often associated with reproduction. In such cases, mating includes a behavioral or biochemical suicidal program. In squids, the male tears the skin of the female, injects a spermatophore, and immediately dies after mating; the female dies after laying a clutch of eggs [49]. Salmonid fish of the genus Oncorhynchus become senescent and die one or two months after spawning, not because of exhaustion of the organism, but because of triggering a special program in which the key role is played by steroid hormones of the adrenal glands. Lampreys and eels, like salmonids, die soon after breeding [41]. In lampreys, life can be prolonged by removal of gonads or the pituitary gland; in eels, it can be prolonged by prevention of mating. Such death is also known among mammals, e.g. Australian marsupials of the genus Antechinus, in which males commit biochemical suicide immediately after the breeding season [50]. In some animals, the very structure of the body is incompatible with life of any considerable length, e.g. adult mayflies are unable to eat for lack of mouthparts and die of hunger soon after mating [11].
Bamboo lives for 10 to 15 years with vegetative reproduction and then blossoms and dies after ripening of the seeds. Arabidopsis with two genes knocked out grows almost normally, blossoms, and bears fruit more poorly, but it has LS longer by at least an order of magnitude; it has thicker stem and leaves and additional rosettes of leaves [51, 52]. In the Mexican agave, which usually lives for ten years, annual removal of the flowering shoot increases LS by a factor of ten. Rapid senescence and death of soy can be prevented by removal of fruits or seeds ripening inside them [53, 54]. It can be suggested that phenoptosis exists in any species that breed only once.
Senile phenoptosis could appear as sudden death, which happens when the individual reaches some critical age. Bowles mentions one species of marine birds that suddenly die when they are about 50 years old, showing no signs of senescence [55].
Usually, however, death from old age is the result of a very prolonged process (slow phenoptosis). However, in case of individuals with multiple reproduction it can prove more beneficial for the species than rapid apoptosis: the presence of a beneficial character in an individual can for some time compensate adverse effects of senescence, thus giving the individual advantages in breeding. Phenoptosis in natural environments is beneficial above all for survival and evolution of communities under aggressive conditions. A considerable role in this process is played by epigenetic modifications of chromatin [56, 57]. In contrast to situations treated by mutation accumulation and disposable soma theories, which assume constant pressure of adverse environmental conditions (predators or diseases), such a program could have evolved for adaptation to short-term extreme external influences (fluctuations of temperature or humidity of the environment or of levels of food resources) [58, 59].
Analysis of mortality curves. Scientists of the Max Planck Research Group on Modeling the Evolution of Aging (Rostock, Germany, and Odense, Denmark), headed by A. Baudisch, studied mortality and fecundity curves [1].
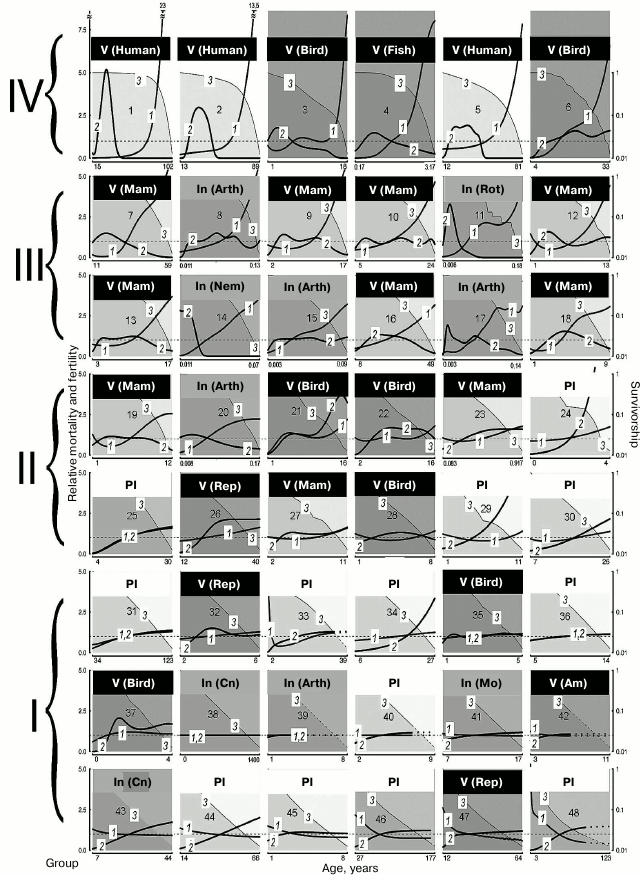
Analysis of functional changes (in fecundity, mobility, and memory) that happen during senescence shows that different organs and tissues undergo age-related disturbances at different rates. In addition, LS varies from individual to individual. Even genetically similar or identical individuals (e.g. workers and queens of social insects) can have fundamentally different LS trajectories. Contrary to the opinion that evolution should inevitably lead to mortality increasing and fertility decreasing with age after maturation, considerable differences between species have been shown in the dynamics of these parameters (increasing, stable, decreasing, convex, or concave mortality curves) in both long-lived and short-lived species (figure) [1].
Demographic trajectories according to Jones et al. [1] (modified, reproduced by the courtesy of the NPG group). The relative mortality (curve 1) and fertility (curve 2) are shown as functions of age, from the moment of maturity to the age at which only 5% of adults survive; mortality and fertility are normalized relative to average values (calculated for all living adults from maturity to terminal age) (curve 1, axis Y to the left). The dashed lines are trajectories obtained by mathematical calculations. Mortality and fertility averaged for all ages are shown with horizontal dashed gray lines. Survivorship (ratio of the size of the cohort still alive at this age and the number of surviving individuals by the moment of sexual maturity) (curve 3, axis Y to the right) is represented in logarithmic scale. The graphs are numbered from 1 to 48 in decreasing order of relative mortality by the terminal age from the highest level of relative mortality at the terminal age (top left) to the lowest level (bottom right), and they are arranged sequentially, row by row and left to right. The dimension of axis X (age) is given in years. 1) Humans, female Japanese born in 2009 (Homo sapiens); 2) humans, female Swedes born in 1881 (Homo sapiens); 3) Bali mynah (Leucopsar rothschildi); 4) guppy (Poecilia reticulata); 5) humans, hunter-gatherers (Homo sapiens); 6) southern fulmar (Fulmarus glacialoides); 7) killer whale (Orcinus orca); 8) water flea (Daphnia longispina); 9) lion (Panthera leo); 10) yellow baboon (Papio cynocephalus); 11) bdelloid rotifers (Macrotrachela sp.); 12) roe deer (Capreolus capreolus); 13) red deer (Cervus elaphus); 14) nematode worm (Caenorhabditis elegans); 15) human louse (Pediculus humanus); 16) chimpanzee (Pan troglodytes); 17) fruit fly (Drosophila melanogaster); 18) chamois (Rupicapra rupicapra); 19) Soay sheep (Ovis aries); 20) Mediterranean fruit fly (Ceratitis capitata); 21) alpine swift (Apus melba); 22) mute swan (Cygnus olor); 23) tundra vole (Microtus oeconomus); 24) St. John’s wort (Hypericum cumulicola); 25) Scots pine (Pinus sylvestris); 26) freshwater crocodile (Crocodylus johnsoni); 27) yellow-bellied marmot (Marmota flaviventris); 28) sparrow hawk (Accipiter nisus); 29) yellow cryptantha (Cryptantha flava); 30) agave (Agave marmorata); 31) geonoma palm (Geonoma orbignyana); 32) common lizard (Lacerta vivipara); 33) dwarf gorse (Ulex minor); 34) borderea (Borderea pyrenaica); 35) collared flycatcher (Ficedula albicollis); 36) great rhododendron (Rhododendron maximum); 37) great tit (Parus major); 38) hydra (Hydra magnipapillata); 39) hermit crab (Pagurus longicarpus); 40) armed saltbush (Atriplex acanthocarpa); 41) red abalone (Haliotis rufescens); 42) red-legged frog (Rana aurora); 43) red gorgonian (Paramuricea clavata); 44) viburnum (Viburnum furcatum); 45) oarweed (Laminaria digitata); 46) netleaf oak (Quercus rugosa); 47) desert tortoise (Gopherus agassizii); 48) white mangrove (Avicennia marina). Designations: Am, amphibians; Arth, arthropods; Cn, cnidarians; In, invertebrates; Mam, mammals; Mo, mollusks; Nem, nematodes; Pl, plants; Rep, reptiles; Rot, rotifers; V, vertebrates
Vaupel has shown that in some species (those with the so-called negative senescence, group I) (figure, lower row, and Tables 2 and 3), such as the desert tortoise (Gopherus agassizii), fertility continues to increase and probability of death decreases with age after maturation [1, 60]. In other cases, initial decrease is followed by a long period of constant mortality level (e.g. in Mexican oak, Quercus rugosa), while in most species mortality increases. This variability of curves is not predicted by standard evolutionary theories of aging, which assume that mortality only increases and fertility only decreases with age [27, 28, 61-63], but do not explain differences in the scale of these changes.
Survival curves. Survival curves (concave, linear, and convex) are known among biologists [64, 65], but they were usually drawn for LS beginning with birth rather than beginning with sexual maturity as in the study discussed here [1]. Similar survival curves can be found in species that strongly differ in LS. Thus, lions and chimpanzees are close to animals with rapid life cycles, such as louse (Pediculus humanus), daphnia (Daphnia longispina), or fruit fly (Drosophila melanogaster) [1].
After the terminal age, sample size is usually rather small, and identification of age is often problematic.
Baudisch supposes that the shape of the curve is a more informative parameter for the study of aging than the rate of mortality increase [32, 66].
METHODS OF INVESTIGATION
To compare the principal patterns of the senescence process in organisms that represent different evolutionary lineages, we sorted the data of Jones et al. [1] into groups according to the mortality at the terminal age and average mortality. We numbered all species treated as they were numbered in that study (from 1 to 48, in decreasing order of the above-mentioned parameter) and divided them into four large groups, group I comprising species with the smallest changes in mortality with age, and group IV comprising species with the greatest changes in mortality with age. Jones et al. [1] provided normalized mortality and fertility curves for a broad range of taxa (11 mammals, 12 other vertebrates, 10 invertebrates including five arthropods, two cnidarians, one mollusk, one nematode, and one rotifer, 12 vascular plants, and one brown alga). For arthropods, we calculated the ratio of the LS until the moment by which only 5% of the cohort survives (LS95) and the maximum LS to reveal how well LS95 characterizes the life cycle of each species (the data are given in Table 2). The data on other species are unfortunately incomplete and contradictory, and the table value of the maximum LS was often lower than LS95 given by Jones (see, e.g. [23]). The values of maximum LS (unless specified otherwise) are taken from the database of the Max Planck Research Group on Modeling the Evolution of Aging (Rostock, Germany, and Odense, Denmark) [35]. We also indicated in the Table 2 whether the animals were observed in natural environments or in captivity. To avoid the widespread objection that senescence is not found in nature and manifests itself only under laboratory conditions, Jones et al. [1] presented data on animals that live in the wild (mainly in nature reserves and game parks), except for domestic animals (sheep), laboratory animals (fruit flies and the nematode), and animals whose demographic structure cannot be recorded under natural conditions (rotifers, louse, and crab).
RESULTS AND DISCUSSION
The results are shown in three tables for different taxa (Table 1 for vascular plants and the brown alga; Table 2 for chordates (in this case vertebrates); Table 3 for the other animal phyla), which contain the English and Latin names of the species and specify to which taxa of higher rank they belong.
LS and mortality. Although the demographic trajectories shown in the figure vary over a broad range, careful analysis of the graphs has revealed that they can be divided into four large groups according to the degree of “accumulated mortality” (defined as the ratio of mortality at the terminal age and average mortality): strongly increasing with age (IV), markedly increasing (III), weakly increasing (II), and decreasing or constant (I).
Thus, for humans, which belong to group IV (Nos. 1-6 in figure and Table 2), this ratio was the highest: 23 for female Japanese (No. 1 in figure and Table 2), 13.5 (No. 2) for female Swedes and 7.5 for Ache Native Americans (No. 3). Such a pronounced growth of relative mortality with age that can be found in humans (and which emerged largely over the last century because of increasing LS95) was explained by the effects of behavioral and ecological changes (including advances of healthcare) rather than genetic changes [66-68].
This ratio is also high (8 and 7.5, respectively) in fish kept in captivity (No. 4, guppy) and birds (No. 3, the Bali mynah, which was on the verge of extinction, and its population size was supported by all possible means) [69].
The next group, group III, in which senescence is less pronounced, comprises more species (Nos. 7-18); it is more heterogeneous and includes the killer whale, lion, ungulates, and primates (baboon and chimpanzee), as well as the fruit fly, nematode worm, and rotifers. This group is characterized by considerable although less pronounced growth of mortality: from 5.5 in the killer whale (No. 7) to 3.5 in the chamois (No. 18).
Group II is characterized by rather low values of the ratio of mortality at the terminal age and average mortality: from 2.5 in the sheep (No. 19) to 1.2 in the agave (No. 30). Finally, group I, which comprises the greatest number of species (Nos. 31-48), is not characterized by any considerable changes in mortality with age (from 1.1 in the geonoma palm (No. 31) to 0.5 in the white mangrove (No. 48)); essentially, these species are non-senescent. Since the species were selected for analysis by Jones et al. [1] not for being preferably non-senescent but for providing the most comprehensive available data on survival, such a great number of species that successfully withstand aging is remarkable. It can be suggested that in many species LS95 is too different from the maximum LS, and 95% individuals in the population die before they can show any pronounced signs of senescence (as shown, e.g. in Table 2).
Fertility. Jones et al. [1] used fertility as the parameter of vitality. Using this parameter (in spite of its evolutionary importance), they could not reveal considerable variation in the studied series of organisms. Thus, considerable decrease in fertility with age can be observed only in the groups of species with strongly pronounced increase in mortality (groups III and IV; figure and Tables 2 and 3). In the other groups, independently of the taxon, fertility either remains constant or even increases. Even the decrease in fertility found at later ages (closer to LS95) is rather small, and there is almost no species in which the curve falls below the average level for the entire study period from the moment of maturity. If we disregard the most short-lived species (rotifers, nematode worm, and fruit flies), then a strong decrease in fertility is found only in some ungulates (red deer (No. 13) and chamois (No. 18)) and in two animals kept in captivity: guppy (No. 4) and Bali mynah (No. 3); only humans (Nos. 1, 3, 5) and killer whales (No. 7) (and partly chimpanzees, No. 16) additionally have bell-shaped fertility curves, with the peak reached already at a young age, i.e. these species have acquired a capability to live rather long during the post-reproductive period (figure). This suggests that such a phenomenon is widespread under the conditions of decreasing selection pressure [27, 28, 62, 63, 70]. It should be noted that all the above-mentioned species (humans, killer whales, and chimpanzees) are highly social and highly capable of learning. Therefore, their long post-reproductive periods could be an adaptation determined by the value of old, experienced individuals for the survival of groups and for raising the young (the so-called “grandmother hypothesis”; see e.g. [15]). For instance, it has been shown that old non-fertile killer whales more often become leaders of the school than fertile females or males, especially in years with deficient food resources [71].
Therefore, in spite of its evolutionary importance, fertility proved insufficient as a parameter for comparative analysis of the dynamics of senescence, although it confirmed the conclusions drawn from division of animals and plants into groups according to mortality curves (Tables 1-3).
In addition, the mortality and fertility trajectories of any species depend on the environment in which they are measured. Ecological and genotypic variations have been recorded in laboratory studies of nematodes, the Mediterranean fruit fly, Drosophila fruit fly, and other model species [5, 72]. In laboratory rats (Rattus norvegicus) and mice (Mus musculus), the shapes of mortality curves, although they clearly indicate that in these animals mortality considerably increases with age (see group III), show considerable variance of data (especially in mice), which probably reflects genetic changes that have accumulated under laboratory conditions [1].
Discussing non-senescent animals, we must separately mention the hydra and the naked mole rat (Heterocephalus glaber) [36, 73].
In the hydra (Hydra magnipapillata, No. 38) living in the laboratory, mortality risk, and stable for all adult ages, is so small that 5% of adults should remain alive after 1400 years [1]. Khokhlov suggested that destructive changes leading to biological senescence are triggered by cell proliferation limitation, which does not allow, “diluting” damaged cells in time with “fresh” undamaged cells [4, 74, 75]. This theory explains the existence of some non-senescent species, which display no degenerative changes over their entire life cycles, such as the hydra [75]. Nevertheless, data on other non-senescent species (tortoises, which grow much more slowly than the hydra and thus cannot have equally rapid renewal of cells) show that there are some non-senescent species with unlimited growth over their entire life (e.g. the giant tortoise Testudo gigantea or desert tortoise Gopherus agassizii), but there are also rather small tortoises that stop growing by an age of 30-40 years (e.g. the three-toed box turtle Terrapene carolina) [23, 76, 77].
Data on the mortality and fertility of the naked mole rat were provided by Buffenstein [36]. They were not used by Jones et al. because of the values of initial mortality, inadequate in their opinion. However, Jones et al. [1] used such a format of data representation in which mortality at the moment of sexual maturity rather than at birth was viewed as initial mortality. In this case the naked mole rat would belong to non-senescent animals (group I), occupying in the figure an honorable place next to the “immortal” hydra.
Views vary on the susceptibility of angiosperms to aging [78-80]. In our opinion, the available data reveal no clear signs of the Gompertz type of senescence in plants or algae (Table 1).
It was repeatedly stated [66, 81] that in plants, in contrast to animals, aged cells die rather than accumulate, and they do so in a programmed way rather than randomly. In addition, dead plant cells are not discarded, but included in supporting or vascular structures. Thus, plants may have evolved a mechanism that allows them to fight aging by means of programmed cell death.
Phylogenetic models of senescence. It has been suggested that asexual reproduction [82], modularity [83], absence of division into the germ line and soma [84, 85], absence of predator pressure and presence of protected shelters [86], capability of regeneration, and small number of cell types [87] in some cases can facilitate escape from senescence [1]. Many species of group I (reptiles, the coral, vascular plants, and the alga) continue growing to become much larger after reaching reproductive maturity. In these species with unlimited growth, mortality does not increase with age, whereas fertility somewhat increases; i.e. their aging patterns are principally different from those found in species with limited growth [25, 32, 60]. In addition, methods of computer modeling have shown that under some conditions sedentary, attached forms (known among both animals and plants) can evolve phenoptosis (programmed senescence and death) as a result of kin selection, and the evolutionary benefits of such acquisition have been proved [88].
As noted in the disposable soma theory [28], differences between species in LS and in the optimal distribution of resources between vital processes can help explain empirical data on differences in mortality and fertility trajectories [32, 89, 90]. Senescence rate decreases in evolutionary lineages with increasing body weight, duration of pregnancy, age of sexual maturity, and flight capacity [91].
It should also be noted that survival curves display the mortality of a general, genetically heterogeneous cohort. As the age of the cohort increases, the proportion of individuals that have genotypes conducive to longevity inevitably grows. If some individuals in the population acquire alleles that facilitate decelerated increase in the probability of death, the survival and mortality curve for the entire population will change [14, 25]. It is difficult to distinguish from survival curves a situation in which the probability of death of each individual decreases with age from a situation in which the probability of death of each individual remains constant, but initially the cohort was strongly polymorphic in alleles that affect longevity and therefore the proportion of individuals with inherited tendency to live long increases with time. This is partly confirmed by the opinion about decelerated mortality at later ages [15]. Gavrilov and Gavrilova [92] warned about the existing methodological difficulties, since according to their calculations the Gompertz law continues to work even in long-living individuals, until the age of 106 years in humans. In addition, those authors together with L. S. Yaguzhinsky showed as early as 1978 the existence of the so-called compensation effect: attempts to decrease the level of the age-related component of mortality in the Gompertz–Makeham equation (e.g. by improving environmental conditions) increase the relative rate of growth with age for this component [17, 19]. A number of genes have already been revealed that mutate to produce beneficial effects on LS through preventing age-related diseases (e.g. there are such data on the gene APOE) [15, 21]. An additional difficulty is the fact that LS in humans is rather poorly inherited and strongly depends on environmental conditions [21, 93]. One promising approach could be to study the so-called “blue zones” of the planet, in which the proportion of long-lived persons is dramatically higher than average; one of them is Okinawa, Japan [15]. In this case, the presence of a great number of centenarians would be conductive to growth of LS95 (figure and comments to it), and therefore, according to Jones, to prolongation of reliable survival curves to later ages and thus an opportunity to reveal genes responsible for longevity and decelerated growth of mortality.
It can be noted that for animals of groups III and IV (including humans; see figure and Table 2) (long-lived and senescent), the method of Jones et al. [1] characterizes mortality during almost the entire life cycle. The same is true of short-lived animals, e.g. the tundra vole or rotifers, whether they display the Gompertz type of senescence or not. As for long-lived species with a less pronounced increase (or even decrease) in mortality (e.g. the freshwater crocodile, desert tortoise, or Scots pine) and short-lived non-senescent animals, in them the Jones method can characterize only a small part of the life cycle and does not make it possible to judge how senescence manifests itself at later stages of the cycle. For instance, it is known that in old trees signs of senescence are rather clear [94, 95], but less than 5% of individuals that reach maturity survive to become senescent. As a result, senescence in trees cannot be analyzed by that method.
It seems clear from analysis of the graphs provided by Jones et al. [1] that many animals fall among the eliminated 95% long before they reach their maximum LS. This fact does not make the analysis less reliable if mortality already considerably increased before LS95 (e.g. as in groups III and IV) (Nos. 1-18 [1]) (figure and Tables 2 and 3). It should be notes that these groups include no plants or algae.
As for cases of intense mortality in nature caused mainly by environmental factors, it turns out that those authors fall into “the trap of Medawar”, who insisted that senescence does not exist in natural environments [62]. In fact, the size of the cohort in such cases, e.g. in the mute swan (No. 22), collared flycatcher (No. 35), or great tit (No. 37), falls very rapidly (figure); as a result, the cohort of animals that includes 5% surviving individuals long before they become old, is considered non-senescent. We tested this conclusion by comparison with data on the maximum LS of species from groups I and II (Table 2). Even though Jones et al. [1] repeatedly criticized maximum LS, this parameter is given in most databases and reference books on gerontology (e.g. [23, 33-35]).
For instance, Jones et al. [1] note that it was extremely difficult to find signs of either the Gompertz type of senescence or biological senescence in the mute swan [96]. LS95 of the swan (No. 22, group II; figure and Table 2) is 16 years, but it can live at least 29 years in nature and up to 70 years in captivity [97].
Role of phylogenetic relatedness. All mammals are concentrated in the upper part of figure (Table 2). It can be suggested that senescence is especially strong, apart from mammals, in species with the greatest number of postmitotic cells, i.e. insects (Table 3).
Considerable variation in senescence of the Gompertz type can be seen among birds, from the Bali mynah (No. 3, group IV) to the great tit (No. 37, group I) (Table 2). In spite of the conclusions of Jones et al. [1], large birds (fulmar, No. 6; swan, No. 22; sparrow hawk, No. 28) are also senescent, but their biological senescence can begin to manifest itself at a rather late age, which may be reached by less than 5% of the initial cohort. As for senescence of small birds, which are short-lived and have many enemies, it really cannot be revealed in nature, as predicted by Medawar [62].
Amphibians and reptiles fall into group I (only one species, the crocodile, No. 26, is in group II) and have flat mortality curves (figure and Table 2). Reptiles can live and remain capable of reproduction extremely long, but the proportion of long-lived individuals is probably also no greater than 5% of the initial cohort, and the dynamics of their senescence is also difficult to analyze by the Jones method (because it also requires that mortality until the terminal age LS95, which is nothing outstanding for these species, does not increase with age). Amphibians are represented in that study by only one species (the red-legged frog, No. 42), but most of the mortality curve was unfortunately obtained mathematically (figure). On the whole, frogs are not distinguished by great LS or resistance to senescence [23], in contrast to some caudate amphibians, such as the Japanese giant salamander (Megalobatrachus japonicus), olm (Proteus anguinus) (see above), or the spotted salamander (Ambystoma maculatum) [23, 37, 98].
Different invertebrate phyla are scattered among all groups, beginning with bdelloid rotifers and water fleas (group III; figure and Table 3), which have mortality curves similar to those of mammals.
Mollusks, represented in the study by the red abalone (No. 41), are known for their longevity and resistance to biological senescence [23, 99], but the champions in longevity and resistance to senescence among the animals considered are cnidarians – the hydra (No. 38) and the red gorgonian (No. 43). Furthermore, while the hydra is capable of displaying its exceptional abilities only in the laboratory [87], the red gorgonian, which grows in nature by 1-2 cm in height and 0.36 mm in diameter per year, can follow this pattern for several centuries and possibly even millennia [100, 101].
As noted above, we could not reveal from the provided data any signs of the Gompertz type of senescence in plants or algae (Table 1). In our opinion, data on changes in fertility have only confirmed the conclusion about lack of changes in their mortality with age. We suggested above that plants have evolved a mechanism of fighting aging by programmed cell death. Thus, we can rather tentatively state that the very definition of the term “senescence” as “increasing probability of death with age” requires some specification, because, as noted above, there is some discord between the Gompertz type of senescence and biological senescence. As for the often-used definition of biological aging as “processes that lead to increased probability of death with age”, it appears somewhat vague.
We have concluded that the classification proposed by Jones et al. [1] makes it possible to approximately divide animals and plants only by their levels of the Gompertz type of senescence, whereas susceptibility to biological senescence can be estimated only when principally different models are applied (see, e.g. [19, 21]).
We are grateful to V. V. Ashapkin and L. S. Yaguzhinsky for useful advice and comments provided in the course of our work on this study.
This study was supported by the Russian Science Foundation (project No. 14-50-00029).
REFERENCES
1.Jones, O. R., Scheuerlein, A., Salguero-Gomez, R.,
Camarda, C. G., Schaible, R., Casper, B. B., Dahlgren, J. P., Ehrlen,
J., Garcia, M. B., Menges, E. S., Quintana-Ascencio, P. F., Caswell,
H., Baudisch, A., and Vaupel, J. W. (2014) Diversity of ageing across
the tree of life, Nature, 505, 169-173.
2.Harman, D. (1956) Aging: a theory based on free
radical and radiation chemistry, J. Gerontol., 11,
298-300.
3.Emanuel’, N. M. (1982) Biology of
Ageing [in Russian], Nauka, Leningrad.
4.Khokhlov, A. N. (1988) Cell proliferation and
aging, in Advances in Science and Technology, General Problems of
Physico-Chemical Biology Series [in Russian], Vol. 9, VINITI,
Moscow.
5.Akif’ev, A. P., and Potapenko, A. I. (2001)
Nuclear genetic material as an initial substrate of aging in animals,
Russ. J. Genet., 37, 1213-1223.
6.Finkel, T., and Holbrook, N. J. (2000) Oxidants,
oxidative stress, and the biology of ageing, Nature, 408,
239-247.
7.Barja, G. (2004) Aging in vertebrates, and the
effect of caloric restriction: a mitochondrial free radical
production-DNA damage mechanism? Biol. Rev., 79,
235-251.
8.Stadtman, E. R. (1992) Protein oxidation and aging,
Science, 257, 1220-1224.
9.Hamilton, M. L., Van Remmen, H., Drake, J. A.,
Yang, H., Guo, Z. M., Kewitt, K., Walter, C. A., and Richardson, A.
(2001) Does oxidative damage to DNA increase with age? Proc. Natl.
Acad. Sci. USA, 98, 10469-10474.
10.Kujoth, G. C., Bradshaw, P. C., Haroon, S., and
Prolla, T. A. (2007) The role of mitochondrial DNA mutations in
mammalian aging, PLoS Genet., 3, 161-173.
11.Skulachev, M. V., and Skulachev, V. P. (2014) New
data on programmed aging – slow phenoptosis, Biochemistry
(Moscow), 79, 977-993.
12.Shilovsky, G. A., Khokhlov, A. N., and Shram, S.
I. (2013) The protein poly(ADP-ribosyl)ation system: its role in genome
stability and lifespan determination, Biochemistry (Moscow),
78, 433-444.
13.Pero, R. W., Holmgren, K., and Persson, L. (1985)
γ-Radiation induced ADP-ribosyl transferase activity and
mammalian longevity, Mutat. Res., 142, 69-73.
14.Finch, C. E. (1990) Longevity, Senescence and
the Genome, University Chicago Press, Chicago.
15.Austad, S. N. (1997) Why We Age, John
Wiley and Sons, New York.
16.Anisimov, V. N. (2008) Molecular and
Physiological Mechanism of Senescence [in Russian], Nauka, St.
Petersburg.
17.Gavrilov, L. A., Gavrilova, N. S., and
Yaguzhinsky, L. S. (1978) Basic patterns of aging and death in animals
from the standpoint of reliability theory, Zh. Obshch. Biol.,
39, 734-742.
18.Urlanis, B. Ts. (1978) Evolution of
Longevity [in Russian], Statistika, Moscow.
19.Gavrilov, L. A., and Gavrilova, N. S. (1991)
Biology of Longevity [in Russian], Nauka, Moscow.
20.Mamai, A. V. (2006) Mathematical model for
survival of organisms, Trudy ISA RAN, 19, 70-93.
21.Khalyavkin, A. V., and Yashin, A. I. (2007) in
Gerontology in silico: the Emergence of the New Discipline:
Mathematical Models, Analysis of Data, and Calculating Experiments
(Marchuk, G. I., Anisimov, V. N., Romaniukha, A. A., and Yashin, A. I.,
eds.) BINOM, Laboratoriya Znanii, Moscow.
22.Gompertz, B. (1825) On the nature of the function
expressive of the law of human mortality and on a new mode of
determining life contingencies, Philos. Trans. R. Soc. London,
115, 513-585.
23.Comfort, A. (1979) The Biology of
Senescence, Churchill Livingstone, Edinburgh-London.
24.McNamara, J. M., and Houston, A. I. (1996)
State-dependent life histories, Nature, 380, 215-221.
25.Finch, C. E. (1998) Variations in senescence and
longevity include the possibility of negligible senescence, J.
Gerontol. Biol. Sci., 53, 235-239.
26.Weismann, A. (1889) Essays upon Heredity and
Kindred Biological Problems, Clarendon Press, Oxford.
27.Williams, G. C. (1957) Pleiotropy, natural
selection and the evolution of senescence, Evolution, 11,
398-411.
28.Kirkwood, T. B. L. (1977) Evolution of ageing,
Nature, 270, 301-304.
29.Medvedev, Z. A. (1990) An attempt at a rational
classification of theories of ageing, Biol. Rev. Camb. Philos.
Soc., 65, 375-398.
30.Campisi, J. (2005) Aging, tumor suppression and
cancer: high wire-act! Mech. Ageing Dev., 126, 51-58.
31.Kirkwood, T. B. L. (2010) Systems biology of
ageing and longevity, Phil. Trans. R. Soc. B, 366,
64-70.
32.Baudisch, A. (2008) Inevitable Aging?
Contributions to Evolutionary-Demographic Theory,
Springer-Verlag, Berlin-Heidelberg.
33.Lamb, M. J. (1977) Biology of Aging, John
Wiley and Sons, New York.
34.Grzimek, B. (1990) Grzimek’s
Encyclopedia of Mammals, McGraw-Hill, New York.
35.Carey, J. R., and Judge, D. S. (2001)
Monographs on Population Aging, Ser. 8, Odense University Press,
Odense, Denmark.
36.Buffenstein, R. (2005) The naked mole-rat: a new
long-living model for human aging research, J. Gerontol.,
60, 1369-1377.
37.Voituron, Y., De Fraipont, M., Issartel, J.,
Guillaume, O., and Clobert, J. (2011) Extreme lifespan of the human
fish (Proteus anguinus): a challenge for ageing mechanisms,
Biol. Lett., 7, 105-107.
38.Skulachev, V. P. (1997) Aging is a specific
biological function rather than the result of a disorder in complex
living systems: biochemical evidence in support of Weismann’s
hypothesis, Biochemistry (Moscow), 62, 1191-1195.
39.Skulachev, V. P. (1999) Phenoptosis: programmed
death of an organism? Biochemistry (Moscow), 64,
1418-1426.
40.Skulachev, V. P. (2003) Aging and the programmed
death phenomena, in Top. Curr. Genet. Model Syst. Aging
(Nystrom, T., and Osiewacz, H. D., eds.) Springer-Verlag,
Berlin-Heidelberg.
41.Skulachev, V. P., and Longo, V. D. (2005) Aging
as a mitochondria-mediated atavistic program: can aging be switched
off? Ann. N. Y. Acad. Sci., 1057, 145-164.
42.Dawkins, R. (1999) The Extended Phenotype: the
Long Reach of the Gene, Oxford University Press, Oxford.
43.Longo, V. D., Mitteldorf, J., and Skulachev, V.
P. (2005) Programmed and altruistic ageing, Nat. Rev. Genet.,
6, 866-872.
44.Libertini, G. (2012) Classification of
phenoptotic phenomena, Biochemistry (Moscow), 77,
707-715.
45.Libertini, G. (2012) Phenoptosis, another
specialized neologism, or the mark of a widespread revolution?
Biochemistry (Moscow), 77, 795-798.
46.Skulachev, V. P. (2012) What is
“phenoptosis” and how to fight it? Biochemistry
(Moscow), 77, 689-706.
47.Terzibasi, E., Valenzano, D. R., and Cellerino,
A. (2007) The short-lived fish Nothobranchius furzeri as a new
model system for aging studies, Exp. Gerontol., 42,
81-89.
48.Weinert, B. T., and Timiras, P. S. (2003) Invited
review: theories of aging, J. Appl. Physiol., 95,
1706-1716.
49.Hoving, H. J., Perez, J. A., Bolstad, K. S.,
Braid, H. E., Evans, A. B., Fuchs, D., Judkins, H., Kelly, J. T.,
Marian, J. E., Nakajima, R., Piatkowski, U., Reid, A., Vecchione, M.,
and Xavier, J. C. (2014) The study of deep-sea cephalopods, Adv.
Mar. Biol., 67, 235-239.
50.Bradley, A. J., Mcdonald, I. R., and Lee, A. K.
(1980) Stress and mortality in a small marsupial (Antechinus
stuartii, Macleay), Gen. Comp. Endocrinol., 40,
188-200.
51.Lens, F., Smets, E., and Melzer, S. (2012) Stem
anatomy supports Arabidopsis thaliana as a model for insular
woodiness, New Phytol., 193, 12-17.
52.Melzer, S., Lens, F., Gennen, J., Vanneste, S.,
Rohde, A., and Beeckman, T. (2008) Flowering-time genes modulate
meristem determinacy and growth form in Arabidopsis thaliana,
Nat. Genet., 40, 1489-1492.
53.Lindoo, S. J., and Nooden, L. D. (1977) Studies
on behavior of senescence signal in Anoka soybeans, Plant
Physiol., 59, 1136-1140.
54.Nooden, L. D., and Murray, B. J. (1982)
Transmission of the monocarpic senescence signal via the xylem in
soybean, Plant Physiol., 69, 754-756.
55.Bowles, J. T. (1998) The evolution of aging: a
new approach to an old problem of biology, Med. Hypotheses,
51, 179-221.
56.Ashapkin, V. V., Kutueva, L. I., and Vanyushin,
B. F. (2015) Aging epigenetics: accumulation of errors or realization
of a specific program? Biochemistry (Moscow), 80,
1406-1417.
57.Boyd-Kirkup, J. D., Green, C. D., Wu, G., Wang,
D., and Han, J. D. (2013) Epigenomics and the regulation of aging,
Epigenomics, 5, 205-227.
58.Guarente, L., and Kenyon, C. (2000) Genetic
pathways that regulate ageing in model organisms, Nature,
408, 255-262.
59.Vijg, J., and Suh, Y. (2005) Genetics of
longevity and aging, Annu. Rev. Med., 56, 193-212.
60.Vaupel, J. W., Baudisch, A., Dolling, M., Roach,
D. A., and Gampe, J. (2004) The case for negative senescence, Theor.
Popul. Biol., 65, 339-351.
61.Chiang, C. L. (1984) The Life Table and Its
Applications, Robert E. Krieger Publishing Company, Malabar,
Florida.
62.Medawar, P. B. (1952) An Unsolved Problem of
Biology, H. C. Lewis and Co. Ltd, London.
63.Hamilton, W. D. (1966) The moulding of senescence
by natural selection, J. Theor. Biol., 12, 12-45.
64.Pearl, R., and Miner, J. R. (1935) Experimental
studies on the duration of life. XIV. The comparative mortality of
certain lower organisms, Q. Rev. Biol., 10, 60-79.
65.Deevey, E. S. (1947) Life tables for natural
populations of animals, Q. Rev. Biol., 22, 283-314.
66.Baudisch, A. (2011) The pace and shape of ageing,
Methods Ecol. Evol., 2, 375-382.
67.Oeppen, J., and Vaupel, J. W. (2002) Broken
limits to life expectancy, Science, 296, 1029-1031.
68.Burger, O., Baudisch, A., and Vaupel, J. W.
(2012) Human mortality improvement in evolutionary context, Proc.
Natl. Acad. Sci. USA, 109, 18210-18214.
69.Ricklefs, R. E., Scheuerlein, A., and Cohen, A.
(2003) Age-related patterns of fertility in captive populations of
birds and mammals, Exp. Gerontol., 38, 741-745.
70.Cohen, A. A. (2004) Female post-reproductive
lifespan: a general mammalian trait, Biol. Rev. Camb. Philos.
Soc., 79, 733-750.
71.Brent, L. J., Franks, D. W., Foster, E. A.,
Balcomb, K. C., Cant, M. A., and Croft, D. P. (2015) Ecological
knowledge, leadership, and the evolution of menopause in killer whales,
Curr. Biol., 25, 746-750.
72.Vaupel, J. W., Carey, J. R., Christensen, K.,
Johnson, T. E., Yashin, A. I., Holm, N. V., Iachine, I. A., Kannisto,
V., Khazaeli, A. A., Liedo, P., Longo, V. D., Zeng, Y., Manton, K. G.,
and Curtsinger, J. W. (1998) Biodemographic trajectories of longevity,
Science, 280, 855-860.
73.Skulachev, M. V., Severin, F. F., and Skulachev,
V. P. (2015) Aging as an evolvability-increasing program, which can be
switched off by organism to mobilize additional resources for survival,
Curr. Aging Sci., 8, 95-109.
74.Khokhlov, A. N. (2010) Does aging need an own
program or the existing development program is more than enough,
Russ. J. Gen. Chem., 80, 1507-1513.
75.Khokhlov, A. N. (2014) On the immortal hydra.
Again, Mosc. Univ. Biol. Sci. Bull., 69, 153-157.
76.Sergeev, A. M. (1937) Materials contributing to
the problem of postembryonic growth in reptiles, Zool. Zh.,
16, 723.
77.Miller, J. K. (2001) Escaping senescence:
demographic data from the three-toed box turtle (Terrapene carolina
triunguis), Exp. Gerontol., 36, 829-832.
78.Salguero-Gomez, R., Shefferson, R. P., and
Hutchings, M. J. (2013) Plants do not count… or do they? New
perspectives on the universality of senescence, J. Ecol.,
101, 545-554.
79.Shefferson, R. P., and Roach, D. A. (2013)
Longitudinal analysis in Plantago: strength of selection and reverse
age analysis reveal age-indeterminate senescence, J. Ecol.,
101, 577-584.
80.Tuomi, J., Crone, E., Gremer, J., Jakalaniemi,
A., Lesica, P., Pedersen, B., and Ramula, S. (2013) Prolonged dormancy
interacts with senescence for two perennial herbs, J. Ecol.,
101, 566-576.
81.Hayflick, L., and Butler, R. N. (1994) How and
Why We Age, Ballantine Books, New York.
82.Bell, G. (1984) Measuring the cost of
reproduction. I. The correlation structure of the life table of a plank
rotifer, Evolution, 38, 300-313.
83.Franco, M., and Silvertown, J. (1996) Life
history variation in plants: an exploration of the fast-slow continuum
hypothesis, Phil. Trans. R. Soc. B, 351, 1341-1348.
84.Buss, L. W. (1988) Diversification and germ-line
determination, Paleobiology, 14, 313-321.
85.Martinez, D. E., and Levinton, J. S. (1992)
Asexual metazoans undergo senescence, Proc. Natl. Acad. Sci.
USA, 89, 9920-9923.
86.Baudisch, A., and Vaupel, J. (2010) Senescence
vs. sustenance: evolutionary-demographic models of aging, Demogr.
Res., 23, 655-668.
87.Martinez, D. E. (1998) Mortality patterns suggest
lack of senescence in hydra, Exp. Gerontol., 33,
217-225.
88.Markov, A. V. (2012) Can kin selection facilitate
the evolution of the genetic program of senescence? Biochemistry
(Moscow), 77, 733-741.
89.Caswell, H. (2012) Matrix models and sensitivity
analysis of populations classified by age and stage: a vec-permutation
matrix approach, Theor. Ecol., 5, 403-417.
90.Gadgil, M., and Bossert, W. H. (1970) Life
historical consequences of natural selection, Am. Nat.,
104, 1-24.
91.Ricklefs, R. E. (2010) Life-history connections
to rates of aging in terrestrial vertebrates, Proc. Natl. Acad. Sci.
USA, 107, 10314-10319.
92.Gavrilov, L. A., and Gavrilova, N. S. (2002)
Evolutionary theories of aging and longevity, Sci. World J.,
2, 339-356.
93.Khalyavkin, A. V. (2001) Influence of environment
on the mortality pattern of potentially non-senescent organisms.
General approach and comparison with real populations, Adv.
Gerontol., 7, 46-49.
94.Dubrovitskaya, N. I. (1961) Regeneration and
Age-Related Variations in Plants [in Russian], AN SSSR, Moscow.
95.Markov, M. V. (1986) Population Biology of
Plants [in Russian], Kazan University Press, Kazan.
96.Charmantier, A., Perrins, C., McCleery, R. H.,
and Sheldon, B. C. (2006) Quantitative genetics of age at reproduction
in wild swans: support for antagonistic pleiotropy models of
senescence, Proc. Natl. Acad. Sci. USA, 103,
6587-6592.
97.Terres, J. (1980) The Audubon Society
Encyclopedia of North American Birds, Knopf, New York.
98.Gillooly, J. F., Brown, J. H., West, G. B.,
Savage, V. M., and Charnov, E. L. (2001) Effects of size and
temperature on metabolic rate, Science, 293,
2248-2251.
99.Ungvari, Z., Sosnowska, D., Mason, J. B., Gruber,
H., Lee, S. W., Schwartz, T. S., Brown, M. K, Storm, N. J., Fortney,
K., Sowa, J., Byrne, A. B., Kurz, T., Levy, E., Sonntag, W. E., Austad,
S. N., Csiszar, A., and Ridgway, I. (2013) Resistance to genotoxic
stresses in Arctica islandica, the longest living noncolonial animal:
is extreme longevity associated with a multistress resistance
phenotype? J. Gerontol. A Biol. Sci. Med. Sci., 68,
521-529.
100.Druffel, E. R., Griffin, M. S., Witter, A.,
Nelson, E., Southon, J., Kashgarian, M., and Vogel, J. (1995) Gerardia:
bristlecone pine of the deep-sea? Geochim. Cosmochim. Acta,
59, 5031-5036.
101.Andrews, A. H., Cordes, E. E., Mahoney, M. M.,
Munk, K., Coale, K. H., Cailliet, G. M., and Heifetz, J. (2002) Age,
growth, and radiometric age validation of a deep-sea, habitat-forming
gorgonian (Primnoa resedaeformis) from the Gulf of Alaska,
Hydrobiologia, 471, 101-110.