Temperature Dependence of Tryptophan Fluorescence Lifetime in Aqueous Glycerol and Trehalose Solutions
V. V. Gorokhov, P. P. Knox, B. N. Korvatovskiy, N. Kh. Seifullina, S. N. Goryachev, and V. Z. Paschenko*
Lomonosov Moscow State University, Faculty of Biology, 119991 Moscow, Russia; E-mail: vz.paschenko@gmail.com* To whom correspondence should be addressed.
Received June 15, 2017; Revision received August 15, 2017
The temperature dependences of tryptophan fluorescence decay kinetics in aqueous glycerol and 1 M trehalose solutions were examined. The fluorescence decay kinetics were recorded in the spectral region of 292.5-417.5 nm with nanosecond time resolution. The kinetics curves were approximated by the sum of three exponential terms, and the spectral distribution (DAS) of these components was determined. An antisymbatic course of fluorescence decay times of two (fast and medium) components in the temperature range from –60 to +10°C was observed. The third (slow) component showed only slight temperature dependence. The antisymbatic behavior of fluorescence lifetimes of the fast and medium components was explained on the assumption that some of the excited tryptophan molecules are transferred from a short-wavelength B-form with short fluorescence lifetime to a long-wavelength R-form with an intermediate fluorescence lifetime. This transfer occurred in the indicated temperature range.
KEY WORDS: tryptophans, rotamers, fluorescence, temperature dependence, fluorescence decay kineticsDOI: 10.1134/S0006297917110049
Abbreviations: DAS, decay-associated spectra.
Functional activity of proteins depends to a large extent on their
conformational dynamics – their ability to undergo
conformational rearrangements required for their specific functions [1]. It is generally recognized that fast stochastic
structural fluctuations on the pico- or nanosecond time scale [2] between various substates of protein molecules play
a crucial role in functionally significant conformational changes [3]. It has been suggested that proteins are
characterized by an extensive set of these conformational substates
separated by local energy barriers reflecting the complexity of their
energy profiles. Because the heights of these energy barriers can vary
significantly, the time scale of protein mobility can cover several of
orders of magnitude [4, 5].
Stochastic protein mobility decreases with decrease in temperature and,
thus, can be localized in a time scale characteristic for specific
functional process mediated by the protein. The type and number of
surrounding solvent molecules (primarily water) also affect dynamic
characteristic of a protein. These molecules create a local surface
layer that can act as a plasticizer or, vice versa, as a stabilizer of
conformational modes, thus enhancing or hindering transitions between
these conformational substates, respectively [3, 6]. Hence, protein dynamics that defines its
functional activity can be modified not only by the temperature factor,
but also via introduction of the protein into a polymer gel matrix,
dehydration, as well as solvation with various cryosolvents [6-9]. Malferrari et al. [10] investigated the effect of hydration and
dehydration of a trehalose matrix on the reduction kinetics of the
primary donor of PS1, P700•+. The re-dehydration of the
trehalose matrix at room temperature imitated the effect of freezing of
PS1 in the aqueous glycerol solution. Simultaneous investigation of
dynamic and functional indicators of enzymes under varying conditions
of temperature and solvent composition is a powerful tool for
investigation of the mechanisms of the processes mediated by these
proteins.
Fluorescence spectroscopy of tryptophan residues in proteins is widely used as an intrinsic indicator of protein conformation, its dynamics, and intermolecular interactions. It is known that the dynamic (spectral-kinetic) behavior of tryptophan molecules is very sensitive to the state of their environment [11, 12]. Fluorescence of the indole chromophore is highly sensitive to the state of its environment and, as a result, it serves as an indicator of even minor changes in this environment [13]. If a protein structure is known, then it is possible in principle to interpret the changes in tryptophan fluorescence in terms of structural changes at the level of atomic resolution. The location of the maximum of the protein tryptophanyl fluorescence spectrum that is defined by the relaxation characteristics of the polar environment of the excited chromophore has long been used as an indicator of protein intramolecular dynamics during, for example, temperature increase or decrease [14, 15]. It is more difficult, however, to interpret the effect of environment on the lifetime of protein tryptophanyl fluorescence. Detailed elucidation of the nature of local changes near tryptophan residues that affect experimentally obtained temperature dependences of fluorescence lifetimes requires detailed and complex investigation. One possible approach to this problem is investigation of the temperature dependences of tryptophan fluorescence lifetimes in different media, which is the subject of this work.
MATERIALS AND METHODS
Fluorescence kinetics were recorded with a PML-16 setup with time- and wavelength-correlated single photon counting (Becker & Hickl, Germany). This instrument is equipped with a Hamamatsu R5900 16-channel multianode PMT containing 16 separate output anode elements and a common cathode and dynode system. The fluorescence signal passes through a polychromator equipped with a diffraction grating (600 lines/mm) providing a 200-nm spectral band of the measuring system with resolution of 12.5 nm/channel. This allows recording of three-dimensional fluorescence patterns reflecting changes in lifetime (τ), spectrum (λ), and intensity (I) of the emission. Fluorescence of the sample was excited at 280 nm using an EPLED 280 picosecond pulsed semiconductor diode (Edinburg Photonics, Scotland), pulse duration 870 ps, spectral width 10 nm, pulse frequency 10 MHz, signal accumulation time 30 s. Thus, by recording the 3D (t, λ, I) image of tryptophanyl emission, we measured kinetics of fluorescence decay for each spectral channel in the range 292.5-417.5 nm. During the measurement, the sample was in a cuvette cooled with liquid nitrogen with temperature controlled using a thermocouple. Time of cooling to –180°C was ~10 min, rate of subsequent heating was 5-7°C/min. Tryptophan and trehalose from Sigma (USA) and glycerol from Merck (Germany) were used in the study. Tryptophan concentration in the sample was 10 mM.
The massive spectral-kinetic dataset obtained from the measurements comprises a set of fluorescence decay kinetics recorded in different spectral channels in the range of wavelengths 292.5-417.5 nm with 12.5-nm interval. The number of experimental points in each kinetic curve is 4096. The number of photons detected in this region of the spectrum was also recorded for each channel.
The experimental kinetics were approximated for each spectral channel using the SPCImage program (Becker & Hickl) based on Eq. (1):
where ai(λ) is a wavelength-dependent preexponential factor of the component with lifetime τi, and i designates the number of the component.
This program deconvolutes the kinetics using the Marquardt–Levenberg algorithm into the sum of one to five exponents convoluted with the hardware IRF function measured for each spectral channel. We limited ourselves to three exponents because further increase of the number of exponents did not result in decrease in χr2. In the first step, parameters ai and τi were varied for each spectral channel. Next, the τi values (1 ≤ i ≤ 3) were averaged over all spectral channels. The averaged τi data were inserted into the Globals Unlimited program for global analysis over all spectral channels (University of Illinois) as nonvariable parameters for the final determination of preexponential coefficients ai(λ), which then were used for construction of DAS (decay-associated spectra) for each component. The standard error of approximation χr2 was calculated using Eq. (2):
where dj are experimental values of the fluorescence decay kinetics at time point j, fj the value of the calculated theoretical curve for this time point, which was equal to function (1) convoluted with the hardware function (f = FIRF), N is number of experimental points, and p the number of parameters of the theoretical curve.
The χr2 values were averaged over all spectral channels. In our calculation, the calculated average value of χr2 did not exceed 1.4 in the case of the three-exponential approximation, while the values of χr2 were above 1.8 in the case of the biexponential approximation. Hence the three-exponential approximation was used in all calculations.
RESULTS AND DISCUSSION
In this work, we thoroughly investigated temperature dependences of tryptophan fluorescence lifetimes in 50% aqueous glycerol solution and in 1 M aqueous trehalose solution. The fluorescence decay kinetics at room temperature in both cases can be approximated reasonably well by three exponentials with lifetimes τ1 ≈ 4 ± 0.05 ns, τ2 ≈ 6.5 ± 0.08 ns, and τ3 ≈ 12.5 ± 0.2 ns. According to our previous study [16], the complex character of tryptophan fluorescence decay in solution and in the protein composition can be explained by the availability of three possible rotamers of indole rings about the Cα–Cβ bond that emerge from electrostatic interactions in the tryptophan molecule. Moreover, the population of one of the rotamers is usually significantly higher than of the other two. In turn, one of the rotamers is predominant between the remaining two rotamers.
In the case of tryptophans located in a protein matrix, micro-conformational states of the protein near the indole ring are the specific causes of heterogeneity of the kinetics of the recorded signal in addition to the apparent rotamers of the tryptophan side chain. Hence, it is more accurate to identify conformers in proteins rather than rotamers [17]. To describe the tryptophan fluorescence decay kinetics in a protein, a continuous distribution of lifetimes is more suitable than a description using a set of discrete exponentials. The basis for such distribution from the point of view of physics is represented by inter-transitions between various conformations, each characterized with a quasi-continuum of energy substates of the tryptophan residue in a different environment [17].
At the same time, the description with discrete exponentials can provide an adequate qualitative picture of the changes in the state of fluorescent chromophores occurring in the investigated samples with temperature varying over a wide range. We modeled this situation for the recorded temperature dependence of the fluorescence kinetics of tryptophan solutions in glycerol and trehalose.
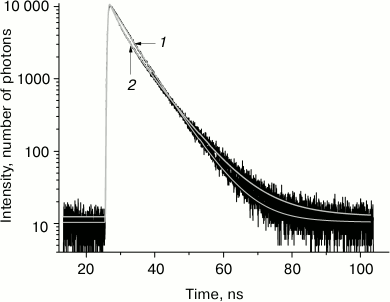
The kinetics of tryptophan fluorescence decay and its three-exponential approximation at temperatures –100 and –30°C are presented in Fig. 1. The three-exponential approximation describes well the kinetics of tryptophan fluorescence decay. The accuracy of determination of the shortest fluorescence lifetime in this three-exponential approximation is ±50 ps, intermediate lifetime ±80 ps, and the longer lifetime ±200 ps (with 95% confidence level).
Fig. 1. Tryptophan fluorescence decay kinetics in glycerol at temperature –100°C (1) and –30°C (2) at wavelength 330 nm.
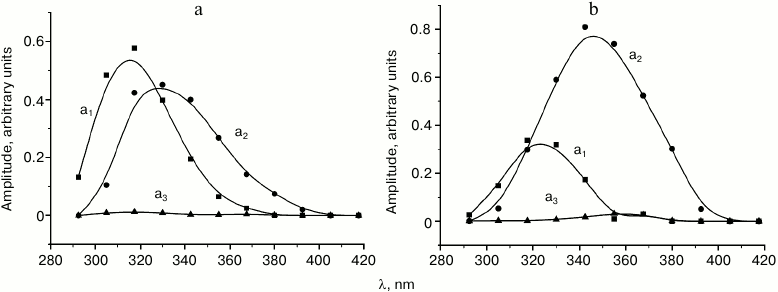
The examples of the resulting set of Decay Associated Spectra for the three-exponential approximation of the tryptophan fluorescence decay kinetics in solution at –100 and –30°C are presented in Fig. 2.
Fig. 2. Decay associated spectra (DAS) for the three-exponential approximation of tryptophan fluorescence decay kinetics at –100°C (a) and –30°C (b). The spectra of the fast, intermediate, and slow components are indicated with squares, circles, and triangles, respectively.
The results of analysis of spectral-temporal parameters of the fluorescence kinetics (Fig. 1) demonstrated that at low temperatures tryptophan in the investigated samples was present predominately as two rotamer forms corresponding to the short wavelength (“blue”, B) and long wavelength (“red”, R) region of the fluorescence spectrum. The B-form is characterized by a lifetime of τ1 ≈ 4.8 ns at the temperature of liquid nitrogen and fluorescence maximum at 295 nm; the lifetime of the R-form at this temperature is τ2 ≈ 6.5 ns and the fluorescence maximum is at approximately 315 nm. The contribution of the third form with τ3 = 12.5 ns was so negligible that it was not considered in the following kinetic analysis.
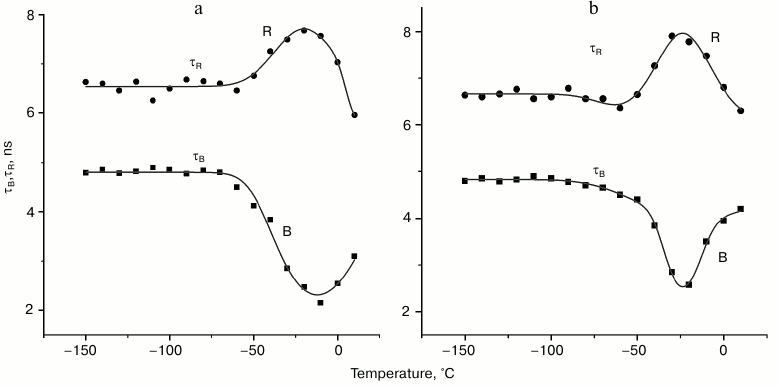
The temperature dependences of the fluorescence lifetimes of the B- and R-forms of the tryptophan rotamers in aqueous glycerol (panel (a)) and trehalose (panel (b)) solutions are presented in Fig. 3. One can see that τB and τR change only slightly in the temperature range from –180 to –60°C. Further increase in the temperature results in the decrease in τB from 4.8 to 2.2 ns with a minimum reached –13°C; τB starts to increase again with the following increase in temperature. On the other hand, τR increases in the temperature range from –60 to –15°C followed by its decrease. The relative contributions of the B- and R-forms to the total fluorescence signal at –100°C is 0.47 and 0.53, while at –30°C these contributions are 0.1 and 0.9, respectively. The level of contributions from different rotamer forms to the total fluorescence signal F was determined using Eq. (3):
where SB(R) are areas of spectral amplitudes of kinetic components with lifetimes τB and τR (a1 and a2 in Fig. 2, the contribution of the third component was not considered). Obviously, there is a transfer of emission energy from the B-form to the R-form.
Fig. 3. Temperature dependences of fluorescence lifetimes of B- and R-forms of tryptophan in aqueous glycerol (a) and trehalose (b) solutions. Temperature dependence was approximated with Eqs. (4).
It follows from our data that the lifetimes of kinetic components (Fig. 3) and their spectral amplitudes (data not shown) depend on the temperature. The fact of existence of a temperature region where the fluorescence lifetimes of B- and R-forms of tryptophan change in antisymbatic manner is characteristic for both aqueous glycerol and trehalose solutions. The lifetime for the third component remained practically unchanged (data not shown); moreover, its spectral amplitude was insignificant (Fig. 2). The region of transfer of the part of B-rotamers to the R-form is the temperature region above –50°C (see Fig. 3). This is the region were thawing of the used glass-like solutions occurs. For example, it follows from differential scanning calorimetry data that the glass transition temperature (Tg) of the ~30% trehalose solution (w/w) is approximately –42°C [18]. According to the data of Olsson et al. [18], trehalose solution at this concentration partially crystalizes during heating from the glass transition temperature (Tg) to the melting point (approximately –10°C). In other words, significant changes in intramolecular dynamic of the system occur during the heating of the glass-like solution in this temperature range, which cause the observed transition between the tryptophan rotamers. Similar processes obviously occur during heating of frozen 50% glycerol solution.
Hence, the conditions for transition of the part of B-rotamers into R-rotamers develop at a certain temperature of the medium. As will be shown below, this occurs when the intersection point of energy surfaces of electronic excited states of the two rotamers is in the overlapping of the spectra of local vibration of these rotamers in this energy region. As a result, the rate of the fluorescence decay of B-rotamers increases (decrease in lifetime) and the rate of fluorescence decay of R-rotamers decreases (increase in lifetime). The conditions for the B*→R* transition must be of resonance nature such as Gaussian dependence similar to overlapping of local vibrational spectra.
The temperature dependences of the fluorescence decay rate constants for the B- and R-forms of tryptophan were approximated by Eqs. (4), where the terms with Gaussian function describe resonance transfer from one rotamer form to the other:
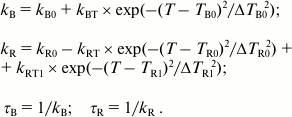 (4)
(4)The temperature in Eqs. (4) is expressed in the Celsius scale, kB and kR indicate rate constants of fluorescence decay of the B- and R-forms of tryptophan, kB0 and kR0 are the rate constants of fluorescence decay of the B- and R-forms in the absence of B*→R* transfer, parameter kBT is the amplitude of the rate of transfer from B*- to R*-form, and kRT defines the maximum increase in the fluorescence lifetime of the R-form. Parameters TB0 and ΔTB0 designate the center and width of the temperature interval favorable for the transfer of B-from to R-form, and parameters kR0, TR0, and ΔTR0 describe the change in the rate constant of the fluorescence decay of the R-form resulting from the B*→R* transfer. To have a more accurate approximation of the temperature dependence of kR, it was necessary to assume that a channel for transfer of the R*-form to the third rotamer form emerges at higher temperature (T > –10°C). Parameters kRT1, TR1, and ΔTR1 describe the resonance transfer of R*-form of tryptophan to the third rotamer form resulting in a decrease in the fluorescence lifetime of the R-form. The parameters τB and τR represent fluorescence lifetime of forms B and R, respectively. Both forward (B*→R*) and reverse (R*→B*) transfers are considered in this model.
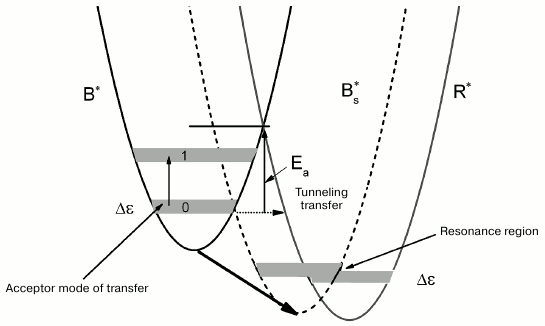
The types of tryptophan rotamers (1), (2), and (3) corresponding to the fluorescence lifetimes τ1, τ2, and τ3 are defined by the rotation of the indole ring about the Cα–Cβ bond by different angles (0° (1), 60° (2), and 120° (3)). The transfer from rotamer (1)* to rotamer (2)* (asterisk indicates excited states of rotamers) is accompanied by overcoming the potential barrier of ~4.4 kcal/mol (Ea ≈ 1550 cm–1) [19]. The suggested scheme for the dynamics of potential energy surfaces for the accepting modes of tryptophan rotamers in the excited state is shown in Fig. 4. This scheme is based on the following. The over-barrier transition from the B*-form to the R*-form is hindered in this arrangement of potential energy surfaces due to the large value of Ea. However, if one assumes that the relative position of the tryptophan indole rings changes with an increase in temperature, the potential energy surface of the B*-form comes closer to the potential energy surface of the R*-form, and under these conditions the B*→R* transfer is significantly easier.
A local mode approximation is valid for description of nonradiative transfer in aromatic benzene-type molecules when various oscillations of valent bonds are considered as acceptor modes [20]. The transfer acceptor modes for aromatic cyclic compounds are associated with vibration of C–H-groups, and the distances between the vibrational levels are large in this case (Fig. 4). We assume that the deformational vibrations out of the plane of the indole macrocycle with frequency of ~1300 cm–1 are active for the B*→R* transfer [21]. The accepting mode of the B*→R* transfer at low and room temperatures is most probably in the ground state (Fig. 4); moreover, the distance between the zero and the first vibrational level for deformational vibrations is ~1300 cm–1. In the case of moderately high energy of the medium, reorganization of the activation barrier for the transfer is high (Fig. 4, Ea). As a result, as we mentioned before, under normal conditions the transfer of the B*-rotamer to the R*-rotamer proceeds via a tunneling mechanism with a low rate. In the case when temperature changes in the region of the medium glass transition, significant fluctuation of the environment near tryptophan can occur, including micro-conformational transfers related to rearrangement of hydrogen bonds and charged groups. Such process can cause rotation of the indole cycle in the B*-rotamer by a certain angle in the direction of its position in the R*-rotamer, which causes a shift of the potential energy surface of the B*-state towards the potential energy of the R*-state, and, as a result, reduction of the energy of reorganization and decrease in the B*→R* transfer activation barrier (Fig. 4). Furthermore, the vibrational spectra of the acceptor mode for different potential energy surfaces can align at certain temperature, and, as a result, the deformational vibration mode becomes active for the B*→R* transfer. This situation is depicted in Fig. 4 as an intermediate position of the potential energy surface of Bs*.
Fig. 4. Schematic representation of the dynamics of potential energy surfaces of excited states of tryptophan rotamer forms B* and R* with increasing temperature. Shift of the potential energy surface of B* towards potential energy surface of R* with change in temperature is indicated with bold arrow; Ea is activation energy of B*→R* transfer; Bs* is intermediate state of the potential energy surface; zero and first levels of vibrational energy of B-rotamer depicted by 0 and 1, respectively; Δε is width of the spectrum of the acceptor mode.
Hence, overlapping (resonance) of the local vibrational spectra of the excited tryptophan rotamer forms B* and R* can occur with change in temperature. Resonance, i.e. maximum overlapping of the vibrational spectra of the accepting mode of different rotamer forms in the region of interception of the terms of the excited states of two tryptophan terms, takes place at a certain temperature that corresponds to the maximum rate of the B*→R* transfer (Fig. 4). Further increase in temperature disrupts this resonance. The decay time τB begins returning to its initial value of 4.8 ns. However, the decay time τR does not return to its initial value of 6.5 ns, but continues to decrease even at T > 0°C, it drops below 6 ns, because the additional channel of fluorescence quenching likely opens for the R-form such as a transfer channel of this rotamer to the third form.
It must be mentioned that the correct description of the antisymbatic nature of the temperature dependences of the tryptophan fluorescence lifetimes is possible only on the assumption that the B→R transfer occurs in the excited state of tryptophan. Indeed, the intramolecular rate constant of the fluorescence decay does not depend on temperature. The temperature dependence of the lifetime of the excited state of molecules emerges due to their intercombinational conversion into a triplet state or nonradiative transfer to the ground state [22, 23]. The temperature dependence of the fluorescence lifetimes displays Arrhenius character in this case. In our case, in addition to the mechanisms cited above, the antisymbatic character of the temperature dependence of the fluorescence lifetimes of the B- and R-forms occurs because of the transition of the tryptophan B-form into the R-form in the singlet excited state – B*→R* transfer. We suggest that the decrease in the τB value with the increase in temperature from –60 to –10°C occurs because of the opening of an additional channel of deactivation of the B*-form – its transition to the R*-form. Further increase in the temperature disrupts the resonance between the spectra of local vibrations, and, as a result, τB begins returning to the initial level.
The results of approximation show that the location of the center of Gaussian components of the temperature dependence of the fluorescence decay, its width in the temperature region of the B*→R* transfer, as well as the amplitude are different in aqueous glycerol and trehalose solutions. The center of the Gaussian curve of the temperature region is around –13°C for tryptophan in aqueous glycerol solution and –23°C in trehalose. The width at half-maximum of the Gaussian component of the temperature curve is 40°C (28 cm–1) for tryptophan in aqueous glycerol solution and 30°C (21 cm–1) for tryptophan in trehalose. The maximum rate of the B*→R* transfer in aqueous glycerol solution is 2.2·108 s–1. This rate is slightly lower for the trehalose solution – 1.8·108 s–1.
The fact that the distribution of local vibrational energies favorable for the B*→R* transfer in trehalose is narrow in comparison with tryptophan in aqueous glycerol solution attracted our attention. This is likely related to the crystalline-like structure of trehalose, which causes the effect of depletion of the spectrum of local vibrations near the tryptophan molecule somewhat like the Shpolskii effect in crystalline matrices at low temperatures.
We established that tryptophans exist in at least three rotamer forms in aqueous glycerol and trehalose solutions that differ both in emission spectra and fluorescence lifetimes. For the first time, an unusual non-monotonous dependence of the fluorescence lifetimes of rotamers on temperature was observed; moreover, in the temperature range from –60 to +10°C, there was an antisymbatic change of τB relative to τR. We observed a very similar dependence of the tryptophan fluorescence in photosynthetic reaction centers of purple bacteria (unpublished data). A model was suggested to explain the antisymbatic pattern of the temperature dependence of τB and τR of tryptophans in solution according to which conditions develop in a certain temperature range for the transfer of the excited forms of one rotamer form (B*) to the other (R*). This becomes possible if the intersection points of electronic energy surfaces of the excited states of these two rotamers are near local vibrational spectra overlap, thus creating resonance. Outside this temperature region, the resonance between vibrational levels is disrupted, and, as a result, the fluorescence lifetimes do not depend on temperature. There is the possibility of another explanation for the observed effects. We continue investigation on this topic and hope to determine the nature of antisymbatic temperature dependence of τB and τR more accurately.
Acknowledgments
This work was financially supported by the Russian Foundation for Basic Research (project No. 15-29-01167).
REFERENCES
1.Frauenfelder, H., and McMahon, B. (1998) Dynamics
and function of proteins: the search for general concepts, Proc.
Natl. Acad. Sci. USA, 95, 4795-4797.
2.Fitter, J., Lechner, R. E., Buldt, G., and Dencher,
N. A. (1996) Internal molecular motions of bacteriorhodopsin:
hydration-induced flexibility studied by quasielastic incoherent
neutron scattering using oriented purple membranes, Proc. Natl.
Acad. Sci. USA, 93, 7600-7605.
3.Frauenfelder, H., Sligar, S. G., and Wolynes, P. G.
(1991) The energy landscapes and motions of proteins, Science,
254, 1598-1603.
4.Jackson, T. A., Lim, M., and Anfinrud, P. A. (1994)
Complex nonexponential relaxation in myoglobin after photodissociation
of MbCO: measurement and analysis from 2 ps to 56 µs,
Chem. Phys., 180, 131-140.
5.Johnson, J. B., Lamb, D. C., Frauenfelder, H.,
Muller, J. D., McMahon, B., Nienhaus, G. U., and Young, R. D. (1996)
Ligand binding to heme proteins, Biophys. J., 71,
1563-1573.
6.Paciarony, A., Cinelli, S., and Onori, G. (2002)
Effect of the environment on the protein dynamical transition: a
neutron scattering study, Biophys. J., 83, 1157-1164.
7.Palazzo, G., Mallardi, A., Hochkoeppler, A.,
Cordone, L., and Venturoli, G. (2002) Electron transfer kinetics in
photosynthetic reaction centers embedded in trehalose glasses: trapping
of conformational substates at room temperature, Biophys. J.,
82, 558-568.
8.Kriegl, J. M., Forster, F. K., and Nienhaus, G. U.
(2003) Charge recombination and protein dynamics in bacterial
photosynthetic reaction centers entrapped in a sol-gel matrix,
Biophys. J., 85, 1851-1870.
9.Mei, G., Di Venere, A., Agro, A. F., De Matteis,
F., and Rosato, N. (2003) Dipolar relaxation times of tryptophan and
tyrosine in glycerol and in proteins: a direct evaluation from their
fluorescence decays, J. Fluoresc., 13, 467-477.
10.Malferrari, M., Savitsky, A., Mamedov, M. D.,
Milanovsky, G. E., Lubitz, W., Mobius, K., Semenov, A. Yu., and
Venturoli, G. (2016) Trehalose matrix effects on charge-recombination
kinetics in photosystem I of oxygenic photosynthesis at different
dehydration levels, Biochim. Biophys. Acta, 1857,
1440-1454.
11.Schlamadinger, D. E., Gable, J. E., and Kim, J.
E. (2009) Hydrogen bonding and solvent polarity markers in the UV
resonance Raman spectrum of tryptophan: application to membrane
proteins, J. Phys. Chem. B, 113, 14769-14778.
12.Dashnau, J. L., Zelent, B., and Vanderkooi, J. M.
(2005) Tryptophan interactions with glycerol/water and
trehalose/sucrose cryosolvents: infrared and fluorescence spectroscopy
and ab initio calculations, Biophys. Chem., 114,
71-83.
13.Chen, Y., and Barkley, M. D. (1998) Toward
understanding tryptophan fluorescence in proteins, Biochemistry,
3, 9976-9982.
14.Burshtein, E. A. (1983) Intrinsic protein
luminescence as a tool for studying fast structural dynamics, Mol.
Biol. (Moscow), 17, 455-467.
15.Knox, P. P., Korvatovsky, B. N., Krasilnikov, P.
M., Pashchenko, V. Z., Seifullina, N. Kh., Grishanova, N. P., and
Rubin, A. B. (2016) Temperature dependence of protein fluorescence in
Rb. sphaeroides reaction centers frozen to 80 K in the dark or on the
actinic light as the indicator of protein conformational dynamics,
Dokl. Biochem. Biophys., 467, 105-109.
16.Knox, P. P., Lukashev, E. P., Korvatovskii, B.
N., Gorokhov, V. V., Pashchenko, V. Z., Seifullina, N. Kh., Grishanova,
N. P., and Rubin, A. B. (2016) A comparison of the temperature
dependence of charge recombination in the ion-radical pair
P870+QA– and tryptophan
fluorescence in the photosynthetic reaction centers of Rhodobacter
sphaeroides, Biophysics, 61, 923-930.
17.Ross, J. A., and Jameson, D. M. (2008)
Time-resolved methods in biophysics. 8. Frequency domain fluorometry:
applications to intrinsic protein fluorescence, Photochem.
Photobiol. Sci., 7, 1301-1312.
18.Olsson, C., Jansson, H., and Swenson, J. (2016)
The role of trehalose for the stabilization of proteins, J. Phys.
Chem. B, 120, 4723-4731.
19.Adams, P. D., Chen, Y., Ma, K., Zagorski, M. G.,
Sonnichsen, F. D., McLaughlin, M. L., and Barkley, M. D. (2002)
Intramolecular quenching of tryptophan fluorescence by the peptide bond
in cyclic hexapeptides, J. Am. Chem. Soc., 124,
9278-9286.
20.Hayward, B. J., and Henry, B. B. (1976)
Experimental manifestations of the local mode description of high
energy polyatomic overtone spectra, Chem. Phys., 12,
387-396.
21.Tarasevich, B. N. (2012) IR-Spectra of Major
Classes of Organic Compounds. Reference Materials [in Russian],
MSU, Moscow.
22.Medvedev, E. S., and Osherov, V. I. (1983)
Theory of Non-radiative Transitions in Multiatom Molecules [in
Russian], Nauka, Moscow.
23.Emanuel, N. M., and Kuzmin, M. G. (1985)
Experimental Techniques in Chemical Kinetics [in
Russian], MSU, Moscow.