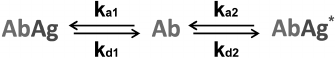REVIEW: Mathematical Modeling of Bioassays
D. V. Sotnikov, A. V. Zherdev, and B. B. Dzantiev*
Bach Institute of Biochemistry, Research Center for Biotechnology, Russian Academy of Sciences, 119071 Moscow, Russia; E-mail: dzantiev@inbi.ras.ru, zherdev@inbi.ras.ru* To whom correspondence should be addressed.
Received September 11, 2017; Revision received September 19, 2017
The high affinity and specificity of biological receptors determine the demand for and the intensive development of analytical systems based on use of these receptors. Therefore, theoretical concepts of the mechanisms of these systems, quantitative parameters of their reactions, and relationships between their characteristics and ligand–receptor interactions have become extremely important. Many mathematical models describing different bioassay formats have been proposed. However, there is almost no information on the comparative characteristics of these models, their assumptions, and predictive insights. In this review we suggested a set of criteria to classify various bioassays and reviewed classical and contemporary publications on these bioassays with special emphasis on immunochemical analysis systems as the most common and in-demand techniques. The possibilities of analytical and numerical modeling are discussed, as well as estimations of the minimum concentrations that may be detected in bioassays and recommendations for the choice of assay conditions.
KEY WORDS: bioassay, immunoassay, analytical modeling, numerical modeling, theoretical detection limitDOI: 10.1134/S0006297917130119
Abbreviations: ELISA, enzyme-linked immunosorbent assay; ICA, immunochromatographic assay; PFIA, polarization fluorescent immunoassay; PCR, polymerase chain reaction; RIA, radioimmunoassay; RU, resonance units; SPR, surface plasmon resonance.
Detection methods based on the interaction of a substance of interest
with biological receptor molecules are called bioassays. Receptors can
be antibodies, enzymes, cell surface receptors, non-antibody
combinatorial compounds, oligonucleotides, peptides, lectins, etc. [1]. The ability of certain biological molecules to
specifically recognize target molecules makes them an ideal tool for
detecting target compounds in complex mixtures. Bioassays have found
broad application for routine laboratory analysis in medical and
veterinary diagnostics, environmental monitoring, biosafety, and many
other areas, as well as research tools to obtain new information on the
structure and properties of various molecules and molecular
complexes.
Two approaches have been found to be most promising in the development of bioassays. The first one is incorporation of various labels into the reagents with their following detection in the complexes formed during the assay. In many cases, the use of labels reduces detection limits of the method by several orders of magnitude. The second approach is immobilization of one of the reagents on the support with the possibility of further separation (wash-off) of the unreacted molecules, such as excess reagents, sample components, etc. Although methods that do not use labels or separation of reactants (immunoprecipitation, immunoagglutination, immunoelectrophoresis, etc.) are well known and have for a long time dominated the field of bioassays, currently these methods occupy a very limited niche. Since the principles of such method have been described in detail in many publications [2-6], we will not discuss them in our article.
Mathematical modeling is an integral part of the theoretical basis of any assay. Development and analysis of a mathematical model help to understand the mechanisms of processes that occur in the system, to explain various negative phenomena and to eliminate them. Mathematical models also have a predictive function and allow to evaluate the impact of various factors and parameters on the assay results without long laborious experiments. Although any theoretical model only partially corresponds to a real process, the model reflects the general principles of the system functioning. As a rule, a model of an assay is considered valid if it can be used the calculate the concentration of the detected complex from the initially specified parameters, such as reagent concentrations, interaction constants, time, etc. The established theoretical relationship between the initial analyte concentration and the concentration of the detected complex describes the assay calibration curve. Based on this relationship, it is possible to calculate the optimal reagent ratios and the duration of the process stages, as well as other assay parameters, e.g., detection limit, dynamic range, etc.
Mathematical modeling of a system can be carried out by finding exact solution to equations that describe the system in a general form (analytical modeling) or by finding an approximate solution for specific parameter values via step-by-step numerical calculations (numerical modeling). Modern computer technologies enable numerical modeling of multicomponent systems, while taking into account multiple parallel reactions, polyvalent interactions, diffusion, and other processes [7-14]. However, non-numerical (analytical) solutions are preferable for understanding the functioning of assays. Although such solutions exist only for the simplest models, they are actively used to develop recommendations for improving bioassay protocols [15, 16].
This review focuses on the models of various bioassays described in the literature and methods for achieving the optimal analytical characteristics that follow from these models. Various existing models and their evolution are discussed. We also systemized and unified the descriptions of bioassay systems proposed in other publications.
DIVERSITY OF BIOASSAY FORMATS
The number of different biochemical assays proposed at different times is very large, and the assays are classified in different ways. The situation becomes even more complicated because depending on the manner of classification and the scope of use, the same method can be named differently. Various bioassay formats and general principles of their development have been described in many reviews [17-22].
Let us consider one of the possible classifications of bioassay formats using immunoassay as an example.
All immunoassay methods can be subdivided based on the structure of the assayed antigen. The first group consists of monovalent antigens interacting with only one antibody molecule; the second group includes polyvalent antigens capable of binding with several antibody molecules. The first group is formed by low molecular weight compounds: pesticides, antibiotics, peptides, etc. Biopolymers and corpuscular structures (viruses, cells) are typical polyvalent antigens.
In assay systems for monovalent antigens, formation of the antigen–antibody complexes is not registered directly1. Instead, they implement competitive assay schemes for which two options are possible: antibody labeling with antigen immobilization or antigen labeling with antibody immobilization.
1Direct registration is possible, but it forfeits basic advantages of modern assay systems: the use of labels to identify immune complexes and the use of solid supports to separate them.
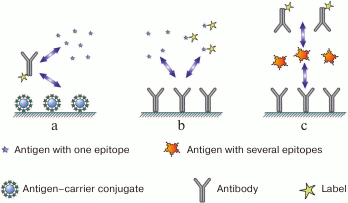
In the first case (Fig. 1a), two types of antigens compete for the binding sites in the antibody: free antigen, the content of which in the sample is to be measured, and immobilized antigen introduced into the system in a certain chosen amount. After interaction, antibodies bound to the immobilized antigen remain on the support, and the remaining antibodies (including those that reacted with the antigen in the solution) are washed off. The higher the content of free antigen in the sample, the lesser amount of the label binds to the carrier and can be detected after the assay is completed (i.e., inverse relationship between the analyte concentration and the recorded signal).
Fig. 1. Main immunoassay formats (see the text for description).
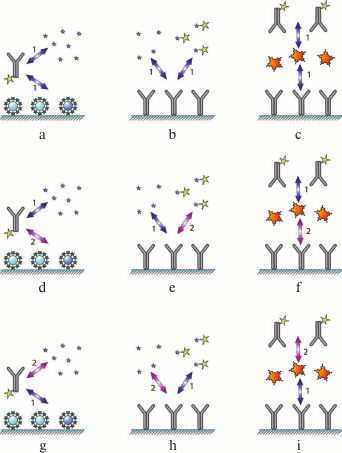
As the interactions in the system involve two reactions, the assay can be carried out by changing the order of the immunoreagent interactions: (i) simultaneous incubation of the antibody and both types of antigen (Fig. 2a); (ii) preincubation of the antibody and the antigen of interest, followed by the interaction of the antibody and immobilized antigen (Fig. 2d), and
(iii) interaction of the immobilized antigen with the labeled antibody, followed by the addition of the antigen of interest to release some of the bound antibodies to the solution (Fig. 2g).
Fig. 2. Classification of immunoassay formats. The designations are identical to those in Fig. 1. Numbers 1 and 2 indicate the order of reagent addition (see the text for the explanation).
By varying the duration of each stage, the range of detectable antigen concentrations can be shifted.
In the second case (Fig. 1b), the assay involves interactions between the immobilized antibody and two types of the antigen: labeled antigen at a known concentration and unlabeled antigen that is present in the sample in an unknown (to be determined) concentration. Both types of antigen compete for the binding sites of immobilized antibodies. As a result, the ratio between the labeled and unlabeled antigens in the complex with the antibody reflects the initial ratio between these two antigen types in the solution. The more unlabeled antigen is present in the sample, the less amount of labeled antigen binds to the immobilized antibody (inverse relationship between the analyte concentration and the registered signal).
This type of assay can be also carried out in three ways: (i) simultaneous addition of the labeled and unlabeled antigens to the immobilized antibody (Fig. 2b); (ii) interaction of the antibody with the unlabeled antigen, followed by the addition of the labeled antigen (Fig. 2e); (iii) or preincubation of the antibody with the labeled antigen, followed by the addition of the unlabeled antigen (Fig. 2h); as a result, the labeled antigen will be displaced by the unlabeled antigen from its complex with the antibody.
Let us now consider assay formats for polyvalent antigens. In principle, they can employ competitive assay as well; however, formation of triple, or the so-called sandwich complexes (immobilized antibody–antigen–labeled antibody) (Fig. 1c), provides greater sensitivity. Binding to the excess amount of immobilized antibody concentrates the antigen, and provides very high sensitivity of the assay [23]. Theoretically, such system is capable of detecting even a single antigen molecule bound to the antibody, because a decrease in the background signal and increase in the sensitivity of the label detection can potentially reduce the antigen detection threshold infinitely [24]. In contrast to the competitive assay, the relationship between the analyte concentration and the registered signal (the amount of the bound label) in the sandwich assay is direct.
This approach can also be implemented in three different ways by changing the sequence of interactions between the antigen and the antibody: (i) simultaneous incubation of the antigen with the labeled and unlabeled antibodies (Fig. 2c); (ii) interaction of the antigen first with the labeled antibody and then with the unlabeled antibody (Fig. 2f); (iii) interaction of the antigen first with the unlabeled antibody and then with the labeled antibody (Fig. 2i).
The sandwich assay can be used for monovalent antigens as well. Such efforts were summarized in a recent review [25]. However, antibody binding to the antibody complex with a low-molecular-weight compound requires development of special reagents, which is time-consuming work and significantly limits the use of this assay format, even that in some cases, it exhibits very high sensitivity [26].
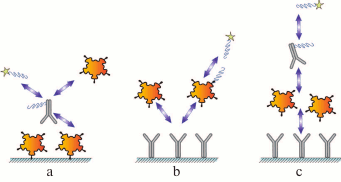
Each assay scheme described above can be subdivided into two groups based on the method for label incorporation: (i) direct labeling of the antibody or the antigen via formation of a chemical covalent bond or by adsorption; (ii) label in incorporated into additional modules that interact (in a separate reaction or at one of the assay stages) with the assay components, e.g., anti-species antibodies or high-affinity pairs of reagents, such as biotin–(strept)avidin and barnase–barstar (Fig. 3).
Fig. 3. Immunoassay formats with indirect labeling: a) competitive assay with labeled antibody; b) competitive assay with labeled antigen; c) sandwich assay.
Based on the way the label is register after the assay is completed, each of the formats mentioned above can subdividing into two groups: (i) measuring the label immobilized on a support as part of the immune complex or (ii) measuring the unbound label.
Such classification results in 36 (3 × 3 × 2 × 2) potentially feasible formats of heterogeneous immunoassay that can be described according to a single scheme.
The methods of homogeneous assay, with no separation of the reagents or use of solid supports, form a separate group of immunoassays. In these methods, antibody--antigen binding is detected based on various indirect parameters: (i) change in the rotation speed of the labeled antigen after its interaction with the antibody (polarization fluoroimmunoassay) [27, 28]; (ii) modulation of the marker fluorescence after formation of the immune complexes, such as FRET assay, “quenchbodies”, and “flashbodies” [29-32]; (iii) decrease in the activity of the enzyme label due to the difficulties in accessing the substrate after formation of the immune complexes [33, 34]; (iv) antibody-modulated assembly of oligomeric enzymes resulting in a change in their catalytic activity [35]; (v) changes in the optical, acoustic, and other parameters due to the immune complex formation of [36-38], etc.
In addition, there are the so-called pseudohomogeneous assay formats in which immunoreagent attached to a carrier, but the antibody–antigen interactions take place in a solution, and only after that, the carrier together with the bound immune complexes is separated from other components of the reaction mixture. The most widely used variant of pseudohomogeneous assay is one in which the magnetic particles are used as a dispersed carrier and then separated using an external magnetic field [39, 40]. Assay systems that use charged polymers precipitated by counterions, heat-sensitive polymers, and other compounds as carriers have also been described [41-44].
We should also mention bioassays in which antibodies are analytes and antigens act as receptor molecules, such as serodiagnosis and identification of specific immunoglobulins (antibodies) in the blood used to diagnose infections and allergies [45]. In such systems, the antigen is usually immobilized on a solid support, and the label is conjugated with the reagents that bind to immunoglobulins (anti-species antibodies, protein A from Staphylococcus aureus, protein G from Streptococcus spp., or other reagents) [46, 47]. If specific immunoglobulins are present in the test sample, detectable complexes antigen–specific immunoglobulins–labeled immunoglobulin-binding protein are formed on the support.
Label-free assay systems, as well as systems that register the complex formation from the label incorporation in it, have a substantially simpler order of interactions, the theoretical description of which could be approximated by the “antigen + antibody = complex” bimolecular reaction. Piezoelectric immunosensors, immunosensors based on the registration of surface plasmon resonance, and a number of other biosensors are based on this principle [48-52].
Therefore, when considering mathematical models of bioassays, it is necessary to take into account what detectable complexes are formed and in what order these complexes are formed in bioassays.
LABELS USED IN BIOASSAYS
There are several key periods in the history of bioassay development, during which considerable progress has been achieved due to the appearance of new labels for detecting specific complexes. For example, in 1960 Yalow and Berson proposed the use of the radioactive isotope 131I to detect immune complexes [53]. The radioimmunoassay (RIA) significantly increased the sensitivity and accuracy of measurements and turned out to be a versatile approach that could be used for detection of a wide variety of compounds. The importance of this invention was acknowledged by the 1977 Nobel Prize in Physiology and Medicine awarded to R. S. Yalow.
Despite the indisputable advantages of RIA, its application has been limited due to the complexity of working with isotopes. Therefore, enzymes have been introduced as alternative labels. The methods for antibody labeling with enzymes and registration of enzymatic activity had already been partially developed for immunohistochemical applications. However, numerous further advances were required to ensure high yields of immunoreagent--enzyme conjugates and their stability [54-57]. As a result, as early as the 1980s, kits and semiautomatic and automatic devices for enzyme-linked immunosorbent assay (ELISA) became commercially available. At about the same time, devices for polarization fluorescence immunoassay (PFIA) were successfully commercialized, and automatic systems for high-throughput testing were introduced [58].
During the 1990s, there was a sharp expansion in the production of at-home diagnostic test systems based on the immunochromatographic assay (ICA). In these test systems, the assay has been reduced to the contact between the analyzed sample and the test strip covered with immunoreagents. The movement of the liquid under the influence of capillary forces along the test strip initiates all the necessary reactions and results in the staining of certain zones of the test strip. The main markers in immunochromatography are gold nanoparticles and colored latex particles [59, 60].
Active interest in nanotechnology at the beginning of the 21st century led to the examination of a wide variety of nanoparticles as a replacement for traditional labels in existing assay formats and resulted in the development of new bioassays and biosensors. Immunoanalytical applications have been suggested for different classes of nanoparticles, such as colloidal gold particles of different shapes, colloidal silver, carbon nanoparticles, magnetic nanoparticles, quantum dots, upconverting fluorophores, infrared labels, liposomes, silicon nanoparticles, etc. [61, 62]. As a rule, when a new label is proposed for application in bioassays, it is common to consider the analytical characteristics of the assay that could be achieved with this label in comparison to the traditional assay. However, massive methodical solutions are updated relatively slowly. Not every improvement in assay sensitivity described in the literature becomes the basis for the assay modification in practice.
The modern diversity of bioassay labels is presented in the article by Zelenakova et al. [63]: insoluble particles (erythrocytes, latex granules, graphite particles, sols of metals and dyes, e.g., of gold and Luminous Red G), radionuclides (125I, 131I, 3H), enzymes (horseradish peroxidase, alkaline phosphatase), electron-scattering substances, bacteriophages, fluorescent dyes, chemiluminescent and bioluminescent compounds, liposomes, prosthetic groups; enzyme substrates, and enzyme modulators.
Such diversity stipulates for the criteria that would aid in drawing conclusions about the competitive potential of a new label before or even instead of its experimental evaluation. These criteria have to summarize the intrinsic characteristics of the label without being related to a particular assay format or analyzed compound, so that the label could be appropriately described before being used in the development of an assay system, thereby significantly reducing the labor cost of the studies.
In our opinion, the following parameters should be taken into account when evaluating a label:
These three parameters determine the coefficients for recalculating the label characteristics for a particular assay system, and therefore, they are very important for quantitative descriptions.
However, a number of other important criteria exist that are related to the practical aspects of the label application and can prevent the use of otherwise promising labels. These criteria include [60]:
Modern bioassays are not limited to the use of labels with low detection limits. Many assays involve additional amplification processes that increase the number of label molecules (particles) bound to the immune complex or used for the signal registration [64-66]. For example, integration of antibody-based detection of an analyte with subsequent amplification of the signal from the oligonucleotide marker by standard polymerase chain reaction (PCR) is particularly interesting. This immuno-PCR method drastically reduces the immunoassay detection limits and can register the minimum number of molecules in the order of tens or hundreds [67, 68]. Supersensitive assay systems based on the detection of single immune complexes have being actively developed, although at present they require sophisticated instrumentation [69, 70].
KEY CONCEPTS AND PROCESSES FOR MODELING BIOASSAY SYSTEMS
When modeling a bioassay, a number of factors should be taken into account in addition to the assay scheme: (i) whether equilibrium or non-equilibrium conditions of interaction are considered; (ii) whether reactions for forming specific complexes are considered reversible or irreversible; (iii) whether diffusion-dependent processes are taken into account; (iv) whether the model reflects the possibility of bi- and polyvalent interactions in the analyte–receptor complexes, etc.
Although any bioassay is based on the interaction of an analyzed compound (analyte) with a biomolecule specifically binding this analyte (receptor) and it models should describe the kinetic properties of this interaction, the above questions could be answered differently, depending on the assay conditions. Accordingly, different theoretical apparatuses could be chosen to describe a bioassay.
Quantitative description of diffusion. As noted above, in most modern bioassays, detectable immune complexes are formed on a solid support. Therefore, theoretical description of these assays cannot be limited to solving relatively simple problems of interaction in a solution and should accommodate the diffusion of one of the reactants toward the support on which another reactant is immobilized and the corresponding inhomogeneity in the distribution of reagent concentrations in the reaction volume. Consequently, the proposed model should include either description of the diffusion-dependent processes in explicit form or justified recommendations for the use of certain simplifying assumptions that would take into account specific features of this particular assay system.
Diffusion-limited reactions are typical for heterogeneous systems [71] and/or systems where the interaction takes place in a viscous medium, e.g., precipitation reaction in a gel [3]. However, only a few of proposed bioassay mathematical models consider diffusion processes. The general questions of diffusion-dependent processes in assays were discussed in the classical papers of Stenberg and Nygren [72-74], but, with a few exceptions [75-77], have not been elaborated further. Most authors of the assay mathematical models introduce conditional concentrations in a volume for immobilized reagents and then discuss the classical patterns of homogeneous reactions.
The change in the concentration of the diffusing component (C) over time at the point with coordinates (x, y, z) is determined by Fick’s second law:
The value of diffusion coefficient D determines the amount of material passing through a unit of surface per unit of time [78, 79]. The value of D is measured in m2/s and depends on the properties of both the solvent and the solute. In the approximation for the Brownian spherical particle, the diffusion coefficient is expressed as:
where k is the Boltzmann constant, T is the temperature of the medium, µ is the viscosity coefficient, and r is the particle radius.
In assay modeling, Fick’s second law is used not only to describe the rate of reactant movement to the receptor surface [71] but also to characterize the reactant distribution in the flow in flow-through systems. For example, Qian and Bau [80] used Fick’s second law to account for the diffusion of reactants in the stream of a liquid sample in the mathematical description of immunochromatography in the sandwich format. According to the Qian and Bau’s model, the change in the label (colloidal gold) concentration at a point with the coordinate x (the direction of the x axis coincides with the direction of the fluid flow) is described as follows:
where A is the detected compound (analyte), P is the analyte-binding sites on the label, R is the receptor in the capture zone for analyte binding, PA is the analyte complex with the label, RPA is the analyte complex with the label and the receptor in the capture zone, x is the coordinate of the position on the test strip, Fn is the rate of the n-th complex formation, U is the fluid flow rate, and Dp is the label diffusion coefficient.
The expression U·d[concentration of reagent]/dx in Eq. (3) reflects the change in the concentration of P at a point with coordinate x resulting from the fluid flow that shifts positions of all dissolved molecules and particles. The expression Dp·d2[concentration of reagent]/dx2 reflects the change in the concentration of P at a point with coordinate x resulting from the diffusion processes described by Fick’s second law.
Qian and Bau’s model assumes that the properties of the assay system do not differ in the y and z directions, which makes it possible to use the one-dimensional form of Eq. (1). This approximation is completely justified, considering small transverse sizes (5-15 µm) of pores in the membranes used in immunochromatographic assays.
In recent years, numerous papers have been published that deal with various aspects of diffusion-dependent processes in bioassays, such as effects of rotational diffusion on the antigen transport [81], the use of fractal models to describe microheterogeneous processes on the biosensor surfaces [82], the choice of the geometry of binding microzones to minimize the diffusion-dependent processes [83, 84], the design of microfluidic systems with rapid achievement of the chemical equilibrium [85], the elimination of diffusion in pseudohomogeneous systems using nanoparticles [86] and polymers [87], etc.
Unlike flow-through bioassay systems, including immunochromatographic tests, most other assay formats employ regimes in which reagents have time to redistribute in the volume. When the reagents are incubated for tens of minutes in milliliter or submilliliter volumes, diffusion can be neglected. In assays with shorter incubation times, special procedures are used to accelerate diffusion in the near-surface layer, such as mixing, ultrasound treatment, etc. [88-93].
Quantitative description of chemical transformations. The quantitative description of chemical transformations in assay systems not limited by diffusion is based on the main postulate of chemical kinetics, i.e., the law of mass action. For the analyte–receptor reaction in its simplest case of monovalent binding (A + R ↔ AR), the law of mass action provides the differential equation for the rates of changes in the reagent and complex concentrations [94]:
where ka and kd are kinetic association and dissociation constants of the AR complex, respectively.
Taking into account that [A] + [AR] = [A]0 and [R] + [AR] = [R]0, where the subscript 0 denotes initial concentrations of the reagents, Eq. (4) could be reduced to the form with a single variable [AR]:
Equation (5) has a rigorous analytical solution, which is the function:
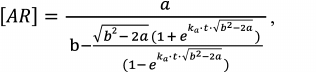 (6)
(6)where a = 2[A]0[R]0, b = [A]0 + [R]0 + kd/ka.
This exact solution is almost never used in the models described in published literature; instead, approximate solutions are applied. When the kinetics of affinity complexes formation is described, two main approximations are adopted as a rule: (i) equilibrium conditions of the interaction; (ii) the irreversibility of the binding reaction.
The equilibrium state is defined by the condition that all reaction rates equal zero, from which follows the expression:
where Ka is the equilibrium association constant, or the affinity constant.
This is a very rough approximation for express bioassays, in which reagents are incubated for several minutes only, although it is used in practice [80, 95, 96]. When characterizing kinetic systems, the approximation that the binding reaction is irreversible is better justified, as the receptor molecules used in bioassays usually exhibit high affinity for the detected compound. For example, antibodies rarely have kinetic dissociation constant greater than 10–4 s–1 [97], i.e., less than 6% of the formed immune complex would dissociate within 10 min. Therefore, dissociation in the kinetic assay system can be neglected.
The product formation in the bimolecular irreversible reaction A + R → AR is described by Eq. (8) [98]:
Note that Eq. (8) is the limiting case of Eq. (6) for kd → 0.
Theoretical limits of parameters of the antigen–antibody reaction. The traditionally mentioned advantage of antibodies is a high affinity of antibody–antigen complex that allows detection of antigens in extremely low concentrations. However, the affinity of the immune complex is limited by the nature of the immune response induction, which imposes limitations on the detection limit of immunoassays.
The maximum association rate constant (ka) for the interaction of antibodies with protein antigens is determined by the rate of diffusion of the protein molecules in solution; it is of the order of 106 M–1·s–1 [99]. The dissociation rate constant of the complex (kd) can be increased by the antibody selection in vivo [100, 101], but only to a certain limit. According to the affinity ceiling hypothesis [101-103], further antigen-driven selection of clones already secreting high-affinity antibodies occurs less efficiently. This is because for antibodies with kd = 10–4 s–1, the half-life of the antigen complex with the B cell receptor is almost 2 h, which is several times greater than the duration of the endocytosis of antibody complex with the B cell receptor (about 8.5 min). Further increase in the half-life of the complex no longer promotes proliferation of B cells. Therefore, during the secondary immune response, the values of the equilibrium association constant for the anti-antigen immunoglobulins G (IgG) are within the range of 107-1010 M–1.
The limitations on the selection of high-affinity clones described above do not exclude the possibility that for some antigens, a significantly higher degree of complementarity with the antigen-binding site in the antibody and a correspondingly higher association constant can be achieved. Non-dissociating antigen–antibody complexes were described in [104]. In this study, antibodies with an infinite affinity for the chelate complex of (S)-benzyl-EDTA with indium were obtained as a result of a directed antibody design. Similar effects were observed for the interaction between the antigen and the antibody–metal ion complex in [105].
Experimental evaluation of interactions parameters in bioassay. Although finding the analytical solution in a general form for a system of equations is the best way of theoretically describing a bioassay, characterization of a bioassay requires the knowledge of quantitative parameters of the analyte–receptor interactions, first of all, kinetic and equilibrium reaction constants. Knowing these parameters allows to evaluate the validity of assumptions used in the model development and, if necessary, to resort to numerical modeling.
The methods for measuring association and dissociation constants of biomolecular complexes are very diverse [106]. For example, equilibrium dialysis and elution of reagents from affinity columns have been widely used for this purpose [107]. A theoretical apparatus for the calculation of association constants in capillary electrophoresis experiments has been developed [108-110]. The methods based on fluorescence and fluorescence polarization measurements enabled direct rapid characterization of the ligand–receptor interactions in a solution [111-113]. ELISA is another popular approach to measuring the constants, although it also represents a type of bioassay that is constantly developed, as well as used for characterization of reagents in the development of other assays. Classical recommendations on this subject have been proposed Friquet and Djavadi-Ohaniance et al. in [114-116]. The details of processing of experimental data and the choice of the most valid procedures for calculations are discussed in a number of later works [117-121].
Despite all this diversity, generally accepted gold standard for measuring and comparing the constants of intermolecular interactions is the biosensor assay based on the registration of surface plasmon resonance (SPR). Let us consider in detail the principle of the operation and data processing for the Biacore biosensor system, as the most widely used among optical sensor systems [122].
The experimental procedure for the intermolecular interaction characterization in the Biacore system includes:
1) immobilization of one of the interacting components on the chip surface;
2) passing a solution containing the second component of the interacting pair over the chip surface, with simultaneous registration of the interaction;
3) ceasing the inflow of the second component into the cell and registering the dissociation of the formed complex;
4) regeneration of the chip surface with solutions that disturb the ligand–receptor complex but do not damage the immobilized component;
5) repeating stages 2 through 4 with other preparations that react with the immobilized component.
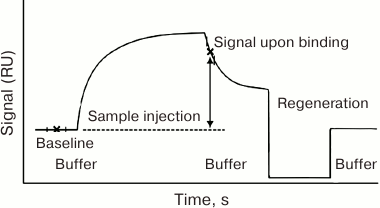
The dependence of the device response (the SPR value) on time is called the sensogram [123]. Its principal general form is shown in Fig. 4.
Fig. 4. General form of the sensogram registered in the Biacore system. RU, resonance units.
The sensogram contains all the data necessary to calculate kinetic and equilibrium parameters of the complex formation [124-127]. The simplest model that allows to calculate the constants from the sensogram assumes the equilibrium conditions and excludes diffusion-dependent processes from consideration [125-127].
Association stage. Taking into account the equilibrium approximation, the association stage is described by Eq. (4), where the time derivatives of concentrations equal zero:
Since the concentration of active receptor molecules on the sensor surface ([R]) is usually unknown, it is more convenient to consider the degree of surface filling (θ) instead. The θ value is the RU/RUmax ratio, where RU is the signal value (minus the background) and RUmax is the maximum signal value (minus the background) when all the receptor molecules are bound to the surface. The concentrations of free and bound receptor molecules can be expressed through the initial concentration of the receptor [R]0 and θ: [R] = (1 θ)[R]0 and [AR] = θ [R]0 [128].
Because at the association stage, the analyte constantly enters the reaction zone with the fluid flow and, according to the assumptions, is immediately uniformly mixed, its concentration above the sensor surface can be considered constant, i.e. [A] ≈ [A]0. The increase in the analyte concentration near the surface resulting from its specific binding can also be neglected, as the analyte amount at the sensor surface is much smaller than in the volume; therefore, we can assume that the average analyte concentration due to the interaction with the receptor varies insignificantly. The higher the fluid flow rate, the more accurate this approximation would be. Thus, Eq. (9) can be rewritten as follows:
Equation (11) describes the signal on the equilibrium association constant and the concentration of the analyte entering the cell. Assuming the equilibrium state, RU values closest to the equilibrium values (the upper plateau of the association part of the sensogram) should be substituted into the equation. The interaction constant could be calculated using solutions with known concentrations of the analyte.
Dissociation stage. Dissociation of the immune complex is a monomolecular reaction, and its rate depends only on the kinetic dissociation constant. In a flow-through system, dissociation can be considered irreversible, since dissociation products are washed away from the reaction zone, and new complexes cannot form because of the analyte absence in the washing fluid. Therefore, the dependence of the dissociated complex content (D) on the time of dissociation (t) is determined by the kinetic equation of the irreversible monomolecular reaction:
The portion of the dissociated complex is calculated as D = 1 – RU/RU0, where RU0 is the signal value (minus the background) at the moment when dissociation begins, and RU is the signal value (minus the background) at the moment of time t.
Bivalence of antibodies and its role in immunoassay. An important feature of antibodies that distinguishes them from other receptor molecules is the presence of multiple binding sites for the analyte. Immunoglobulins G, that are most commonly used in assays, have two antigen-binding sites, whereas immunoglobulins M have 10 binding sites1. If identical epitopes on the antigen surface are located at a sufficient distance from each other, this antigen can bind not one but two antibodies. Such polyvalent antigens are viral particles, bacterial cells, biopolymers with degenerate structure, some oligomeric proteins, and synthetic antigen–carrier conjugates.
1 Fragmented antibodies from certain animals (the so-called nanobodies), recombinant antibodies with only one antigen-binding site, and specially prepared antibody fragments are monovalent.
The bivalent antibody–antigen interaction results in a number of consequences important for the bioassay evaluation: (i) formation of a mixture of immune complexes of different composition and affinity between antibodies and polyvalent antigens; (ii) significantly lesser probability of dissociation of the antigen–antibody complexes with the bivalent binding.
In competitive immunoassays, polyvalent interactions of antibodies with a standard antigen (usually a synthetic analyte–carrier conjugate) impair the detection sensitivity, because complexes with a monovalent antigen from the analyzed sample are less stable than those with a polyvalent antigen. Therefore, the “worsening” of the standard antigen by reducing the analyte content in it would increase the assay sensitivity [129-131].
Various aspects of the polyvalent interactions in bioassays have been discussed in [132-140]. Shiau [141] analyzed the immune complex formation in a system consisting of two types of monoclonal antibodies and a bivalent antigen with two identical epitopes. The author did not consider the possibility of the cyclic complex formation, as well as of the cooperativity effect, and studied only the average molecular weight of linear antigen–antibody complexes. Joshi [142] used the statistical-mechanical theory to model the dependence of the formation of complexes of different composition on the antibody affinity. Joshi considered two systems: interactions between monoclonal antibodies and an antigen of a known valency with identical determinants, and a more complicated case where the properties of the binding sites of the antibodies and the antigens differed. A theoretical study on the effect of clusterization of receptors in various configurations on the kinetic parameters of immune interactions was presented by van Opheusden et al. [143]. Hlavacek et al. [144] proposed a model for the multivalent ligand–receptor binding, that took into account the shielding of several receptors by a ligand (typical for viruses and multivalent protein antigens) and studied the effect of this factor on the kinetic and equilibrium parameters of the reaction. The properties of assay systems using antigen-loaded liposomes were examined by Hendrickson et al. [145].
An attempt to take into account polyvalent interactions without overcomplicating calculations techniques was made by the authors of [11], who used in their model the so-called nodal analysis (NODE). This method considers the kinetics of each reaction of a multicomponent process in a separate node within a short time interval and then constructs the iterative process that encompasses the whole reaction period. The model could be made more complex by introducing additional reactions and, accordingly, the nodes for the calculations.
In general, the authors of studies on bivalent immune interactions note the need for considering the differences between the affinity of a simple interaction between the antigen epitope and the antibody binding and affinity of an average immune complex that reflects poly- and monovalent interactions for a given pair of reagents.
The ratio between the equilibrium association constants for bi- and monovalent antibody–antigen interactions can be up to two orders of magnitude [146, 147]. It depends on the antibody and the antigen used and reflects the mechanism of interaction between the antibody active site and the corresponding antigen epitope, the mobility of the immunoglobulin molecule segments, and the distance between antigenic determinants and their orientation on the surface of the polyvalent antigen. Crothers and Metzger [148] calculated association constants for the two active sites of the antibody based on experimentally determined values of the monovalent interaction.
MODELS OF VARIOUS BIOASSAYS
Competitive immunoassay. The principle of the classical competitive immunoassay with a labeled antigen (Fig. 1b) is a simultaneous interaction of antibodies (Ab) with an antigen (Ag) and its labeled analog (Ag*) [149]. Accordingly, there are two reactions in the system.
* Ab + Ag ↔ AbAg
* Ab + Ag* ↔ AbAg*
The reactions are characterized by the kinetic association constants ka1 and ka2 and kinetic dissociation constants kd1 and kd2. In the simplest case, all binding sites in the antibodies are assumed to be identical. All the transformations in this system are described by the scheme shown in Fig. 5.
Fig. 5. Reactions in the competitive immunoassay with a labeled antigen (see the text for explanations).
Let us construct the calibration curve for this system, i.e., the dependence of the detected signal (the amount of bound label) on the analyte concentration in the tested sample. The examination of this function allows theoretical investigation of the influence of various parameters on the analytical characteristics of the method.
Based on the law of mass action, we can write a system of differential equations:
The system should be supplemented with equations expressing the law of conservation of mass:
Here and below, the index 0 denotes the initial concentrations of the reactants. Note that [Ab] is the total concentration of the binding sites in the antibodies, because antibodies are polyvalent.
Several variants of the analytical solution from the system of Eqs. (13)-(18) have been described in published literature. As a rule, the approximation of equilibrium conditions is used [2, 149] that allows to convert Eqs. (13)-(15) in a system of algebraic equations:
Expressing Eqs. (14) and (15) through the equilibrium association constants results in:
For simplicity, in the first competitive assay models the affinities of the antibodies to the antigen and its labeled analog were assumed to be identical, i.e., Ka1 = Ka2 = Ka [2, 150]. In this case:
Expression (23) means that if the constants are equal, then the content of the free labeled antigen is equal to the content of the free unlabeled antigen, because
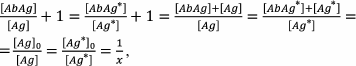 (24)
(24)where x is the proportion of the free antigen (labeled or unlabeled).
If the proportions of the free labeled and unlabeled antigens are equal, then the proportions of the bound labeled and unlabeled antigens are equal as well:
Adding Eqs. (19) and (20), after the transformations, we obtain:
Considering that [AbAg] = y[Ag]0; [AbAg*] = y[Ag*]0; [Ag] = (1 – y)[Ag]0; [Ag*] = (1 – y)[Ag*]0; [Ab] = [Ab]0 – ([AbAg] + [AbAg*]) = [Ab]0 – y([Ag]0 + [Ag*]0), Eq. (26) can be rewritten as:
Equation (27) can be found in the literature in various forms; for example, in [150], the equation is transformed to:
In fact, this is a quadratic equation that unites the proportion of the bound antigen, the initial concentrations of the binding sites of the antibodies, the concentrations of the labeled and unlabeled antigen, and the interaction constant (complex dissociation constant):
The solution of the quadratic Eq. (29) describes in general form the assay calibration curve:
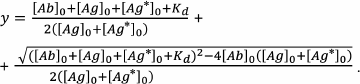 (30)
(30)Later, the competitive assay models were considered for the case when the antibody affinities to the labeled and unlabeled antigens differ [22, 151, 152]. Such system is described by the cubic equation derived from Eqs. (16)-(22):
where:
a = Kd1 + Kd2 + [Ag]0 + [Ag*]0 – [Ab]0,
b = Kd2([Ag]0 – [Ab]0) + Kd1([Ag*]0 – [Ab]0) + Kd2Kd1,
c = –Kd2Kd1 [Ab]0.
Using the trigonometric formulas, the solution of Eq. (31) is:
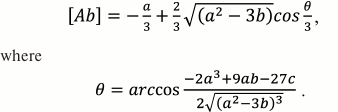 (32)
(32)Having found [Ab], we can write the formulas for [AbAg] and [AbAg*]:
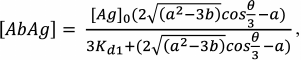 (33)
(33)
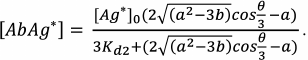 (34)
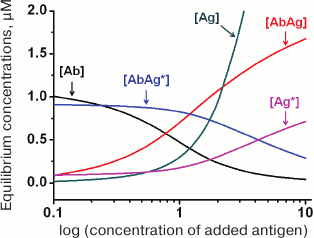
(34)An example of the equilibrium concentrations of components in a competitive assay system that were calculated from Eqs. (32)-(34) while keeping in mind Eqs. (16)-(18) is shown in Fig. 6. Of particular interest is the dependence of [AbAg*] on the concentration of the added antigen, because it is essentially a calibration curve of the assay. Analysis of this curve will allow evaluation of potential analytical characteristics of the method and the influence of the initial parameters on them.
Fig. 6. Calculated equilibrium concentrations of components in a competitive assay system. Parameters: [Ab]0 = 2 µM; [Ag*]0 = 1 µM; Ka1 = 5 µM–1; Ka2 = 10 µM–1.
In the alternative competitive assay format, the antigen is immobilized, and the labeled reagent is an antibody that simultaneously interacts with the immobilized antigen and the free antigen in the solution (competitor) (Fig. 2a). However, the kinetic model presented above is equally suitable for describing this variant of the assay (importantly, in both systems the diffusion of the reagents to the surface is not considered), except that some of the designations must be changed: Ab is the labeled antibodies, and Ag* is the immobilized antigen. The detected complex is AbAg*, as in the first case.
Another competitive assay format is the sequential saturation method, in which the antibodies first interact with the antigen to be detected (reaction (1)), and then, after washing-off, with the labeled antigen (reaction (2)). Rodbard et al. [153] showed the that this method is much more sensitive than the procedure involving simultaneous incubation of the antibodies with the unlabeled and labeled antigens. Based on the analysis of the mathematical model of this system, Dzantiev and Yuriev formulated recommendations for improving the assay characteristics [154]. In the sequential saturation method, the assay parameters are determined by the reaction with the antigen to be detected. The reaction with the labeled antigen plays an auxiliary role by allowing the number of free binding sites to be registered. When the strict proportionality [AbAg*] = C*[Ab] is achieved, the calibration curve in the normalized coordinates should completely coincide with the antigen titration curve. In reality, this proportionality might be violated; therefore, assay optimization should be selection of conditions under which the calibration curve corresponds best to the titration curve. The authors of [154] also showed that in order to fulfill this requirement, the incubation time with the labeled antigen should equal to approximately 0.1/kd1. A good correlation between the experimental and calculated data has been shown for the insulin ELISA as an example.
If in order to characterize the extent of reaction with a detected antigen, we introduce the coefficient n (the proportion of the antibody binding sites filled with the antigen after equilibrium is established), then the following formulas are valid:
n[Ab]0 = [AbAg] = [Ab]0 – [Ab], n = 1 – [Ab]/[Ab]0.
Using the expressions for the equilibrium association constant, [AbAg] = Ka1[Ab][Ag] = Ka1([Ab]0 – [AbAg])([Ag]0 – [AbAg]), we can write:
n[Ab]0 = Ka1([Ab]0 – n[Ab]0)([Ag]0 – n[Ab]0). (35)
From here, we can obtain an expression that relates the proportion of the filled binding sites in antibodies to the association constant and the initial concentrations of the reagents:
Equations (30), (34), and (36) describe the calibration curves of various competitive assay formats, predict the behavior of systems with varying concentrations of reagents and association constants, and establish theoretical limits for detection by this method, ranges of detectable concentrations and other assay parameters (see section “Theoretical evaluations of the potential of bioassay systems”).
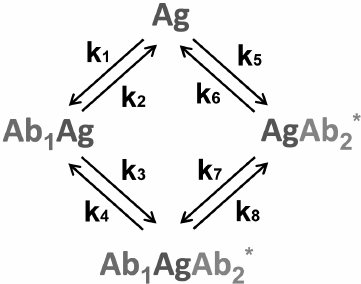
Sandwich immunoassay. In the sandwich immunoassay, detected antigen has two epitopes for binding two antibodies: one of these antibodies is immobilized on the support, while the other antibody is labeled. Ab1 is the first antibody; Ab2* is the labeled second antibody, and Ag is the detected antigen. The classical sandwich assays with the immobilization of the first antibody (RIA and ELISA) involve seven steps: 1) immobilization of the Ab1 antibody; 2) washing off unbound antibodies; 3) incubation with the antigen Ag, i.e., Ab1 + Ag ↔ Ab1Ag (1A) reaction with the association constant k1 and dissociation constant k2; 4) washing off unbound Ag; 5) incubation with the labeled Ab2* antibody, i.e., Ab1Ag + Ab2* ↔ Ab1AgAb2* (1B) reaction with the association constant k3 and dissociation constant k4; 6) washing off unbound labeled antibodies; 7) measurement of the signal proportional to the concentration of the [Ab1AgAb2*] complex.
Ideally, only Ab1 molecules and Ab1Ag complexes remain on the surface after stage 4, after which the Ab1Ag complex dissociates with the formation of free antigen molecules. Therefore, two additional reactions take place during stage 5: Ab2* + Ag ↔ Ab2*Ag (1C) and Ab1 + AgAb2* ↔ Ab1AgAb2* (1D) with the association constants k5 and k7 and dissociation constants k6 and k8, respectively.
The complete scheme of the reactions in the sandwich immunoassay is shown in Fig. 7.
Fig. 7. Reactions in the sandwich immunoassay (see the text for explanations).
Rodbard and Feldman [155] analyzed these reactions based on the assumption that the first antibody binds to the support irreversibly, and the unbound reagents are completely washed away at each stage.
The reactions in the sandwich immunoassay could be described by a system of differential equations:
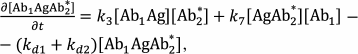 (37)
(37)
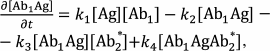 (38)
(38)
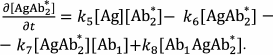 (39)
(39)Three additional algebraic equations follow from the law of conservation of mass:
In total, a system of six equations with six unknowns, [Ag], [Ab1], [Ab2*], [Ab1Ag], [AgAb2*], and [Ab1AgAb2*], was obtained; p, q1, and q2 are the total concentrations of the bound and free Ag, Ab1, and Ab2, respectively.
The authors solved this system with numerical methods or analytically with the approximation of equilibrium conditions [155]. The analytical solution after substitution of R = [Ab1Ag]/[Ag] after reaction (1A) provides the following equation:
Taking into account tall the accepted assumptions, the initial conditions for the following reactions are determined by the equations:
The solution to Eq. (43) with respect to R gives the following expression:
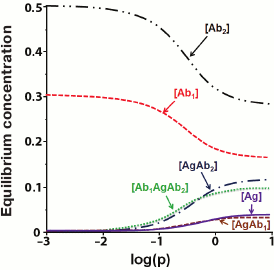
After R is found, the concentrations of the remaining components of the system could be calculated. Figure 8 shows the results of numerical modeling as dependences of the concentrations of different products of interaction at the last stage of the assay.
Fig. 8. Calculated equilibrium concentrations of components in the sandwich assay. Parameters: q1 = 3/K1 = 0.3; q2 = 0.5; k1 = k7 = 5; k3 = k5 = 10; k2 = k4 = k6 = k8 = 1 (according to [155]).
The presented model shows that when the concentration of the added analyte increases, the concentration of the detectable complex [Ab1AgAb2*] should increase monotonically. However, some experimental data demonstrate that at high analyte concentrations, the dependence can be reversed [156]. This phenomenon is called the hook effect [157, 158]. Because of it, Rodbard and Feldman modified their model and showed that the hook effect occurs when subpopulations of antibodies with different affinities are present or when the antigen is not completely washed away after the reaction with antibodies [159].
Other mechanisms underlying the hook effect have been established as well. For example, the hook effect can be observed when labeled antibody competes with the unlabeled one for the binding sites on the antigen, but only if the concentration of labeled antibody is lower than the concentration of the unlabeled antibody [160]. The hook effect has also been described for the one-stage sandwich assay, in which labeled and unlabeled antibodies react with the antigen simultaneously (Fig. 2c) [161]. Zherdev and Dzantiev showed in a microplate ELISA, that the hook effect can result from the desorption of the first antibody during the subsequent assay stages. They also demonstrated that in order to minimize the influence of desorption and dissociation effects, it is important to carry out incubation with the second antibody as quickly as possible and not longer than for 1/kd [162].
There are a number of additional approaches for bioassay modeling and theoretical investigation of the influence of experimental conditions on the assay characteristics. Among the promising mathematical description techniques, fractal analysis is of particular interest. Sadana et al. used fractal analysis for examining different types of bioassays in [163-165]. Theoretical evaluation of the temperature influence on the ELISA characteristics was presented by Muller in [166]. Software tools for optimizing competitive ELISA were provided by Sittampalam et al. in [167]; similar approaches were developed by Tsoi et al. in [168]. Theoretical approaches to selecting conditions for expanding the working range of ELISA were discussed by Ohmura et al. [169]. Model and Healy reviewed the methods for optimization of assay conditions with specific attention to the procedure sensitivity and cost in [170].
THEORETICAL EVALUATION OF THE BIOASSAY POTENTIAL
Development of the bioassay model provides the possibility for the theoretical evaluation of the limiting analytical characteristics of the method. The main bioassay parameters are the detection limit, specificity, and duration [171, 172]. Most attention has been given to the calculation of the theoretical limits of analyte detection in various immunoassay formats [173-176].
Because the analyte–receptor complexes are detected in one way or another in all biochemical immunoassay, the equilibrium and kinetic constants of analyte–receptor binding directly affect the assay parameters. However, the analyte detection limit is also influenced by the sensitivity of the label detection, experimental errors, and nonspecific interactions in the system.
The detection limit and the quantitative measurement limit are frequently confused, as it was pointed out by C. F. Woolley et al. [23]. The detection limit is the amount of the analyte that gives a signal that reliably exceeds the background, whereas the quantitative measurement limit corresponds to the amount of the analyte that is measured with a certain accuracy, which the researcher considers sufficient. Therefore, the concept of the detection limit has a qualitative character and reflects only the presence of the analyte in a sample. These issues are especially important in the context of rapidly developing methods for a single molecule measurement, which have become possible due to the appearance of ultrasensitive measuring systems that can detect the activity of a single label molecule (particle) [177-179]. In practice, detection of a single molecule in a sample means only a high probability of the presence of this molecule in a sample. The limit of quantitative measurements in such systems is much higher than single molecules.
Let us consider in more detail the theoretical evaluations of the limiting analytical characteristics of various bioassays and their relationship with the parameters of affinity interaction.
Jackson–Ekins criterion. The theoretical detection limits for noncompetitive and competitive immunoassays methods and their relationship with antibodies characteristics were the first time established by Jackson and Ekins [176].
They showed that in competitive immunoassays, experimental errors and antibody affinity determine the detection limit, as expressed by the following ratio:
σmin,0 = CV0/Ka, (48)
where σmin,0 is the theoretical minimum of the standard deviation of the system response at zero analyte concentration, and CV0 is the variation coefficient of the system response at zero analyte concentration.
Jackson and Ekins also found that for immunoassays with a direct correlation between the analyte concentration and the detected signal value, the detection limit can potentially be reduced by several orders of magnitude. However, for noncompetitive methods, nonspecific interactions in the system can also significantly influence the detection limit in addition to experimental errors and antibody affinity, which is described by the expression:
σmin,0 = Kn*CV/Ka, (49)
where σmin,0 is the theoretical minimum of the standard deviation of the system response at zero analyte concentration, CV is the relative error of the system response at zero analyte concentration, and Kn is the relative value of nonspecific binding. For example, if the antibody association constant is 1012 M–1, CV is 1%, and the level of nonspecific binding is 1%, the theoretical minimum of the standard deviation is 10–16 M.
Expressions (48) and (49) were derived based on the assumption that the label has an unlimited activity and does not restrict the detection limit.
Taylor et al. [150] used the Jackson–Ekins model to calculate the detection limits for different Ka and CV0 values in the competitive assay using the standard requirement that the minimum detected signal should be three times the standard deviation of the baseline signal (table). As follows from the data presented, it is theoretically possible to achieve a detection limit in the femtomolar concentration range, if the antibodies used have with the affinity constant of 1012 M–1. Based on the Jackson–Ekins model, it can be assumed that at the same antibody affinity, the detection limit of the noncompetitive assay might be lower than the detection limit of the competitive method by a value that is inversely proportional to the nonspecific binding level (Kn). This implies a possibility of a potentially unlimited lowering of the detection limit with decreasing Kn. In practice, if the nonspecific binding is eliminated, the detection limit will be limited by the label detection sensitivity.
Theoretical detection limits (DL) for competitive immunoassay,
calculated according to the model by Jackson and Ekins in [150]
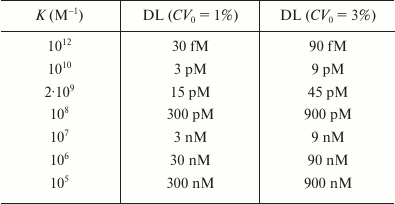
The model by Jackson and Ekins significantly influenced the development of bioassays by defining the boundaries of the methods that use receptors and markers. Although a number of authors discuss how to overcome the limitations on the assay sensitivity imposed by this model, it is not a question of refuting it, but rather developing new approaches to detecting immune complexes, including methods for a single molecule detection [23, 177, 180-182].
Relationship between the parameters of affinity interactions and assay characteristics. The process for optimization of a biochemical assay, which includes multiple components and stages, usually requires a large number of laborious experiments [167, 183]. To simplify this process, a number of optimization schemes have been developed, such as the Doehlert matrix [184], the Box-Behnken design [185], the Taguchi design [186, 187], and other [168, 188, 189]. However, these schemes do not allow an a priori assessment of maximum achievable assay parameters.
There are very few publications on the correlation between the affinity constants and assay characteristics. Rodbard and Lewald [190] were the first to propose an algorithm for constructing the RIA calibration curves in order to predict the detection limits. The theoretical model of RIA proposed by Ezan et al. [191] based on the law of mass action gives the dependence:
where C is the unlabeled antigen concentration, K is the antibody affinity, [Ag*] is the initial concentration of the labeled antigen, b0 is the ratio of the antigen–antibody complex concentration to the total antigen concentration in the absence of unlabeled antigen, and bc is the same ratio in the presence of unlabeled antigen.
Within the framework of this model, Ezan et al. showed the decisive effect of the parameter bc on the achievable detection limit:
where t is the Student’s criterion, s is the standard deviation of the parameter b0, n is the number of measurements for one antigen concentration, n0 is the number of determinations of parameter b0, and bDL is the parameter bc value for the unlabeled antigen concentration corresponding to the detection limit.
The actual detection limit (CDL), taking into account Eq. (50), is calculated by the formula:
This expression shows how to vary the assay conditions in order to achieve the minimum detection limit. For example, when working with high-affinity antibodies (Ka > 1010 M–1), the concentration of the labeled antigen should be reduced. If the antibody affinity is much lower, then the amount of the labeled antigen should be increased to reduce the measurement error.
Similar correlations between the affinity constants and assay characteristics have been analyzed for other methods, such as the RIA [181], capillary immunoelectrophoresis [150], ELISA [192, 193], and immunochromatography [80, 95].
The influence of the measurement accuracy on the immunoassay characteristics was discussed in [194]. Theoretical evaluation of the immunoassay detection limits and working ranges was presented [192]. The model by Hayashi et al. [194] takes into account the relative standard deviations (ρT) for the following parameters: errors for pipetting antigen (ρA), antigen–enzyme conjugate (ρG), antibody (ρB), and enzyme substrate (ρS) and the differences in the absorption in different microplate wells (σW):
where A is the analyte concentration, and G is IC50.
Based on the quantitative parameters of the affinity complex formation, the proposed model makes it possible to establish the optimal conditions for competitive immunoassays.
Dzantiev and Yuriev analyzed the relationship between the parameters of affinity interaction and the characteristics of competitive assays with sequential saturation [146]. They showed that if [Ab]0 < 1/Ka1, then the detection limit is determined mainly by the value of 1/Ka1; and if [Ab]0 > 1/Ka1, then the detection limit is determined by the value of [Ab]0. Therefore, the use of antibodies with an initial concentration of ~1/Ka1 would be optimal. An increase in the antibody concentration from two orders of magnitude (0.1/K – 10/K) at [Ab]0 << 1/Ka1, to one order of magnitude (0.1[Ab]0 – [Ab]0) at [Ab]0 >> 1/Ka1 narrows the dynamic range of the detected concentrations. However, when the antibody concentration decreases, the relative error in antigen determination increases due to the decrease of the calibration curve slope in the dynamic range area.
FLOW-THROUGH BIOASSAYS
Coming after traditional immunoassay methods, such as RIA, ELISA, etc., flow-through bioassays have now established their place in the laboratory practice. However, open heterogeneous flow-through require transition to the models of a much greater complexity. A number of works have been devoted to the theoretical description of flow-through biosensors [195-199]. The proposed models take into account the reaction system geometry and the effect of diffusion transport on the kinetics of binding of dissolved ligands to the immobilized receptors [200]. Despite the complexity of the flow-through heterogeneous systems, models have been developed based on the minimum number of assumptions that provide general analytical description of the interactions in these systems and can be used for predicting the properties of their functioning.
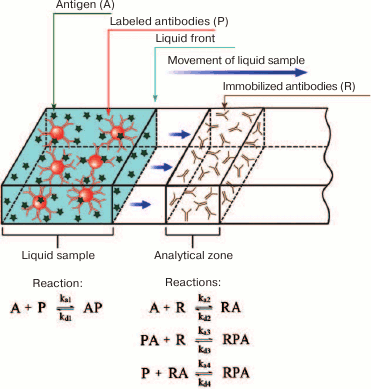
Below, we present the results of mathematical modeling of ICA systems, which are the most popular now among the lateral-flow immunoassays due to the simplicity of their use and interpretation of the results.
An important feature of the membrane-based systems is the difference in the properties of immunoreagents in solution and immobilized immunoreagents. The use of effective constants determined for one type of the assay in an alternative assay is rather conventional; the same is true for the amount of immobilized immunoreagents in terms of the volume concentration.
In 2003-2004, Qian and Bau developed for the first time the analytical (non-numerical) models for the ICA in the sandwich and competitive formats [80, 95]. A simplified scheme for the sandwich ICA used for its modeling is shown in Fig. 9. When the liquid front moves along the test strip membrane, the antigen first interacts with the labeled antibody. After the liquid front reaches the capture zone, the antibody–antigen complex interacts with the secondary antibody immobilized in the capture zone, resulting in the formation of the detected triple complex.
Fig. 9. A simplified scheme of the sandwich ICA used for the model development.
To account for the kinetics of the complex formation, diffusion, and liquid flow in the test strip, a system of equations is introduced:
where A is the detectable compound (analyte), P is the sites for analyte binding on the label, R is the receptor in the capture zone for analyte binding, PA is the analyte complex with the label, RA is the analyte complex with the receptor, RPA is the label–analyte–receptor complex in the capture zone, x is the coordinate of the position on the test strip (the system is considered one-dimensional), Fn is the rate of the n-th complex formation, U is the liquid flow rate, and Dp is the diffusion coefficient.
Expressions in a form of U·d[reagent concentration]/dx reflect the change in the concentration of the corresponding reagent (A, P, or PA) at a point with coordinate x due to the liquid flow, while expressions in a form of Dp·d2[reagent concentration]/dx2 reflect the change in the concentration of the corresponding reagent (A, P, or PA) at a point with coordinate x due to diffusion. Complexes containing R are formed only in the capture zone; therefore, their concentration does not depend on the flow and diffusion.
The accepted assumption [80, 95, 201] that the distribution of components in a flow obeys the Fick’s second law does not take into account a number of factors, such as nonspecific interactions with membranes, desorption, the possibility of preliminary mixing of reagents, etc. Therefore, by introducing the parameters that reflect diffusion processes, Qian and Bau [95] actually analyzed a simplified version of the equations for reagents uniformly distributed in the volume.
Qian and Bau further analyzed a system of equations describing the formation of AP, AR, and APR complexes:
where kai is the kinetic association constant of the i-th reaction, and kdi is the kinetic dissociation constant of the i-th reaction.
This system of equations cannot be solved in the general form. Therefore, the authors made the assumption on the equilibrium conditions, which allowed to calculate the concentration of the RPA complex in the capture zone (which is proportional to the color development intensity) according to the following equations:
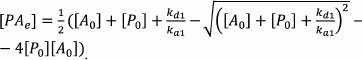 (63)
(63)The index e denotes the equilibrium concentration, and the index 0 denotes the initial concentration.
The same authors proposed the mathematical models for description of competitive ICA. The models have been developed for two cases:
1) The analyte binds to the antibody immobilized on the membrane, thereby blocking the interaction of the immobilized antibodies with the labeled conjugate. The higher the amount of the analyte, the fewer free binding sites on the membrane for the conjugate, and the lower the signal level (Fig. 2b).
2) The analyte binds to the conjugate of the labeled antibodies and interferes with the interaction of the conjugate with the antigen molecules immobilized on the membrane. The higher the amount of the analyte, the fewer binding sites on the conjugate that are available for binding in the capture zone (Fig. 2d).
Remember that this dependence was derived under the assumption of the equilibrium conditions of immunochromatography. However, according to data by Ragavendar and Anmol [96], at parameters typical for real immunoreagents (A0 = 10–8; P0 = 10–8; ka = 106; kd = 10–3) and a fluid flow rate of 0.5 mm/s, the reactions on the test strip will approach the equilibrium only if the capture zone is located about 12 cm from the position of the sample application. This distance significantly exceeds the size of the working membrane of a standard immunochromatographic test (2.5 cm). Therefore, in reality, immunochromatographic reactions take place under nonequilibrium conditions and require a more complex mathematical description.
The published models of ICA that take into account nonequilibrium processes use numerical approaches to calculate the kinetics of the immune interactions [202-204].
To describe the immune complex formation in the capture and control zones of the test strip, Krishnamoorthy et al. [205] proposed a model that takes into account diffusion in membrane pores in combination with a system of differential equations that reflect the interactions in solution. The model views the flow as a two-phase mixture: a liquid phase that partially or completely fills the pores and air that occupies the remaining space. The authors of the paper assumed that the flow is two-dimensional, and there is no loss of reagents from the membrane surface due to evaporation. If the volume is averaged, the flow density can be regarded constant, and the dissipation due to the viscosity can be neglected. The position of the liquid front is proportional to the diffusion constant, which depends on the pore size, viscosity, and surface tension. This system has been numerically characterized for different variants of reagent flow (water, colloidal gold in water, and colloidal gold conjugate with BSA in water) across membranes with different pore sizes (from 4 to 20 µm). The model describes the influence of membrane porosity and the position of the binding lines on the number of immune complexes that form. The results of experimental and theoretical studies [205] show that the flow rate in an immunochromatographic system decreases with the distance from the starting line, i.e., position of the binding zone significantly affects the sensitivity of the assay. The flow rate moderately increases with the increasing pore size. This reduces the incubation time and, correspondingly, the intensity of the registered staining. These correlations were confirmed by Berli and Kler in their analysis of the sandwich ICA model [15]. Hence, the sensitivity of ICA is influenced by time, concentration of reagents, pore size, and position of the capture zone.
ICA for determination of specific antibodies has many features that require separate theoretical consideration. Immunochromatographic serodiagnosis is similar to the sandwich ICA. The distinction of the serodiagnostic assay is that the detected reagent is the antibody, while the antigen is used as a specific receptor. An important feature of the serodiagnostic ICA is that at the first stage of the assay, the conjugate of the label with the immunoglobulin-binding reagent interacts with all immunoglobulins in the sample, while in the capture zone, only specific immunoglobulins, which comprise a small fraction of all blood immunoglobulins, interact with the antigen. Sotnikov et al. [16] proposed an analytical model for such system. The authors showed that in order to lower the detection limit for specific antibodies in ICA, it is necessary to use the highest possible reagent concentrations for antibody binding and to dilute the sample at least ten times before performing the assay.
In all the above-mentioned works, the conjugates of the labels with receptor molecules were presented as a set of analyte-binding sites distributed in a reaction volume. These models do not take into account the dimensional parameters of the label particles and the composition of their conjugates. An attempt to evaluate the influence of these parameters on the characteristics of the sandwich ICA was undertaken by Liu et al. in a recent study [206]. According to their conclusions, conjugates that have about 30 analyte-binding sites on one label particle are best suited for the use in sandwich ICA.
The presented review of the published literature confirms that there is still a need for theoretical description of bioassays. Although it is impossible to measure all quantitative parameters of the reagents used in each known assay or to predict theoretically the value of the detected signal, general descriptions of bioassays (primarily based on numerical solutions describing their functioning in a general form) are in high demand. Having established the principles of the system behavior, it is possible to formulate general recommendations for choosing reagent concentrations and duration of the assay stages, to identify factors that limit the maximum sensitivity, and to adapt assay systems for solving specific practical problems. Theoretical models can determine the full potential of various assay formats, evaluate the effectiveness of the proposed solutions for signal amplification, and shorten the duration of the interaction in an assay. Using the theoretical approach will make the process of assay development less labor-consuming and allow comparison of different assays.
Acknowledgments
The authors thank A. N. Berlina (Centre for Biotechnology, Russian Academy of Sciences) for the preparation of Figs. 1-3.
This work was supported by the Russian Science Foundation (project No. 14-14-01131).
REFERENCES
1.Dzantiev, B. B., and Zherdev, A. V. (2010)
Immunoanalytical methods, in Problems of Analytical Chemistry,
Vol. 12. Biochemical Assay Methods (Dzantiev, B. B., ed.) [ in
Russian], Nauka, Moscow, pp. 303-332.
2.Merrill, S. J. (1998) Computational models in
immunological methods: an historical review, J. Immunol.
Methods, 216, 69-92.
3.Fedorov, A. A., Kurochkin, V. E., Martynov, A. I.,
and Petrov, R. V. (2010) Theoretical and experimental investigation of
immunoprecipitation pattern formation in gel medium, J. Theor.
Biol., 264, 37-44.
4.Goldberg, R. J. (1952) A theory of
antibody–antigen reactions. I. Theory for reactions of
multivalent antigen with bivalent and univalent antibody, J. Am.
Chem. Soc., 74, 5715-5725.
5.Steensgaard, J., Liu, B. M., Cline, G. B., and
Moller, N. P. (1977) The properties of immune complex-forming systems.
A new theoretical approach, Immunology, 32, 445-456.
6.Zhang, P., and Wang, H. J. (2010) Statistics and
thermodynamics in the growth of antigen–antibody complexes,
Chinese J. Physics, 48, 277-293.
7.Svitel, J., Boukari, H., Van Ryk, D., Willson, R.
C., and Schuck, P. (2007) Probing the functional heterogeneity of
surface binding sites by analysis of experimental binding traces and
the effect of mass transport limitation, Biophys. J., 92,
1742-1758.
8.Svitel, J., Balbo, A., Mariuzza, R. A., Gonzales,
N. R., and Schuck, P. (2003) Combined affinity and rate constant
distributions of ligand populations from experimental surface binding
kinetics and equilibria, Biophys. J., 84, 4062-4077.
9.Lebedev, K., Mafe, S., and Stroeve, P. (2006)
Convection, diffusion and reaction in a surface-based biosensor:
modeling of cooperativity and binding site competition on the surface
and in the hydrogel, J. Colloid Interface Sci., 296,
527-537.
10.Hu, G., Gao, Y., and Li, D. (2007) Modeling
micropatterned antigen–antibody binding kinetics in a
microfluidic chip, Biosens. Bioelectron., 22,
1403-1409.
11.Ylander, P. J., and Hanninen, P. (2010) Modelling
of multi-component immunoassay kinetics – a new node-based method
for simulation of complex assays, Biophys. Chem., 151,
105-110.
12.Jomeh, S., and Hoorfar, M. (2010) Numerical
modeling of mass transport in microfluidic biomolecule-capturing
devices equipped with reactive surfaces, Chem. Eng. J.,
165, 668-677.
13.Friedrich, D., Please, C., and Melvin, T. (2008)
Optimization of analyte transport in integrated microfluidic affinity
sensors for the quantification of low levels of analyte, Sens. Act.
B Chem., 131, 323-332.
14.Botkin, N. D., and Turova, V. L. (2004)
Mathematical models of a biosensor, Appl. Math. Model.,
28, 573-589.
15.Berli, C. L., and Kler, P. A. (2016) A
quantitative model for lateral flow assays, Microfluidics
Nanofluidics, 20, 104.
16.Sotnikov, D. V., Zherdev, A. V., and Dzantiev, B.
B. (2017) Mathematical model of serodiagnostic immunochromatographic
assay, Anal. Chem., 89, 4419-4427.
17.Goryacheva, I. Y. (2016) Formats of rapid
immunotests – current-day formats, perspectives, pros and cons,
Comprehensive Anal. Chem., 72, 33-78.
18.Bilitewski, U. (2006) Protein-sensing assay
formats and devices, Anal. Chim. Acta, 568, 232-247.
19.Sajid, M., Kawde, A. N., and Daud, M. (2015)
Designs, formats and applications of lateral flow assay: a literature
review, J. Saudi Chem. Soc., 19, 689-705.
20.Thevenot, D. R., Toth, K., Durst, R. A., and
Wilson, G. S. (2001) Electrochemical biosensors: recommended
definitions and classification, Biosens. Bioelectron.,
16, 121-131.
21.Sharma, S., Byrne, H., and O’Kennedy, R. J.
(2016) Antibodies and antibody-derived analytical biosensors, Essays
Biochem., 60, 9-18.
22.Egorov, A. M., Osipov, A. P., Dzantiev, B. B.,
and Gavrilova, E. M. (1991) Theory and Practice of Enzyme
Immunoassay [in Russian], Vysshaya Shkola, Moscow, p. 288.
23.Woolley, C. F., Hayes, M. A., Mahanti, P.,
Gilman, S. D., and Taylor, T. (2015) Theoretical limitations of
quantification for noncompetitive sandwich immunoassays, Anal.
Bioanal. Chem., 407, 8605-8615.
24.Chang, L., Rissin, D. M., Fournier, D. R., Piech,
T., Patel, P. P., Wilson, D. H., and Duffy, D. C. (2012) Single
molecule enzyme-linked immunosorbent assays: theoretical
considerations, J. Immunol. Methods, 378, 102-115.
25.Fan, M., and He, J. (2012) Recent progress in
noncompetitive hapten immunoassays: a review, in Trends in
Immunolabelled and Related Techniques (Abuelzein, E., ed.), InTech,
Rijeka, pp. 53-66.
26.Ueda, H. (2002) Open sandwich immunoassay: a
novel immunoassay approach based on the interchain interaction of an
antibody variable region, J. Biosci. Bioeng., 94,
614-619.
27.Smith, D. S., and Eremin, S. A. (2008)
Fluorescence polarization immunoassays and related methods for simple,
high-throughput screening of small molecules, Anal. Bioanal.
Chem., 391, 1499-1507.
28.Goulko, A. A., Zhao, Q., Guthrie, J. W., Zou, H.,
and Le, X. C. (2008) Fluorescence polarization: recent bioanalytical
applications, pitfalls, and future trends, in Standardization and
Quality Assurance in Fluorescence Measurements I (Wolfbeis, O. S.,
ed.), Springer, Leipzig, pp. 303-322.
29.Shi, J., Tian, F., Lyu, J., and Yang, M. (2015)
Nanoparticle based fluorescence resonance energy transfer (FRET) for
biosensing applications, J. Mater. Chem. B, 3,
6989-7005.
30.Lee, J. Y., Kim, J. S., Park, J. C., and Nam, Y.
S. (2016) Protein–quantum dot nanohybrids for bioanalytical
applications, Nanomed. Nanobiotechnol., 8, 178-190.
31.Abe, R., Ohashi, H., Iijima, I., Ihara, M.,
Takagi, H., Hohsaka, T., and Ueda, H. (2011)
“Quenchbodies”: quench-based antibody probes that show
antigen-dependent fluorescence, J. Am. Chem. Soc., 133,
17386-17394.
32.Wongso, D., Dong, J., Ueda, H., and Kitaguchi, T.
(2017) Flashbody: a next generation Fluobody with fluorescence
intensity enhanced by antigen binding, Anal. Chem., 89,
6719-6725.
33.Zherdev, A. V., Dzantiev, B. B., and Trubaceva,
J. N. (1997) Homogeneous enzyme immunoassay for pyrethroid pesticides
and their derivatives using bacillary alpha-amylase as label, Anal.
Chim. Acta, 347, 131-138.
34.Chiu, M. L., Lai, D., and Monbouquette, H. G.
(2011) An influenza hemagglutinin A peptide assay based on the
enzyme-multiplied immunoassay technique, J. Immunoassay
Immunochem., 32, 1-17.
35.Curtis, E. G., and Patel, J. A. (1978) Enzyme
multiplied immunoassay technique: a review, Crit. Rev. Clin. Lab.
Sci., 9, 303-320.
36.Polshchitsin, A. A., Nekrasov, V. M.,
Zakovryashin, V. S., Yakovleva, G. E., Maltsev, V. P., Yurkin, M. A.,
and Chernyshev, A. V. (2017) Kinetic turbidimetry of patchy colloids
aggregation: latex particles immunoagglutination, Colloids Surf. A
Physicochem. Eng. Aspects, 516, 72-79.
37.Priev, A., Sarvazyan, A., Dzantiev, B., Zherdev,
A., and Cherednikova, T. (1990) Alterations in adiabatic
compressibility of monoclonal and polyclonal antibodies induced by
interactions with antigens, Mol. Biol. (Moscow), 24,
514-521.
38.Sheikh, S., Blaszykowski, C., and Thompson, M.
(2008) Acoustic wave-based detection in bioanalytical chemistry:
competition for surface plasmon resonance? Anal. Lett.,
41, 2525-2538.
39.Schrittwieser, S., Pelaz, B., Parak, W. J.,
Lentijo-Mozo, S., Soulantica, K., Dieckhoff, J., Ludwig, F., Guenther,
A., Tschope, A., and Schotter, J. (2016) Homogeneous biosensing based
on magnetic particle labels, Sensors, 16, 828.
40.Urusov, A. E., Petrakova, A. V., Zherdev, A. V.,
and Dzantiev, B. B. (2017) Application of magnetic nanoparticles in
immunoassay, Nanotechnol. Rus., 12, (in press).
41.Uehara, N., Numanami, Y., Oba, T., Onishi, N.,
and Xie, X. (2015) Thermal-induced immuno-nephelometry using gold
nanoparticles conjugated with a thermoresponsive polymer for the
detection of avidin, Anal. Sci., 31, 495-501.
42.Dzantiev, B. B., Zherdev, A. V., and Yazynina, E.
V. (2002) Application of water-soluble polymers and their complexes for
immunoanalytical purposes, in Smart Polymers for Bioseparation and
Bioprocessing (Mattiasson, B., and Galaev, I. Yu., eds.), Taylor
Fransis, London-N.Y., pp. 207-229.
43.Englebienne, P., and Weiland, M. (1996) Synthesis
of water-soluble carboxylic and acetic acid-substituted poly
(thiophenes) and the application of their photochemical properties in
homogeneous competitive immunoassays, Chem. Commun., 14,
1651-1652.
44.Chen, J. P., and Huffman, A. S. (1990)
Polymer–protein conjugates: II. Affinity precipitation separation
of human immunogammaglobulin by a
poly(N-isopropylacrylamide)–protein A conjugate,
Biomaterials, 11, 631-634.
45.Ryan, K. J., and Ray, C. G. (2004) Sherris
Medical Microbiology, McGraw-Hill Education, pp. 247-249.
46.Chareonsirisuthigul, T., Khositnithikul, R.,
Intaramat, A., Inkomlue, R., Sriwanichrak, K., Piromsontikorn, S.,
Kitiwanwanich, S., Lowhnoo, T., Yingyong, W., Chaiprasert, A., and
Banyong, R. (2013) Performance comparison of immunodiffusion,
enzyme-linked immunosorbent assay, immunochromatography and
hemagglutination for serodiagnosis of human pythiosis, Diagn.
Microbiol. Infect. Dis., 76, 42-45.
47.Abebe, F., Holm‐Hansen, C., Wiker, H. G.,
and Bjune, G. (2007) Progress in serodiagnosis of Mycobacterium
tuberculosis infection, Scand. J. Immunol., 66,
176-191.
48.Mauriz, E., Garcia-Fernandez, M. C., and Lechuga,
L. M. (2016) Towards the design of universal immunosurfaces for
SPR-based assays: a review, Trends Anal. Chem., 79,
191-198.
49.Homola, J. (2008) Surface plasmon resonance
sensors for detection of chemical and biological species, Chem.
Rev., 108, 462-493.
50.Yuan, Y., Panwar, N., Yap, S. H. K., Wu, Q.,
Zeng, S., Xu, J., Tjin, S. C., Song, J., Qu, J., and Yong, K. T. (2017)
SERS-based ultrasensitive sensing platform: an insight into design and
practical applications, Coord. Chem. Rev., 337, 1-33.
51.Qiao, X., Zhang, X., Tian, Y., and Meng, Y.
(2016) Progresses on the theory and application of quartz crystal
microbalance, Appl. Phys. Rev., 3, 031106.
52.Rich, R. L., and Myszka, D. G. (2010) Grading the
commercial optical biosensor literature – Class of 2008:
“The Mighty Binders”, J. Mol. Recognit., 23,
1-64.
53.Yalow, R. S., and Berson, S. A. (1960)
Immunoassay of endogenous plasma insulin in man, J. Clin.
Invest., 39, 1157-1175.
54.Avrameas, S., and Uriel, J. (1966) Method of
antigen and antibody labelling with enzymes and its immunodiffusion
application, C. R. Acad. Sci. Hebd. Seances Acad. Sci. D,
262, 2543-2545.
55.Nakane, P. K., and Pierce, G. B., Jr. (1967)
Enzyme-labeled antibodies for the light and electron microscopic
localization of tissue antigens, J. Cell Biol., 33,
307-318.
56.Engvall, E., and Perlman, P. (1971) Enzyme-linked
immunosorbent assay (ELISA). Quantitative assay of immunoglobulin G,
Immunochemistry, 8, 871-874.
57.Van Weeman, B. K., and Schuurs, A. H. (1975) The
influence of heterologous combinations of antiserum and enzyme-labeled
estrogen on the characteristics of estrogen enzyme-immunoassays,
Immunochemistry, 12, 667-670.
58.Jolley, M. E., Stroupe, S. D., Schwenzer, K. S.,
Wang, C. J., Lu-Steffes, M., Hill, H. D., Popeika, S. R., Holen, J. T.,
and Kelso, D. M. (1981) Fluorescence polarization immunoassay. III. An
automated system for therapeutic drug determination, Clin.
Chem., 27, 1575-1579.
59.Posthuma-Trumpie, G. A., Korf, J., and Van
Amerongen, A. (2009) Lateral flow (immuno) assay: its strengths,
weaknesses, opportunities and threats. A literature survey, Anal.
Bioanal. Chem., 393, 569-582.
60.Dzantiev, B. B., Byzova, N. A., Urusov, A. E.,
and Zherdev, A. V. (2014) Immunochromatographic methods in food
analysis, Trends Anal. Chem., 55, 81-93.
61.Goryacheva, I. Y., Lenain, P., and De Saeger, S.
(2013) Nanosized labels for rapid immunotests, Trends Anal.
Chem., 46, 30-43.
62.Huang, X., Aguilar, Z. P., Xu, H., Lai, W., and
Xiong, Y. (2016) Membrane-based lateral flow immunochromatographic
strip with nanoparticles as reporters for detection: a review,
Biosens. Bioelectron., 75, 166-180.
63.Ronald, A., and Stimson, W. H. (1998) The
evolution of immunoassay technology, Parasitology, 117,
S13-S27.
64.Shan, S., Lai, W., Xiong, Y., Wei, H., and Xu, H.
(2015) Novel strategies to enhance lateral flow immunoassay sensitivity
for detecting foodborne pathogens, J. Agricult. Food Chem.,
63, 745-753.
65.Rodriguez, M. O., Covian, L. B., Garcia, A. C.,
and Blanco-Lopez, M. C. (2016) Silver and gold enhancement methods for
lateral flow immunoassays, Talanta, 148, 272-278.
66.Cao, X., Ye, Y., and Liu, S. (2011) Gold
nanoparticle-based signal amplification for biosensing, Anal.
Biochem., 417, 1-16.
67.Ryazantsev, D. Y., Voronina, D. V., and Zavriev,
S. K. (2016) Immuno-PCR: achievements and perspectives, Biochemistry
(Moscow), 81, 1754-1770.
68.Chang, L., Li, J., and Wang, L. (2016)
Immuno-PCR: an ultrasensitive immunoassay for biomolecular detection,
Anal. Chim. Acta, 910, 12-24.
69.Gooding, J. J., and Gaus, K. (2016)
Single-molecule sensors: challenges and opportunities for quantitative
analysis, Angewandte Chem. Int. Edn., 55,
11354-11366.
70.Ma, F., Li, Y., Tang, B., and Zhang, C. Y. (2016)
Fluorescent biosensors based on single-molecule counting, Accounts
Chem. Res., 49, 1722-1730.
71.Kuang, H., Xing, C., Hao, C., Liu, L., Wang, L.,
and Xu, C. (2013) Rapid and highly sensitive detection of lead ions in
drinking water based on a strip immunosensor, Sensors,
13, 4214-4224.
72.Stenberg, M., and Nygren, H. (1985) A diffusion
limited reaction theory for a solid-phase immunoassay, J. Theor.
Biol., 113, 589-597.
73.Stenberg, M., Werthen, M., Theander, S., and
Nygren, H. (1988) A diffusion limited reaction theory for a microtiter
plate assay, J. Immunol. Methods, 112, 23-29.
74.Stenberg, M., Stiblert, L., and Nygren, H. (1986)
External diffusion in solid-phase immunoassays, J. Theor. Biol.,
120, 129-140.
75.Klenin, K. V., Kusnezow, W., and Langowski, J.
(2005) Kinetics of protein binding in solid-phase immunoassays: theory,
J. Chem. Phys., 122, 214715.
76.Kusnezow, W., Syagailo, Y. V., Ruffer, S.,
Klenin, K., Sebald, W., Hoheisel, J. D., Gauer, C., and Goychuk, I.
(2006) Kinetics of antigen binding to antibody microspots: strong
limitation by mass transport to the surface, Proteomics,
6, 794-803.
77.Nadim, A. (2009) Modeling of mass transfer
limitation in biomolecular assays, Ann. N.Y. Acad. Sci.,
1161, 34-43.
78.Philibert, J. (2005) One and a half century of
diffusion: Fick, Einstein, before and beyond, Diffus.
Fundament., 2, 1-19.
79.Mehrer, H., and Stolwijk, N. A. (2009) Heroes and
highlights in the history of diffusion, Diffus. Fundament.,
11, 1-32.
80.Qian, S., and Bau, H. H. (2003) A mathematical
model of lateral flow bioreactions applied to sandwich assays, Anal.
Biochem., 322, 89-98.
81.Rath, D., and Panda, S. (2015) Contribution of
rotational diffusivity towards the transport of antigens in
heterogeneous immunosensors, Analyst, 140, 6579-6587.
82.Sadana, A., and Sadana, N. (2008) Fractal
Analysis of Binding and Dissociation of Protein–Analyte
Interactions on Biosensor Surfaces, Elsevier, Amsterdam, p.
361.
83.Kusnezow, W., Syagailo, Y. V., Ruffer, S.,
Baudenstiel, N., Gauer, C., Hoheisel, J. D., Wild, D., and Goychuk, I.
(2006) Optimal design of microarray immunoassays to compensate for
kinetic limitations theory and experiment, Mol. Cell.
Proteomics, 5, 1681-1696.
84.Zhao, M., Wang, X., and Nolte, D. (2010)
Mass-transport limitations in spot-based microarrays, Biomed. Optics
Express, 1, 983-997.
85.Dong, J., and Ueda, H. (2017) ELISA-type assays
of trace biomarkers using microfluidic methods, Nanomed.
Nanobiotechnol., 9, e1457.
86.Li, J., Zrazhevskiy, P., and Gao, X. (2016)
Eliminating size‐associated diffusion constraints for rapid
on‐surface bioassays with nanoparticle probes, Small,
12, 1035-1043.
87.Zhao, M. X., Li, J., and Gao, X. (2017)
Eliminating diffusion limitations at the solid-liquid interface for
rapid polymer deposition, ACS Biomater. Sci. Eng., 3,
782-786.
88.Wang, G., Driskell, J. D., Porter, M. D., and
Lipert, R. J. (2009) Control of antigen mass transport via capture
substrate rotation: binding kinetics and implications on immunoassay
speed and detection limits, Anal. Chem., 81,
6175-6185.
89.Wang, B., and Cheng, X. (2016) Enhancement of
binding kinetics on affinity substrates by laser point heating induced
transport, Analyst, 141, 1807-1813.
90.Driskell, J. D., Kwarta, K. M., Lipert, R. J.,
Vorwald, A., Neill, J. D., Ridpath, J. F., and Porter, M. D. (2006)
Control of antigen mass transfer via capture substrate rotation: an
absolute method for the determination of viral pathogen concentration
and reduction of heterogeneous immunoassay incubation times, J.
Virol. Methods, 138, 160-169.
91.Boraker, D. K., Bugbee, S. J., and Reed, B. A.
(1992) Acoustic probe-based ELISA, J. Immunol. Methods,
155, 91-94.
92.Chen, R., Weng, L., Sizto, N. C., Osorio, B.,
Hsu, C. J., Rodgers, R., and Litman, D. J. (1984)
Ultrasound-accelerated immunoassay, as exemplified by enzyme
immunoassay of choriogonadotropin, Clin. Chem., 30,
1446-1451.
93.Beumer, T., Haarbosch, P., and Carpay, W. (1996)
Convection during incubation of microplate solid phase immunoassay:
effects on assay response and variation, Anal. Chem., 68,
1375-1380.
94.Varfolomeev, S. D., and Gurevich, K. G. (1999)
Biokinetics: A Practical Course [in Russian], Fair-Press,
Moscow.
95.Qian, S., and Bau, H. H. (2004) Analysis of
lateral flow biodetectors: competitive format, Anal. Biochem.,
326, 211-224.
96.Ragavendar, M., and Anmol, C. M. (2012) A
mathematical model to predict the optimal test line location and sample
volume for lateral flow immunoassays, in Ann. Int. Conf. of the IEEE
Engineering in Medicine and Biology Society IEEE, pp.
2408-2411.
97.Landry, J. P., Ke, Y., Yu, G. L., and Zhu, X. D.
(2015) Measuring affinity constants of 1450 monoclonal antibodies to
peptide targets with a microarray-based label-free assay platform,
J. Immunol. Methods, 417, 86-96.
98.Atkins, P., and De Paula, J. (2006)
Physical Chemistry, W. H. Freeman and Company, N. Y., pp.
802-803.
99.Schlosshauer, M., and Baker, D. (2004) Realistic
protein–protein association rates from a simple diffusional model
neglecting long-range interactions, free energy barriers, and landscape
ruggedness, Protein Sci., 13, 1660-1669.
100.Maynard, J., and Georgiou, G. (2000) Antibody
engineering, Annu. Rev. Biomed. Eng., 2, 339-376.
101.Foote, J., and Eisen, H. N. (1995) Kinetic and
affinity limits on antibodies produced during immune responses,
Proc. Natl. Acad. Sci. USA, 92, 1254-1256.
102.Batista, F. D., and Neuberger, M. S. (1998)
Affinity dependence of the B cell response to antigen: a threshold, a
ceiling, and the importance of off-rate, Immunity, 8,
751-759.
103.Cauerhff, A., Goldbaum, F. A., and Braden, B.
C. (2004) Structural mechanism for affinity maturation of an
anti-lysozyme antibody, Proc. Natl. Acad. Sci. USA, 101,
3539-3544.
104.Chmura, A. J., Orton, M. S., and Meares, C. F.
(2001) Antibodies with infinite affinity, Proc. Natl. Acad. Sci.
USA, 98, 8480-8484.
105.Trisler, K., Looger, L. L., and Sharma, V.
(2007) A metalloantibody that irreversibly binds a protein antigen,
J. Biol. Chem., 282, 26344-26353.
106.Zheng, X., Bi, C., Li, Z., Podariu, M., and
Hage, D. S. (2015) Analytical methods for kinetic studies of biological
interactions: a review, J. Pharm. Biomed. Anal., 113,
163-180.
107.Sevlever, D., Bruera, M. R., and Gatti, C. A.
(1986) Measurement of antigen–antibody binding constants by
elution of affinity chromatography columns with continuous
concentration gradients of dissociating agents, Immunol.
Invest., 15, 497-503.
108.Heegaard, N. H. (1994) Determination of
antigen–antibody affinity by immuno-capillary electrophoresis,
J. Chromatogr. A, 680, 405-412.
109.Krylov, S. N. (2007) Kinetic CE: foundation for
homogeneous kinetic affinity methods, Electrophoresis,
28, 69-88.
110.Pan, Y., Sackmann, E. K., Wypisniak, K.,
Hornsby, M., Datwani, S. S., and Herr, A. E. (2016) Determination of
equilibrium dissociation constants for recombinant antibodies by
high-throughput affinity electrophoresis, Sci. Rep., 6,
39774.
111.Nikolovska-Coleska, Z., Wang, R., Fang, X.,
Pan, H., Tomita, Y., Li, P., Roller, P. P., Krajewski, K., Saito, N.
G., Stuckey, J. A., and Wang, S. (2004) Development and optimization of
a binding assay for the XIAP BIR3 domain using fluorescence
polarization, Anal. Biochem., 332, 261-273.
112.Xie, C., Dong, C., and Ren, J. (2009) Study on
homogeneous competitive immune reaction by fluorescence correlation
spectroscopy: using synthetic peptide as antigen, Talanta,
79, 971-974.
113.Gielen, F., Butz, M., Rees, E. J., Erdelyi, M.,
Moschetti, T., Hyvonen, M., Edel, J. B., Kaminski, C. F., and
Hollfelder, F. (2017) Quantitative affinity determination by
fluorescence anisotropy measurements of individual nanoliter droplets,
Anal. Chem., 89, 1092-1101.
114.Friguet, B., Chaffotte, A. F.,
Djavadi-Ohaniance, L., and Goldberg, M. E. (1985) Measurements of the
true affinity constant in solution of antigen–antibody complexes
by enzyme-linked immunosorbent assay, J. Immunol. Methods,
77, 305-319.
115.Hardy, F., Djavadi-Ohaniance, L., and Goldberg,
M. E. (1997) Measurement of antibody/antigen association rate constants
in solution by a method based on the enzyme-linked immunosorbent assay,
J. Immunol. Methods, 200, 155-159.
116.Goldberg, M. E., and Djavadi-Ohaniance, L.
(1993) Methods for measurement of antibody/antigen affinity based on
ELISA and RIA, Curr. Opin. Biotechnol., 5, 278-281.
117.Stevens, F. J., and Bobrovnik, S. A. (2007)
Deconvolution of antibody affinities and concentrations by non-linear
regression analysis of competitive ELISA data, J. Immunol.
Methods, 328, 53-58.
118.Bobrovnik, S. A., Demchenko, M., Komisarenko,
S., and Stevens, F. (2010) Traditional ELISA methods for antibody
affinity determination fail to reveal the presence of low affinity
antibodies in antisera: an alternative approach, J. Mol.
Recognit., 23, 448-456.
119.Bobrovnik, S. (2005) New capabilities in
determining the binding parameters for ligand–receptor
interaction, J. Biochem. Biophys. Methods, 65, 30-44.
120.Bobrovnik, S. A. (2003) Determination of
antibody affinity by ELISA. Theory, J. Biochem. Biophys.
Methods, 57, 213-236.
121.Bobrovnik, S. A. (2002) Ligand–receptor
interaction. Klotz–Hunston problem for two classes of binding
sites and its solution, J. Biochem. Biophys. Methods, 52,
135-143.
122.Rich, R. L., and Myszka, D. G. (2008) Survey of
the year 2007 commercial optical biosensor literature, J. Mol.
Recognit., 21, 355-400.
123.Schasfoort, R. B. M., and Tudos, A. J. (2008)
Handbook of Surface Plasmon Resonance, Royal Society of
Chemistry, Cambridge, p. 403.
124.Schuck, P. (1997) Reliable determination of
binding affinity and kinetics using surface plasmon resonance
biosensors, Curr. Opin. Biotechnol., 8, 498-502.
125.Mehand, M. S., Crescenzo, G. D., and
Srinivasan, B. (2014) On‐line kinetic model discrimination for
optimized surface plasmon resonance experiments, J. Mol.
Recognit., 27, 276-284.
126.Edwards, D. A. (2004) Refining the measurement
of rate constants in the BIAcore, J. Math. Biol., 49,
272-292.
127.Mason, T., Pineda, A. R., Wofsy, C., and
Goldstein, B. (1999) Effective rate models for the analysis of
transport-dependent biosensor data, Math. Biosci., 159,
123-144.
128.O’Shannessy, D. J. (1994) Determination
of kinetic rate and equilibrium binding constants for macromolecular
interactions: a critique of the surface plasmon resonance literature,
Curr. Opin. Biotechnol., 5, 65-71.
129.Kolosova, A. Y., Samsonova, J. V., and Egorov,
A. M. (2000) Competitive ELISA of chloramphenicol: influence of
immunoreagent structure and application of the method for the
inspection of food of animal origin, Food Agricult. Immunol.,
12, 115-125.
130.Zvereva, E. A., Byzova, N. A., Sveshnikov, P.
G., Zherdev, A. V., and Dzantiev, B. B. (2015) Cut-off on demand:
adjustment of the threshold level of an immunochromatographic assay for
chloramphenicol, Anal. Methods, 7, 6378-6384.
131.Dzantiev, B. B., Zherdev, A. V., Romanenko, O.
G., and Sapegova, L. A. (1996) Development and comparative study of
different immunoenzyme techniques for pesticides detection, Int. J.
Environ. Anal. Chem., 65, 95-111.
132.Macken, C. A., and Perelson, A. S. (1982)
Aggregation of cell surface receptors by multivalent ligands, J.
Math. Biol., 14, 365-370.
133.Yang, T., Baryshnikova, O. K., Mao, H., Holden,
M. A., and Cremer, P. S. (2003) Investigations of bivalent antibody
binding on fluid-supported phospholipid membranes: the effect of hapten
density, J. Am. Chem. Soc., 125, 4779-4784.
134.Hlavacek, W. S., Posner, R. G., and Perelson,
A. S. (1999) Steric effects on multivalent ligand–receptor
binding: exclusion of ligand sites by bound cell surface receptors,
Biophys. J., 76, 3031-3043.
135.Reynolds, J. A. (1979) Interaction of divalent
antibody with cell surface antigens, Biochemistry, 18,
264-269.
136.Gelinsky-Wersing, D., Wersing, W., and Pompe,
W. (2017) Bivalent kinetic binding model to surface plasmon resonance
studies of antigen–antibody displacement reactions, Anal.
Biochem., 518, 110-125.
137.Winzor, D. J. (2011) Allowance for antibody
bivalence in the characterization of interactions by ELISA, J. Mol.
Recognit., 24, 139-148.
138.Vos, Q., Klasen, E. A., and Haaijman, J. J.
(1987) The effect of divalent and univalent binding on antibody
titration curves in solid-phase ELISA, J. Immunol. Methods,
103, 47-54.
139.Perelson, A. S., DeLisi, C., and Weigel, F. W.
(1984) Some mathematical models of receptor clustering by multivalent
ligands, in Cell Surface Dynamics, Marcell Dekker, New York, pp.
223-277.
140.Larsson, A. (1989) Divalent binding of
monoclonal antibody to a cell surface antigen. Modelling of equilibrium
data, Mol. Immunol., 26, 735-739.
141.Shiau, L. D. (1995) Modeling the average
molecular weights of antigen–antibody complexes by probability
theory, J. Immunol. Methods, 178, 267-275.
142.Joshi, R. R. (1995) Statistical mechanics of
antibody–antigen binding: affinity analysis, Phys. A
Statistic. Mech. Appl., 218, 214-228.
143.Van Opheusden, J. H. J., Wiegel, F. W., and
Goldstein, B. (1984) Forward rate constants for receptor clusters
variational methods for upper and lower bounds, Biophys. Chem.,
20, 237-248.
144.Hlavacek, W. S., Perelson, A. S., Sulzer, B.,
Bold, J., Paar, J., Gorman, W., and Posner, R. G. (1999) Quantifying
aggregation of IgE-FceRI by multivalent antigen, Biophys. J.,
76, 2421-2431.
145.Hendrickson, O. D., Zherdev, A. V., Kaplun, A.
P., and Dzantiev, B. B. (2002) Experimental study and mathematical
modeling of the interaction between antibodies and antigens on the
surface of liposomes, Mol. Immunol., 39, 413-422.
146.Dmitriev, D. A., Massino, Y. S., Segal, O. L.,
Smirnova, M. B., Pavlova, E. V., Kolyaskin, G. I., Gurevich, K. G.,
Gnedenko, O. V., Ivanov, Y. D., Archakov, A. I., Osipov, A. P.,
Dmitriev, A. D., and Egorov, A. M. (2002) Analysis of bispecific
monoclonal antibody binding to immobilized antigens using an optical
biosensor, Biochemistry (Moscow), 67, 1356-1365.
147.Edeling, M. A., Austin, S. K., Shrestha, B.,
Dowd, K. A., Mukherjee, S., Nelson, C. A., Johnson, S., Mabila, M. N.,
Christian, E. A., Rucker, J., and Pierson, T. C. (2014) Potent dengue
virus neutralization by a therapeutic antibody with low monovalent
affinity requires bivalent engagement, PLoS Pathog., 10,
e1004072.
148.Crothers, D., and Metzger, H. (1972) The
influence of polyvalency on the binding properties of antibodies,
Immunochemistry, 9, 341-357.
149.Berson, S. A., and Yalow, R. S. (1959)
Quantitative aspects of reaction between insulin and insulin-binding
antibody, J. Clin. Invest., 38, 1996-2016.
150.Taylor, J., Picelli, G., and Harrison, D. J.
(2001) An evaluation of the detection limits possible for competitive
capillary electrophoretic immunoassays, Electrophoresis,
22, 3699-3708.
151.Wang, Z. X. (1995) An exact mathematical
expression for describing competitive binding of two different ligands
to a protein molecule, FEBS Lett., 360, 111-114.
152.Roehrl, M. H., Wang, J. Y., and Wagner, G.
(2004) A general framework for development and data analysis of
competitive high-throughput screens for small-molecule inhibitors of
protein–protein interactions by fluorescence polarization,
Biochemistry, 43, 16056-16066.
153.Rodbard, D., Ruder, H. J., Vaitukaitis, J., and
Jacobs, H. S. (1971) Mathematical analysis of kinetics of radioligand
assays: improved sensitivity obtained by delayed addition of labeled
ligand, J. Clin. Endocrinol. Metab., 33, 343-355.
154.Dzantiev, B. B., and Yuriev, D. K. (1988) Some
regularities of immunochemical analysis. A sequential saturation
method, Appl. Biochem. Microbiol., 24, 830-838.
155.Rodbard, D., and Feldman, Y. (1978) Kinetics of
two-site immunoradiometric (“sandwich”) assays. I:
Mathematical models for simulation, optimization, and curve fitting,
Immunochemistry, 15, 71-76.
156.Miles, L. E. M., Bieber, C. P., Eng, L. F., and
Lipschtz, D. A. (1974) Properties of two-site immunoradiometric
(labelled antibody) assay systems, in Radioimmunoassay and Related
Procedures in Medicine, Proceedings of the International Atomic Energy
Agency, 149, 163.
157.Rey, E. G., O’Dell, D., Mehta, S., and
Erickson, D. (2017) Mitigating the hook effect in lateral flow sandwich
immunoassays using real-time reaction kinetics, Anal. Chem.,
89, 5095-5100.
158.Jassam, N., Jones, C. M., Briscoe, T., and
Horner, J. H. (2006) The hook effect: a need for constant vigilance,
Ann. Clin. Biochem., 43, 314-317.
159.Rodbard, D., Feldman, Y., Jaffe, M. L., and
Miles, L. E. M. (1978) Kinetics of two-site immunoradiometric
(“sandwich”) assays. II: Studies on the nature of
the-high-dose hook effect, Immunochemistry, 15,
77-82.
160.Ryall, R. G., Story, C. J., and Turner, D. R.
(1982) Reappraisal of the causes of the “hook effect” in
two-site immunoradiometric assays, Anal. Biochem., 127,
308-315.
161.Fernando, S. A., and Wilson, G. S. (1992)
Studies of the “hook” effect in the one-step sandwich
immunoassay, J. Immunol. Methods, 151, 47-66.
162.Zherdev, A. V., and Dzantiev, B. B. (1996)
Formation of antibody–antigen–antibody complexes on the
solid phase: experimental study and mathematical modeling, Appl.
Biochem. Microbiol., 32, 194-202.
163.Morris, B. A., and Sadana, A. (2005) A fractal
analysis of pathogen detection by biosensors, Biophys. Chem.,
113, 67-81.
164.Butala, H. D., Tan, Y., and Sadana, A. (2004)
Analyte–receptor binding on surface plasmon resonance biosensors:
a fractal analysis of Cre–loxP interactions and the influence of
Cl, O, and S on drug–liposome interactions, Anal.
Biochem., 332, 10-22.
165.Butala, H. D., and Sadana, A. (2004) Binding
and dissociation kinetics using fractals: an analysis of electrostatic
effects and randomly coupled and oriented coupled receptors on
biosensor surfaces, Biosens. Bioelectron., 19,
933-944.
166.Muller, R. (1998) A mathematical model to
predict the effects of temperature on timed ELISA, Food Agricult.
Immunol., 10, 297-305.
167.Sittampalam, G. S., Smith, W. C., Miyakawa, T.
W., Smith, D. R., and McMorris, C. (1996) Application of experimental
design techniques to optimize a competitive ELISA, J. Immunol.
Methods, 190, 151-161.
168.Tsoi, J., Patel, V., and Shih, J. (2014) A
practical approach to automate randomized design of experiments for
ligand-binding assays, Bioanalysis, 6, 705-713.
169.Ohmura, N., Tsukidate, Y., Shinozaki, H.,
Lackie, S. J., and Saiki, H. (2003) Combinational use of antibody
affinities in an immunoassay for extension of dynamic range and
detection of multiple analytes, Anal. Chem., 75,
104-110.
170.Model, M. A., and Healy, K. E. (1999)
Optimization of the cost and sensitivity of receptor- and enzyme-based
assays, Anal. Biochem., 271, 59-69.
171.Wild, D. (2013) The Immunoassay Handbook:
Theory and Applications of Ligand Binding, ELISA and Related
Techniques, Elsevier Ltd., Kidlington.
172.Van Emon, J. M. (2007) Immunoassay and Other
Bioanalytical Techniques, CRC Press, Taylor Francis, Boca
Raton.
173.Schuurman, H. J., and De Ligny, C. L. (1979)
Physical models of radioimmunoassay applied to the calculation of the
detection limit, Anal. Chem., 51, 2-7.
174.Hemmila, I., Dakubu, S., Mukkala, V.-M.,
Siitari, H., and Lovgren, T. (1984) Europium as a label in
time-resolved immunofluorometric assays, Anal. Biochem.,
137, 335-343.
175.Griswold, W. (1987) Theoretical analysis of the
sensitivity of the solid phase antibody assay (ELISA), Mol.
Immunol., 24, 1291-1294.
176.Jackson, T. M., and Ekins, R. P. (1986)
Theoretical limitations on immunoassay sensitivity: current practice
and potential advantages of fluorescent Eu3+ chelates as
non-radioisotopic tracers, J. Immunol. Methods, 87,
13-20.
177.Rissin, D. M., Kan, C. W., Campbell, T. G.,
Howes, S. C., Fournier, D. R., Song, L., Piech, T., Patel, P. P.,
Chang, L., Rivnak, A. J., Ferrell, E. P., Randall, J. D., Provuncher,
G. K., Walt, D. R., and Duffy, D. C. (2010) Single-molecule
enzyme-linked immunosorbent assay detects serum proteins at
subfemtomolar concentrations, Nat. Biotechnol., 28,
595-599.
178.Tessler, L. A., and Mitra, R. D. (2011)
Sensitive single‐molecule protein quantification and protein
complex detection in a microarray format, Proteomics, 11,
4731-4735.
179.Schmidt, R., Jacak, J., Schirwitz, C., Stadler,
V., Michel, G., Marme, N., Schutz, G. J., Hoheisel, J. D., and
Knemeyer, J.-P. (2011) Single-molecule detection on a protein-array
assay platform for the exposure of a tuberculosis antigen, J.
Proteome Res., 10, 1316-1322.
180.Brown, E. N., McDermott, T. J., Bloch, K. J.,
and McCollom, A. D. (1996) Defining the smallest analyte concentration
an immunoassay can measure, Clin. Chem., 42, 893-903.
181.O’Connor, T., and Gosling, J. P. (1997)
The dependence of radioimmunoassay detection limits on antibody
affinity, J. Immunol. Methods, 208, 181-189.
182.Ekins, R., and Kelso, D. (2011) Single-molecule
ELISA, Clin. Chem., 57, 372-375.
183.Yakovleva, J., Zherdev, A. V., Popova, V. A.,
Eremin, S. A., and Dzantiev, B. B. (2003) Production of antibodies and
development of enzyme-linked immunosorbent assays for the herbicide
butachlor, Anal. Chim. Acta, 491, 1-13.
184.Ferreira, S. L. C., Dos Santos, W. N. L.,
Quintella, C. M., Neto, B. B., and Bosque-Sendra, J. M. (2004) Doehlert
matrix: a chemometric tool for analytical chemistry (review),
Talanta, 63, 1061-1067.
185.Ferreira, S. L. C., Bruns, R. E., Ferreira, H.
S., Matos, G. D., David, J. M., Brandao, G. C., Da Silva. E. G. P.,
Portugal, L. A., Dos Reis, P. S., Souza, A. S., and Dos Santos, W. N.
L. (2007) Box–Behnken design: an alternative for the optimization
of analytical methods, Anal. Chim. Acta, 597,
179-186.
186.Jeney, C., Dobay, O., Lengyel, A., Adam, E.,
and Nasz, I. (1999) Taguchi optimization of ELISA procedures, J.
Immunol. Methods, 223, 137-146.
187.Luo, W., Pla-Roca, M., and Juncker, D. (2011)
Taguchi design-based optimization of sandwich immunoassay microarrays
for detecting breast cancer biomarkers, Anal. Chem., 83,
5767-5774.
188.Avella-Oliver, M., Gimenez-Romero, D., Morais,
S., Gonzalez-Martinez, M. A., Bueno, P. R., Puchades, R., and
Maquieira, A. (2013) INSEL: an in silico method for optimizing
and exploring biorecognition assays, Chem. Commun., 49,
10868-10870.
189.Joelsson, D., Moravec, P., Troutman, M.,
Pigeon, J., and DePhillips, P. (2008) Optimizing ELISAs for precision
and robustness using laboratory automation and statistical design of
experiments, J. Immunol. Methods, 337, 35-41.
190.Rodbard, D., and Lewald, J. E. (1970) Computer
analysis of radioligand assay and radioimmunoassay data, Acta
Endocrinol. Suppl. (Copenhagen), 147, 79-103.
191.Ezan, E., Tiberghien, C., and Dray, F. (1991)
Practical methods for optimizing radioimmunoassay detection and
precision limit, Clin. Chem., 37, 226-230.
192.Choi, D. H., Katakura, Y., Matsuda, R.,
Hayashi, Y., Ninomiya, K., and Shioya, S. (2007) Simulation model for
predicting limit of detection and range of quantitation of competitive
enzyme-linked immunosorbent assay, J. Biosci. Bioeng.,
103, 427-431.
193.Karpinski, K. F. (1990) Optimality assessment
in the enzyme-linked immunosorbent assay (ELISA), Biometrics,
46, 381-390.
194.Hayashi, Y., Matsuda, R., Maitani, T., Imai,
K., Nishimura, W., Ito, K., and Maeda, M. (2004) Precision, limit of
detection and range of quantitation in competitive ELISA, Anal.
Chem., 76, 1295-1301.
195.He, X., Coombs, D., Myszka, D. G., and
Goldstein, B. (2006) A theoretical and experimental study of
competition between solution and surface receptors for ligand in a
Biacore flow cell, Bull. Math. Biol., 68, 1125-1150.
196.Barak-Shinar, D., Rosenfeld, M., Zisman, E.,
and Abboud, S. (2000) A computational fluid dynamic model of
antigen–antibody surface adsorption on a piezoelectric
immunosensor, Ann. Biomed. Eng., 28, 565-571.
197.Barak-Shinar, D., Rosenfeld, M., and Abboud, S.
(2004) Numerical simulations of mass-transfer processes in 3D model of
electrochemical sensor, J. Electrochem. Soc., 151,
H261-H266.
198.Sarraguca, J. M. G., Lopes, J. A., Santos, J.
L., and Lima, J. L. (2012) Mathematical simulation of signal profiles
in flow analysis, Anal. Lett., 45, 85-98.
199.Kolev, S. D. (1995) Mathematical modelling of
flow-injection systems, Anal. Chim. Acta, 308, 36-66.
200.Hage, D. S., Thomas, D. H., Chowdhuri, A. R.,
and Clarke, W. (1999) Development of a theoretical model for
chromatographic-based competitive binding immunoassays with
simultaneous injection of sample and label, Anal. Chem.,
71, 2965-2975.
201.Ahmad, A. L., Low, S. C., Shukor, S. R. A.,
Fernando, W. J. N., and Ismail, A. (2010) Hindered diffusion in lateral
flow nitrocellulose membrane: experimental and modeling studies, J.
Membr. Sci., 357, 178-184.
202.Zeng, N., Wang, Z., Li, Y., Du, M., and Liu, X.
(2011) Inference of nonlinear state-space models for sandwich-type
lateral flow immunoassay using extended Kalman filtering, IEEE
Transact. Biomed. Eng., 58, 1959-1966.
203.Fu, E., Nelson, K. E., Ramsey, S. A., Foley, J.
O., Helton, K., and Yager, P. (2009) Modeling of a competitive
microfluidic heterogeneous immunoassay: sensitivity of the assay
response to varying system parameters, Anal. Chem., 81,
3407-3413.
204.Zeng, N., Wang, Z., Zhang, H., and Alsaadi, F.
E. (2016) A novel switching delayed PSO algorithm for estimating
unknown parameters of lateral flow immunoassay, Cognit. Comput.,
8, 143-152.
205.Krishnamoorthy, S., Makhijani, V. B., Lei, M.,
Giridharan, M. G., and Tisone, T. (2000) Computational studies of
membrane-based test formats, in Technical Proc. 2000 Int. Conf. on
Modeling and Simulation of Microsystems, pp. 590-593.
206.Liu, Z., Hu, J., Li, A., Feng, S., Qu, Z., and
Xu, F. (2017) The effect of report particle properties on lateral flow
assays: a mathematical model, Sens. Actuat. B Chem., 248,
699-707.