REVIEW: High-Pressure Scanning Microcalorimetry – A New Method for Studying Conformational and Phase Transitions
S. A. Potekhin
Institute of Protein Research, Russian Academy of Sciences, 142290 Pushchino, Moscow Region, Russia; E-mail: spot@vega.protres.ru
Received June 24, 2017; Revision received July 13, 2017
The development of high-pressure scanning microcalorimetry and the first results studying transitions in proteins, lipids, and model polymers are reviewed. Special attention is given to changes (increments) in volume parameters upon transitions as well as the nature of these changes. It is demonstrated that the use of the model of compound transfer reaction in its purest form for assessment of denaturation volume effects failed due to serious difficulties.
KEY WORDS: scanning microcalorimetry, high pressure, theoretical analysis, macromoleculesDOI: 10.1134/S0006297918140110
Developing novel research methods is a basis for emerging technologies for obtaining new knowledge. Information breakthrough in any area of science is usually preceded by the development of a new technique or approach providing the possibility of obtaining information that was not available previously, or its acquisition was extremely difficult.
From the thermodynamic point of view, the interest in the effect of high pressure on molecules is no less than the effect of temperature. Nevertheless, thousands (if not tens of thousands) of articles are published annually with the results of investigation of the effect of temperature on various materials, while the number of publications on the effect of pressure is by at least an order of magnitude less. This fact reflects the lack of highly sensitive commercially available equipment for such studies. Rapid growth in the number of publications investigating the effect of high pressure conducted using in-house-made instrumentation reflects increasing interest in the possibilities that this area of science can offer. The results of such studies can be very useful both for investigation of fundamental issues of molecular biology and biophysics, as well as being applied for solving various problems of biotechnology [1-5].
First, it is known that the investigation of the effect of pressure on conformational transitions of macromolecules reveals denaturation and activation volumes, which is rather difficult to do under constant pressure. Measurements of these parameters for various objects allow accumulation of certain statistics on the correlation between the structure of a macromolecule and changes of its partial volume as a result of transition. This, in turn, could be a basis for developing a semiempirical theory relating the structural parameters of a macromolecule with denaturation and/or activation volumes.
Second, the possibilities for biotechnological applications of high pressure are very broad. In particular, high pressure can be used for industrial enzyme production (medicinal drugs and industrial enzymes). It is a well-known fact that the main problem in production of recombinant proteins by expressing any gene in bacteria often involves renaturation of the produced proteins, which are frequently accumulated in inactive form in inclusion bodies [6]. On the other hand, kinetic investigations of renaturation show that the main problem in the selection of renaturation conditions is aggregation of intermediate partially folded protein forms [7-11]. High pressure noticeably suppresses aggregation [12, 13], which suggests that significantly higher yields of an active product could be formed during renaturation under high pressure.
Third, the application of high pressure in food industry is also of interest [14, 15]. This is because proteins can denature under high pressure even at room temperature. On the other hand, protein denaturation is a key issue in most food technology processes. Denaturation of proteins in food materials results in formation of product structures that define their appeal to consumers. In addition, protein denaturation in pathogenic organisms present in the raw material offers sterilization, and hence safety and extended shelf life of the food product [16]. Protein denaturation in traditional food technology occurs by heating to high temperatures (above 100°C). Denaturation during the heating is accompanied by several undesirable processes of decay or modification of many food components, such as vitamins, aroma forming compounds, amino acids, lipids, and carbohydrates. Hence, the possibility of reducing denaturation temperature by increasing pressure seems especially attractive. This method can, for example, be used for manufacturing food products with extended shelf life and composition corresponding to physiological requirements of humans to a high degree.
Elucidation of the principles of self-organization and maintenance of structure of macromolecules in living organisms inhabiting large depths at very high pressure (up to 1000 atm) is another fundamental question. The same issue is important for proteins in hyperthermophiles [17, 18]; in contrast to most proteins from other sources, they can be stabilized by high pressure.
Regarding the abovementioned, the detailed and systematic investigation of thermodynamic stability of macromolecules under high pressure as well as of the nature of volume changes upon conformational transitions is necessary for the wide implementation of high pressure in scientific studies, biotechnology, and food technology. The significant growth in the number of publications devoted to investigation of the effect of high pressure on very different biologically significant macromolecules and living organisms indicates growing interest in these problems.
The change in volume resulting from various processes is a very important thermodynamic parameter defining the effect of increasing pressure. However, scientific knowledge on the nature of volume changes occurring upon conformational transformations of macromolecules is insufficient. On the other hand, knowledge of the dependence of enthalpy of any conformational transition on temperature and pressure could enable calculating volume changes upon transition as well as increments of isobaric thermal expansion and isothermal compressibility.
In 2007-2009, the Institute of Protein Research of the Russian Academy of Sciences developed and manufactured, in collaboration with the Vereshchagin Institute of High Pressure Physics of the Russian Academy of Sciences, a unique scanning microcalorimeter capable of operating at pressures up to 6000 atm [19, 20]. Testing showed that this instrument had no analogs. Not more than 0.3 mg of biological material (proteins, nucleic acids, lipids, etc.) is required to make reliable measurements. Similar instruments known from international publications can work at the pressure of 200 atm at best and demonstrate an order of magnitude lower sensitivity. The Russian instrument provides information on the dependence of enthalpy of conformational transitions of biologically important macromolecules (proteins, polynucleic acids, lipids, polysaccharides) on temperature and pressure, which in turn provides the beginning of systematic investigations of volume changes upon conformational transitions of biologically important macromolecules. The goal of this review is to demonstrate the potential of high-pressure scanning microcalorimetry and to present results obtained in recent years.
PHOSPHOLIPIDS
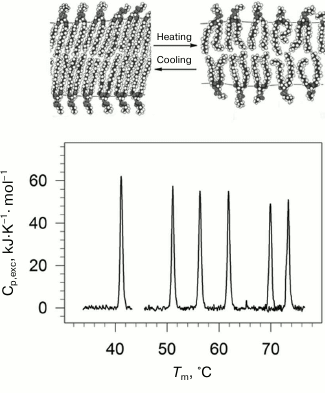
Lipids are an important structural class of biological molecules. Lipids are amphiphilic compounds; their molecules are comprised of a polar headgroup and one or several possible hydrophobic “tails”. Phospholipids are esters of polyhydric alcohols and long-chain fatty acids. They contain a residue of phosphoric acid with an attached additional group of different chemical nature. Lipids in water can form a bilayer structure – the main element of cell membranes. In a bilayer, lipid molecules are stacked as two parallel monolayers facing each other by their hydrophobic surfaces. The lipid bilayer can undergo a phase transition with rising of temperature (Fig. 1). The low temperature state (gel-like state) is an analog of the solid state. The high temperature state (liquid-crystal state) is more like the liquid state but has a certain degree of order [21, 22].
Fig. 1. Temperature-dependences of excess partial molar heat capacity of DPPC (1,2-diacylpalmitoylphosphatidylcholine) dispersion in water at different pressures (bottom part). From left to right: 0.0981, 53.4, 84.1, 116.6, 164.3, 186.7 MPa. In the upper part of the figure, schematic representation of phase transition in lipid bilayer membrane from the low-temperature gel phase (on the left) to the high temperature liquid crystal phase (on the right).
Physiological temperatures as a rule correspond to the lipid membranes’ phase transition region, which enables a high level of fluctuational mobility of the membranes. The level of fluctuation is determined among other things by the expansion and compression factors. On the other hand, mechanical properties of membranes, which determine such biologically important processes as fusion of cells and bending of the membrane, are also determined by volume parameters [23-25]. Hence, it is important to know the features of changes in energy and volume parameters of lipid membranes upon the gel to liquid-crystal transition.
Using high pressure calorimetry, we investigated in detail the behavior of the main conformational transition (gel to liquid-crystal) for a group of homologous phospholipids – 1,2-diacylphosphatidylcholines with different length of hydrophobic “tails” [26-29]. The melting curves for DPPC (16:0 PC, 1,2-dipalmitoyl-sn-glycero-3-phosphocholine) under different pressures are presented as an example in Fig. 1. It was found that the transition temperature increased nonlinearly with increasing length of the “tail”. Increasing pressure to 200 MPa (~2000 atm) increased the lipid melting temperature by approximately 34°C.
We developed a mathematics allowing to analyze the experimental calorimetric data and to interpret the results [30, 31]. We were able to estimate the changes of the main partial thermodynamic functions upon the transition including increments of volume, as well as increments of isothermal compressibility and isobaric thermal expansion. The dependence of thermodynamic functions’ increments on pressure and acyl chain length was analyzed.
We found that the lipid bilayer increased its partial volume upon the transition by no more than a few percent (3.2% for DPPC) under ambient pressure. It is interesting to note that the melting heat of lipids of this class per methylene group (CH2) of the hydrophobic “tail” is close to the value for melting of alkanes and polyethylene. Hence, from the energy point of view, the cost of acquiring a certain degree of mobility of CH2 groups in polymer materials and in hydrophobic “tails” of phosphatidylcholines is almost the same. The availability of water to both sides of the lipid bilayer has practically no effect on the “energy cost” of the methylene group movement.
We found that the melting heat (enthalpy) of homologous lipids with the same polar “head” but different hydrophobic acyl chain length was proportional to the length (number of carbon atoms N) of this chain at any pressure [22, 27, 28, 32-34]. The same is true for the volume change on the transition:
where NΔH=0 and NΔV=0 are the number of carbon atoms in one acyl chain at which enthalpy and volume increments turn to zero; ΔhCH2 and ΔvCH2 are the incremental (per methylene group) transition enthalpy and volume, respectively. Such behavior is related to the fact that the increase in sufficiently long lipid “tails” by one methylene group does not change the number of groups in the boundary region of the hydrophobic monolayer. Only the number of practically equivalent methylene groups fully immersed in the hydrophobic layer changes. It is obvious that such linear dependences will be maintained under any conditions (pH, ionic strength, pressure, temperature).
An important conclusion follows from the equations of classic thermodynamics. If the enthalpy of transition becomes zero at a certain acyl chain length NΔH=0, then the volume increment of the same lipid under the same conditions must be zero as well. This follows from the Clausius–Clapeyron relation, for example:
Here Tm is the absolute temperature of transition, and P is the pressure.
Hence, in Eqs. (1) and (2), NΔH=0 = NΔV=0, and
In other words, the change in enthalpy and the change in volume of the transition must be zero for the same acyl chain length. Two non-trivial conclusions can be drawn from these results.
(i) The ratio of the volume change to the enthalpy change for homologous lipids with different acyl chain length is a constant value depending only on pressure, but not on N:
Relation (5) can be obtained by simple division of Eq. (4) by Eq. (2).
The constancy of the ratio of volume change to enthalpy change was first established empirically [23, 24] by comparing the data of scanning microcalorimetry and densitometry under ambient pressure, but later it was confirmed and explained in our studies [27-29] using the high-pressure microcalorimetry technique.
(ii) The second nontrivial consequence based on above-mentioned reasons looks as follows. Plots of the logarithm of the transition temperatures versus pressure are always parallel for transitions in homologous lipids.
In other words, the pressure derivatives of the logarithm of transition temperature are identical for all homologous lipids under any conditions.
This follows from the Clausius–Clapeyron relation (Eq. (3)) and relation (5). Indeed:
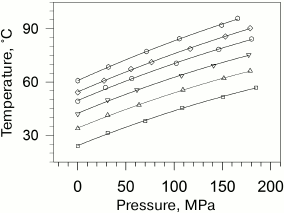
Taking into account that the absolute values of transition temperatures change insignificantly, it becomes clear that the plots of temperatures versus pressure will be also close by their slopes. The dependences of the gel to liquid crystal transition temperatures for phosphatidylcholines are presented in Fig. 2 [27].
Fig. 2. Dependences of melting temperatures of multilamellar vesicles of 1,2-diacylphosphatidylcholines in water on pressure (data from [27]). Solid lines represent the best approximations of the experimental dependences. The dependences correspond to (from top to bottom) lipids with acyl chain lengths from 14 carbon atoms (14:0 PC) to 19 carbon atoms (19:0 PC). The following symbol designations are used: 14:0 PC (open squares), 15:0 PC (open triangles), 16:0 PC (inverted open triangles), 17:0 PC (open circles), 18:0 PC (open rhombi), and 19:0 PC (open hexagons).
It should be noted that though the nature of the polar “head” of a lipid molecule can affect the stability of transitions, it does not result in violation of the above regularity because the melting of all lipids is analogous to that of alkanes. This means that for lipids with another “head” but with the same acyl chains, the both consequences will be also valid. Moreover, the ratio of enthalpy to volume change for any lipids with two saturated acyl chains but with other polar heads will be similar.
We established an interesting trend during theoretical analysis of the effect of pressure on a single-step transition [31]. We found that depending on the relation both of the apparent expansion coefficient of transition αm = (1/ΔV)(∂ΔV/∂Tp) and the inverse transition temperature, the enthalpy (heat) of transition can either decrease or increase. At αm > Tm-1 the enthalpy will decrease with pressure growth (∂ΔHm/∂P < 0), while at αm < Tm-1 it will increase (∂ΔHm/∂P > 0). At αm = Tm-1 the enthalpy will be independent of pressure (∂ΔHm/∂P = 0). Here ΔHm and Tm are enthalpy and temperature of melting, respectively.
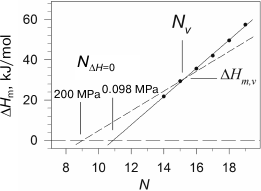
We observed such behavior of the melting enthalpy with increasing pressure during investigation of diacylphosphatidylcholines with hydrophobic “tails” of different length [28]. The transition enthalpy increases in the case of short lipids, while it decreases in the case of long ones, which is related to the fact that the coefficient αm changes correspondingly. Considering that the dependence of ΔHm on N is linear, it is clear that there is such a length Nv for a virtual lipid for which the transition enthalpy would not depend on pressure. We have shown that such lipid in the case of phosphatidylcholines will have the length Nv ≈ 15.5 and enthalpy ΔHm,v ≈ 31 kJ/mol. It follows from the above that the graphical displays of the linear function of the enthalpy increment versus N with growing pressure will merely rotate around the point with coordinates Nv and ΔHm,v, which corresponds to this virtual lipid (Fig. 3). It can also be seen from the figure that the intercept point of the dependence of enthalpy on N with abscissa axis, NΔH=0(P), shifts towards the area of shorter lipids with increasing pressure. For example, NΔH=0 ≈ 10.9 under ambient pressure, and this point shifts to NΔH=0 ≈ 9.1 under 200 MPa. The availability of the intercept point indicates that the gel phase is energy-wise disadvantageous for short lipids (N < 12), and such lipids will be in liquid-crystal form at any temperature, if they are able to form a bilayer structure at all. The gel state, however, can probably be observed in lipids with N of 10 and 11 carbon atoms under pressure of 2000 atm and above.
Fig. 3. Dependences of melting enthalpy of 1,2-diacylphosphatidylcholines in water on the length of acyl chain N (adapted from [28]). The solid line represents the best linear approximation of the experimental dependence obtained under ambient pressure. The dashed line corresponds to 200 MPa pressure (calculated based on experimental data).
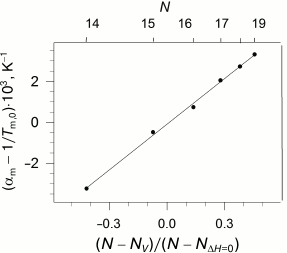
The availability of the indicated specific correlation between the length of the lipid hydrophobic “tail”, its enthalpy of melting, and pressure imposes certain limitations on the dependence of the coefficients of thermal expansion and isothermal compression on the length of the lipid “tail”. As we reported earlier [28], these coefficients demonstrate nonlinear dependence on N, but the function becomes linear if the parameter (N - Nv)/(N - NΔH=0) is used as an argument (Fig. 4).
Fig. 4. Dependency of the difference between the apparent coefficient of isobaric expansibility of transition and inverse temperature of transition at ambient pressure versus parameter (N − Nv)/(N − NΔH=0) (see text), which is appropriate to the different acyl chain length N (top abscissa axis). Data adapted from [28]. The solid line represents the best linear approximation of the dependence.
COIL–GLOBULE TRANSITION IN MODEL POLYMERS VERSUS
TEMPERATURE
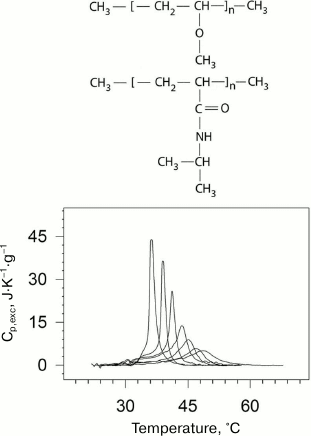
The “smart” stimulus-responsive polymers that are capable of self-organization in aqueous medium are very promising for application in various biomedical fields – from targeted drug delivery to gene expression and modeling of behavior of proteins and enzymes [35, 36]. Elucidation of the principles and mechanisms of self-organization of such polymers in aqueous solutions as well as theoretical description of their behavior is of fundamental importance for polymer science. In the case of amphiphilic polymers, self-organization is governed by the balance of hydrophobic and hydrophilic elements in their structure. External factors can shift this balance, causing inter- and intramolecular association of chemical groups in the polymer and formation of ordered structure (globules, micelles, networks, and others). Temperature is one of the most important parameters of the environment. Some thermosensitive polymers can undergo cooperative reversible transitions of the “coil–globule” type in aqueous environments, the physical nature and mechanism of which are essentially related to the transitions in proteins [37-39]. Poly(N-isopropylacrylamide) (PNIPAM) [40] and poly(vinylmethyl ether) (PVME) [41] are examples of such polymers (Fig. 5).
Fig. 5. Dependences of excess partial heat capacity of PNIPAM on temperature (bottom) at pressures (from left to right): 0.0981 (ambient pressure); 38.2; 52.3; 91.1; 127; 156; 201 MPa. Structural formulas of PVME and PNIPAM (top to bottom) are presented in the upper part of the figure.
PNIPAM is a chemical isomer of polyleucine with a polar peptide group not in the main, but in the side chain. PNIPAM undergoes the coil–globule transition in aqueous solution upon heating, which can be considered as an intramolecular transition from the unfolded state to the molten globule state [42]. A similar transition but likely a more complex one is observed for PVME [43]. The physical nature and mechanism of these transitions is to some extent similar to the transitions related to protein renaturation [37-39]. Like in the case of proteins, this process is accompanied by significant negative increment of heat capacity. The latter indicates significant dehydration of the hydrophobic surface in both cases. The dependences of the transition temperature and enthalpy on pressure from 1 to 2000 atm were obtained in the experiments.
In the case of PNIPAM, an increase in pressure results in a decrease in enthalpy and increase in the half-width of the transition, while the transition temperature in this range of pressures demonstrates dependence with a maximum [44] (Fig. 5). Hence, the change in partial volume upon the transition is positive at low pressures and negative at high pressures.
In the case of PVME, the thermograms of phase separation were more complicated [45]. Two special points have been observed during melting: the point (Tt,1, binodal) and the point of three phases coexistence (Tt,2). The temperature Tt,1 drops by 10°C, and the temperature Tt,2 increases by 15°C with increasing pressure, while the transition enthalpy decreases 1.5-fold and the increment of heat capacity remains practically unchanged. These data indicate that the sequential phase transitions that occur in dilute aqueous solution of poly(vinylmethyl ether) upon heating are of different nature.
PROTEINS
Elaboration of a comprehensive and adequate model of globular protein stabilization that also takes into account volume effects is one of the important and required steps in protein physics [46]. This area of science has been developing intensively in recent decades. In particular, the applicability of the two-state model for the description of denaturation of single-domain globular proteins has been demonstrated experimentally [47, 48]. The contribution of different interactions to enthalpy and energy of protein structure stabilization was estimated [49]. It was established that hydrophobic interactions provide a significant contribution to structure stabilization [50-52].
It is known that unfolding (denaturation) of globular proteins is accompanied by a large change in its heat capacity [47, 53]. It is also known that similar large changes in heat capacity occur upon hydration of nonpolar compounds [54-56]. These facts as well as the dehydration of the nonpolar surface of a protein molecule during self-assembly of its 3D structure allowed suggesting that the hydration of nonpolar groups during denaturation was the main reason for the large increment of the heat capacity upon denaturation of proteins. A quantitative correlation between the area of the nonpolar surface of a protein that was hydrated additionally because of unfolding and the denaturation increment of heat capacity was demonstrated [57]. The contribution of hydration of the polar surface to the heat capacity increment usually does not exceed 20% [55, 56]. Thus, the heat capacity increment can be considered as a measure of the hydrophobic surface area hydrated as a result of unfolding. The algorithm developed by Privalov and Makhatadze estimates some thermodynamic functions of protein structure stabilization based on its structure and data on transfer of model compounds from nonpolar solvent to water [49, 55, 58]. Hence, it seemed that the model compound transfer reactions are adequate for estimating thermodynamic functions of protein structure stabilization and for explaining the high increment of heat capacity value.
Unfortunately, our understanding of the reasons for the volume change during protein denaturation was not so detailed. Usually, the scale of denaturation volume increment does not exceed 1% of the total volume of a protein molecular and, in most cases, has a value of several dozens of milliliters per mol [59, 60]. Despite the small value, the denaturation increment of the volume is an important thermodynamic parameter defining how an increase of pressure affects the stability of protein structure.
Factors that could contribute to the change in protein volume during denaturation are more or less known [60, 61]. The first and most obvious reason for volume change during denaturation is the availability of cavities not filled with solvent in its native structure. Another significant contribution could be due to the well-known phenomenon of the change in liquid volume under the action of molecular electric fields – so-called electrostriction [59, 62]. In particular, the availability of abnormally titrated groups in proteins that change their charge during denaturation is well recognized, which in turn could cause the change in thermodynamic volume of the molecule [63, 64]. Investigation of hydration of model compounds showed that the change in protein molecule volume during denaturation due to hydration of the additional surface of the polypeptide chain could also be significant [65]. It is also clear that other types of interactions exist, such as hydrogen bonds that could lead to change in volume [61, 66].
It is important to note that all the cited contributions are of approximately the same order of magnitude per protein group as the denaturation volume increment of entire protein molecules. Hence, it follows from the very general consideration that the value of the denaturation volume increment (the change in volume because of denaturation) is determined as a compromise between the multitudes of contributions of different nature, which are similar in value to the resulting volume. This complicates the task of accurate theoretical estimation of the denaturation volume increment.
Attempts to use data on transfer of model compounds from a liquid hydrophobic environment into water for estimation of the denaturation volume increments immediately met significant obstacles. For example, Kauzmann [67] mentioned that “the model of transfer of liquid hydrocarbons almost failed in attempts to use it for explaining the effect of pressure on protein folding”.
Similar conclusions were made by some other authors [62, 68]. The following considerations served as a basis for this. A small nonpolar molecule decreases its thermodynamic volume by 10-20 ml/mol upon the transfer from a liquid hydrocarbon environment into water under ambient pressure. Increase in pressure results in growth of this change to a small positive value (approximately 5 ml/mol) [69, 70]. Hence, if the protein hydrophobic core is similar to liquid hydrocarbons and if a significant number of nonpolar groups (say 10 or 20) are exposed to water upon protein denaturation, then under ambient pressure, the absolute value of ΔV must be large and negative (from –100 to –400 ml/mol), and under high pressure – smaller and positive (from 50 to 100 ml/mol). As a rule, proteins do not behave as described above. Under low pressure, ΔV has small positive or negative values, while ΔV can decrease with increasing pressure and have negative values up to tens of milliliters per mole of protein [5, 62, 69, 71]. This phenomenon is known in the literature as the “protein volume paradox” [72].
In this regard, another issue has attracted our attention. Under low pressure the mentioned phenomena can make only negative contributions to the total denaturation volume increment, and it is not clear what makes this volume small or even slightly positive. In contrast to the negative contributions, the origin of positive contributions to the denaturation volume increment remains controversial. In this case, we do not consider the positive contribution to the volume increment due to protonation of abnormally titrated groups. This phenomenon does exist [63, 64], but it can affect the denaturation volume increment only in a narrow pH range where the degree of dissociation of groups in the native and denatured state differs significantly.
The hypothesis of a dominating contribution of inner cavities in protein structure to the total denaturation volume increment is also internally controversial. The authors of some studies practically deny the contribution of additional hydration and electrostriction into volume increment, which contradicts the data on model compounds. They suggest that “pressure unfolds proteins mainly due to cavities that are present in the folded state and absent in the unfolded one” [73, 74].
Considering these contradictions in the understanding of the nature of the positive increment of the denaturation volume, several authors suggested a more accurate in their view model in which denaturation at high pressure is modeled not by the process of hydration of nonpolar compounds, but by the process of transfer of water molecules to the nonpolar medium – hydrophobic protein core [62, 72, 75]. It is known that the change in volume for the process of water transfer to dichloroethane is +2 ml/mol, the transfer of water to benzene or trichloroethane results in the volume change of +4 ml/mol, and in the case of water transfer to carbon tetrachloride the change in volume can reach +14 ml/mol [76]. This model was first suggested to explain the effect of high pressure on the rate of denaturation of globular proteins [77]. It was shown that the activation enthalpy becomes negative at high pressure. It was assumed in this model that an increase in pressure results in penetration of individual water molecules into the hydrophobic protein core, accompanied by the significant release of heat. The hypothesis was suggested for modeling of an activated state, but later it was extended to the equilibrium denatured state.
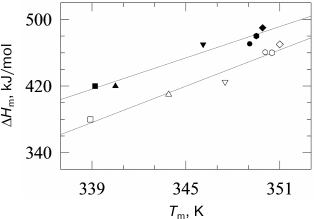
To test this hypothesis, we investigated the effect of high pressure on denaturation of lysozyme and RNase [78]. The main experimental result of this work was verification of absence of a significant effect of high pressure on the denaturation increment of heat capacity Δcp of globular proteins at pressure up to 2000 atm (Fig. 6). As mentioned previously, the denaturation increment of heat capacity is the direct consequence of the hydrophobic effect. The change in the heat capacity increment under high pressure could be explained by two factors – diminishing of this effect due to change in water structure near hydrophobic surface under the action of pressure and/or by change in the amount of additionally hydrated surface of the protein molecule during denaturation. The absence of significant changes in Δcp indicates lack of significant effect of pressure on these processes.
Fig. 6. Dependences of lysozyme denaturation enthalpy versus temperature of denaturation at ambient pressure (filled symbols) and at 178 MPa (open symbols). Experimental points were obtained at the following pH: 2.50 (open squares), 2.75 (open triangles), 3.00 (inverted open triangles), 4.00 (open circles), 4.50 (open rhombi), and 5.00 (open hexagons). Straight lines are drawn by the least-squares method for every pressure.
The absence of a noticeable effect of high pressure on the heat capacity increment was corroborated by the results [71] showing that the use of this suggestion leads to a noncontradictory phase diagram for chymotrypsin at pressures up to 7000 atm. The diagram is well compatible with the experimentally observed temperature of cold denaturation at high pressure. It should be noted that cold denaturation is basically impossible if the denaturation heat capacity increment vanishes. This follows from the fact that at zero Δcp, the Gibbs energy is a linear function of temperature and cannot cross the temperature axis at two different temperatures. The fact of cold denaturation phenomenon at high pressure itself corroborates the retention of high values of heat capacity increment at this condition [79-82].
The next important conclusion is the absence of principle changes in the character of hydration and the area of hydrophobic surface additionally hydrated upon denaturation. We interpret the character of hydration here through the hydration properties of water penetrating into the hydrophobic core of protein molecule. Does water penetrate in the form of individual molecules or small groups of molecules losing some of its macroscopic properties (such as surface tension or ability for hydrating separate nonpolar groups according to certain laws), or does it maintain its properties as a liquid? Our data argue that upon denaturation of globular proteins there is no such situation, when under low pressure hydration of hydrophobic groups corresponds to the transfer of nonpolar compounds to water, and while at elevated pressure unfolding must be modeled by the transfer of individual water molecules into the nonpolar environment. A change in the character of hydration would unavoidably lead to a significant decrease in the heat capacity increment and, probably in a change in denaturation cooperativity. Nothing of the kind has been observed. The argumentation [72], that at high pressure the denatured protein contains a remarkable amount of secondary structure and its hydrodynamic sizes are significantly smaller than in denaturant solutions at ambient pressure, does not prove anything. Some heat- or cold-denatured proteins at ambient pressure behave similarly (they have a high content of secondary structure and relatively small size) [83], but their heat capacity increment is well compatible with the model compound transfer reactions. So, it seems very likely that at high pressure the volumes of water penetrating inside the denatured protein are sufficient to be considered as indivisible macroscopic object.
Hence, the conclusion that the processes of denaturation and the degrees of hydration of nonpolar groups under ambient and high pressures (up to 2000 atm) are very similar is a fundamental result. Models suggesting significant changes in the character of hydration of globular proteins in the denatured state under high pressure can hardly be considered appropriate. This is corroborated by direct measurements of the hydration shell of the krypton atom in water using the X-ray absorption spectroscopy technique [84]. The authors of that work state that “contrary to what had been previously thought the direct hydrophobic hydration shell is highly resistant to any perturbation by pressure”.
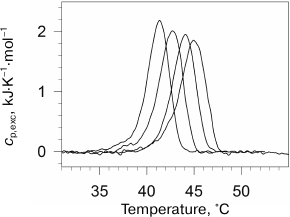
We also investigated the effect of high pressure on the denaturation transition of the collagen protein [85]. As known, collagen has a specific helical structure. Collagen forms 2-3 intramolecular hydrogen bonds per three amino acid residues and does not have a hydrophobic core [86]. The excess heat capacity of collagen under several pressures is presented in Fig. 7. As seen in the figure, pressure stabilizes collagen structure, but it does not affect cooperativity of its denaturation transition. Pressure significantly decreases the denaturation enthalpy. In contrast to denaturation of most globular proteins, denaturation of collagen at ambient pressure occurs with an increase in the partial volume. Moreover, the absolute change in collagen volume is significantly larger than for most proteins. The change in volume decreases with increasing pressure due to the difference in the compressibility of the protein in the folded and unfolded states. This effect is compensated to some degree by the differences in the coefficients of thermal expansion.
Fig. 7. Excessive molar (per amino acid residue) partial heat capacity of collagen in water at different pressures. Pressure was (from left to right): 0.0981, 41.3, 108, 180 MPa.
As to elucidation of the nature of positive contribution to the denaturation volume increment of proteins, it must be mentioned that collagen is a very convenient model for discussing this issue. The lack of a hydrophobic core and, therefore, the relatively small hydrophobic surface area hydrated during denaturation represents an essential difference of this protein from globular proteins. It was found [85] that the denaturation volume increment of collagen under normal pressure was +1.1·10–2 cm3/g, which is significantly larger than the value observed for globular proteins (~–10–3 cm3/g). Taking into account that denaturation of collagen involves only rupture of intramolecular hydrogen bonds and increase in polypeptide chain mobility, and that water achieves additional access predominately to the polar surface, it is clear that precisely these events can produce the larger volume increase. Hence, the large positive contribution to the denaturation volume increment of any protein at normal pressure is capable of releasing the polypeptide chain itself followed by its hydration. It is clear that the intramolecular hydrogen bonds cause a decrease in the physical volume of molecules in the native conformation and, hence, must also provide positive contribution to the denaturation volume increment in the absence of hydration of the released groups. However, in the case of the rupture of intramolecular hydrogen bonds followed by the formation of hydrogen bonds with water molecules, the resulting contribution to the volume increment can be of either sign.
COMPARISON OF RESULTS OBTAINED WITH MATERIALS OF DIFFERENT
NATURE
Despite the difference in chemical structure of the investigated objects, a comparison of the experimental results allows better understanding of the nature of the protein denaturation volume increment. As known, denaturation of globular proteins is accompanied by additional hydration of hydrophobic groups previously shielded from water. The significant increase in partial heat capacity (heat capacity increment) of the protein is due to this particular phenomenon. Moreover, a significant increase in mobility of all groups including hydrophobic ones located in the protein core is observed during denaturation. Some time ago, the notion of “dry molten globule” was introduced for analysis of the causes of denaturation cooperativity [87]. It was assumed that under certain conditions a native protein could undergo a cooperative transition resulting in a significant increase in mobility of structural elements due to a slight decrease in the packing density of the molecule (increase in the globule size). It was also suggested that the accessibility of the protein hydrophobic groups to water was practically unchanged by such transition. The transition of a protein molecule from the native state to the dry molten globule state can be considered as an analog of melting of solids. The protein molecule converts from the “quasi-crystal” to “quasi-liquid” state. With this terminology, protein denaturation in general can be considered as a two-step process: (a) transition from a densely packed state with low mobility of side groups to the dry molten globule state, and (b) transition from the dry molten globule state to the unfolded well-hydrated state.
As to the “protein volume paradox”, it can be stated that the investigated objects are sufficiently good models with the help of which the reasons for the contradictions established previously can be significantly clarified. In particular, the gel–liquid crystal transition in lipids represents a transition from a state, where hydrophobic groups are dehydrated and their mobility is restricted to a significant degree, to a state with dehydrated but mobile hydrophobic groups. The initial state can model a native protein state to a certain degree, and the final state is similar to the “dry molten globule” in terms of the above terminology (transition a). The heat capacity increment is practically absent due to the lack of additional hydration of the hydrophobic surface (see the table). The transition is accompanied by large heat absorption (220 J/g) and by relatively large increase in the partial volume (16·10–2 cm3/g). The transition is also characterized by a relatively large ratio of the volume change to the enthalpy change (7.1·10–4 cm3/J), which implies significant dependence of the temperature of this transition on pressure. The latter statement follows from the Clausius–Clapeyron relation (6).
Thermodynamic parameters of thermotropic transitions in macromolecules
of different chemical nature under ambient pressure
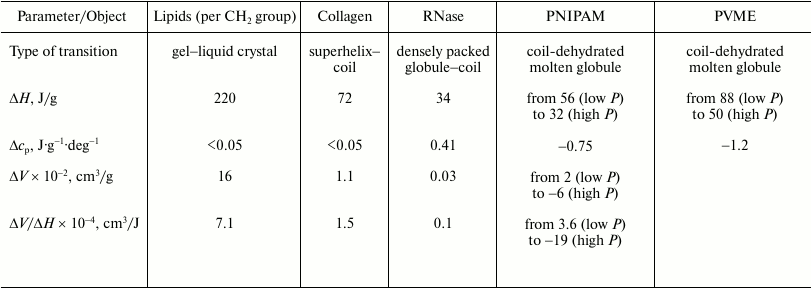
Note: ΔH and ΔV are partial changes
(increments) in enthalpy and volume upon transition;
Δcp is the partial change (increment) of heat
capacity. PNIPAM, poly(N-isopropylacrylamide); PVME, poly(vinylmethyl
ether). Data on lipids are for phosphatidylcholines.
The transition of the high-temperature form of PNIPAM (globule) to the low-temperature form (coil) is a transition from the state where the hydrophobic groups are mobile but essentially dehydrated (the state similar to the dry molten globule) to the state with hydrated mobile hydrophobic groups (case b). The final state in this sense is similar to the state of a denatured protein. Due to the large additional hydration of the hydrophobic surface, this transition is accompanied (see table) by a large heat capacity increment (~1 J·g–1·deg–1), by noticeable heat release (–56 J/g), and by a detectible volume decrease (–2·10–2 cm3/g).
Hence, it follows from the above two results that the transition (a) in the protein from the native state to the state of dry molten globule should be accompanied by a large absorption of heat and by a large volume increase. The following transition (b) from the state of dry molten globule to the unfolded hydrated state compensates significantly for the denaturation enthalpy and can decrease the denaturation volume increment by an order of magnitude. It is interesting to note that a small nonpolar molecule decreases its volume by 10-20 ml/mol during transfer from liquid hydrocarbon medium to water under ambient pressure, which could compensate for the increase in volume during the “dry” melting of the protein globule associated with the protein side group of 4-8 methylenes.
Hence, the main reason for the manifestation of the apparent “protein volume paradox” is the suggestion that hydration of nonpolar groups of the hydrophobic core during protein denaturation can be modeled by their transfer from liquid hydrocarbon medium to water. However, this process models only the second step of denaturation (step b). Judging from the results of the lipid gel–liquid crystal transition, the packing density of hydrocarbon chains below the melting temperature is much larger than the density of liquid hydrocarbons. It seems plausible that the transfer of hydrophobic groups from a solid nonpolar environment to water would be a better model.
We conclude from the results of the studies that high-pressure scanning microcalorimetry can provide unique information on volume changes during conformational transitions of macromolecules. This promises to facilitate development of the physical understanding of macromolecules and creation of novel and adequate models for stabilization of their structure taking into account, among other factors, volume effects.
REFERENCES
1.Mozhaev, V. V., Heremans, K., Frank, J., Masson,
P., and Balny, C. (1996) High pressure effects on protein structure and
function, Proteins, 24, 81-91.
2.Panick, G., Malessa, R., Winter, R., Rapp, G.,
Frye, K. J., and Royer, C. A. (1998) Structural characterization of the
pressure-denatured state and unfolding/refolding kinetics of
staphylococcal nuclease by synchrotron small-angle X-ray scattering and
Fourier-transform infrared spectroscopy, J. Mol. Biol.,
275, 389-402.
3.Robinson, C. R., and Sigar, S. G. (1995)
Hydrostatic and osmotic pressure as tools to study macromolecular
recognition, Methods Enzymol., 259, 395-427.
4.Takeda, N., Kato, M., and Taniguchi, Y. (1995)
Pressure- and thermally-induced reversible changes in the secondary
structure of ribonuclease: studies by FT-IR spectroscopy,
Biochemistry, 34, 5980-5987.
5.Yamaguchi, T., Yamada, H., and Akasaka, K. (1995)
Thermodynamics of unfolding of ribonuclease a under high pressure. A
study by proton NMR, J. Mol. Biol., 250, 689-694.
6.Clark, E. D. B. (1998) Refolding of recombinant
proteins, Curr. Opin. Biotechnol., 9, 157-163.
7.Chrunyk, B. A., Evans, J., Lillquist, J., Young,
P., and Wetzel, R. (1993) Inclusion body formation and protein
stability in sequence variants of interleukin-1 beta, J. Biol.
Chem., 268, 18053-18061.
8.King, J., Haase-Pettingell, C., Robinson, A. S.,
Speed, M., and Mitraki, A. (1996) Thermolabile folding intermediates:
inclusion body precursors and chaperonin substrates, FASEB J.,
10, 57-66.
9.Mitraki, A., Fane, B., Haase-Pettingell, C.,
Sturtevant, J., and King, J. (1991) Global suppression of protein
folding defects and inclusion body formation, Science,
253, 54-58.
10.Panda, M., Gorovits, B. M., and Horowitz, P. M.
(2000) Productive and nonproductive intermediates in the folding of
denatured rhodanese, J. Biol. Chem., 275, 63-70.
11.Speed, M. A., Wang, D. I., and King, J.
(1996) Specific aggregation of partially folded polypeptide
chains: the molecular basis of inclusion body composition, Nat.
Biotechnol., 14, 1283-1287.
12.Gorovits, B. M., and Horowitz, P. M. (1998) High
hydrostatic pressure can reverse aggregation of protein folding
intermediates and facilitate acquisition of native structure,
Biochemistry, 37, 6132-6135.
13.St. John, R. J., Carpenter, J. F., and Randolph,
T. W. (1999) High pressure fosters protein refolding from aggregates at
high concentrations, Proc. Natl. Acad. Sci. USA, 96,
13029-13033.
14.Denys, S., Ludikhuyze, L. R., Van Loey, A. M.,
and Hendrickx, M. E. (2000) Modeling conductive heat transfer and
process uniformity during batch high-pressure processing of foods,
Biotechnol. Prog., 16, 92-101.
15.Buckow, R., Sikes, A., and Tume, R. (2013) Effect
of high pressure on physicochemical properties of meat, Crit. Rev. Food
Sci. Nutr., 53, 770-786.
16.Tauscher, B. (1995) Pasteurization of food by
hydrostatic high pressure: chemical aspects, Z. Lebensm Unters.
Forsch., 200, 3-13.
17.Summit, M., Scott, B., Nielson, K., Mathur, E.,
and Baross, J. (1998) Pressure enhances thermal stability of DNA
polymerase from three thermophilic organisms, Extremophiles,
2, 339-345.
18.Sun, M. M., Tolliday, N., Vetriani, C., Robb, F.
T., and Clark, D. S. (1999) Pressure-induced thermostabilization of
glutamate dehydrogenase from the hyperthermophile Pyrococcus
furiosus, Protein Sci., 8, 1056-1063.
19.Senin, A. A., Dzhavadov, L. N., and Potekhin, S.
A. (2016) High-pressure differential scanning microcalorimeter, Rev.
Sci. Instrum., 87, 034901.
20.Potekhin, S. A., Senin, A. A., Abdurakhmanov, N.
N., and Mezhburd, E. V., RF Patent 2364845, Differential Adiabatic
High Pressure Scanning Microcalorimeter, March 19, 2008 (registered
August 20, 2009).
21.Melchior, D. L., and Steim, J. M. (1976)
Thermotropic transitions in biomembranes, Annu. Rev. Biophys.
Bioeng., 5, 205-238.
22.Marsh, D. (1991) General features of phospholipid
phase transitions, Chem. Phys. Lipids, 57, 109-120.
23.Heimburg, T. (1998) Mechanical aspects of
membrane thermodynamics. Estimation of the mechanical properties of
lipid membranes close to the chain melting transition from calorimetry,
Biochim. Biophys. Acta, 1415, 147-162.
24.Ebel, H., Grabitz, P., and Heimburg, T. (2001)
Enthalpy and volume changes in lipid membranes. I. The proportionality
of heat and volume changes in the lipid melting transition and its
implication for the elastic constants, J. Phys. Chem. B,
105, 7353-7360.
25.Grabitz, P., Ivanova, V. P., and Heimburg, T.
(2002) Relaxation kinetics of lipid membranes and its relation to the
heat capacity, Biophys. J., 82, 299-309.
26.Potekhin, S. A., Senin, A. A., Abdurakhmanov, N.
N., and Khusainova, R. S. (2008) High pressure effect on the main
transition from the ripple gel P'β phase to the
liquid crystal (Lα) phase in
dipalmitoylphosphatidylcholine. Microcalorimetric study, Biochim.
Biophys. Acta, 1778, 2588-2593.
27.Potekhin, S. A., Senin, A. A., Abdurakhmanov, N.
N., and Khusainova, R. S. (2011) Thermodynamic invariants of gel to the
liquid crystal 1,2-diacylphosphatidylcholines transition, Biochim.
Biophys. Acta, 1808, 1806-1810.
28.Potekhin, S. A., Senin, A. A., and Khusainova, R.
S. (2013) Thermodynamics of the gel to liquid crystal
1,2-diacylphosphatidylcholines transition. High-pressure
microcalorimetry, Thermochim. Acta, 560, 17-26.
29.Potekhin, S. A., and Khusainova, R. S. (2017)
Acyl chain length dependencies of energy and volume dependent
parameters upon the gel to liquid crystal transition of
1,2-diacylphosphatidylcholines. Theoretical consideration, Biophys.
Chem., 227, 29-33.
30.Potekhin, S. A. (2012) The potential of scanning
microcalorimetry for studying thermotropic conformational transitions
in biomacromolecules, Polymer Sci. Ser. C, 54,
108-115.
31.Potekhin, S. A., Yegorov, A. E., and Khusainova,
R. S. (2015) A thermodynamic analysis of two-state transitions under
high pressure. Theoretical considerations, Biophysics,
60, 687-691.
32.Mason, J. T., and Huang, C.-H. (1981) Chain
length dependent thermodynamics of saturated symmetric-chain
phosphatidylcholine bilayers, Lipids, 16, 604-608.
33.Nagle, J. F., and Wilkinson, D. A. (1978)
Lecithin bilayers. Density measurement and molecular interactions,
Biophys. J., 23, 159-175.
34.Mabrey, S., and Sturtevant, J. M. (1976)
Investigation of phase transitions of lipids and lipid mixtures by high
sensitivity differential scanning calorimetry, Proc. Natl. Acad.
Sci. USA, 73, 3862-3866.
35.Gil, E. S., and Hudson. S. A. (2004)
Stimuli-responsive polymers and their bioconjugates, Prog. Polym.
Sci., 29, 1173-1222.
36.Alarcon, C. D. H., Pennadam, S., and Alexander,
C. (2005) Stimuli responsive polymers for biomedical applications,
Chem. Soc. Rev., 34, 276-285.
37.Graziano, G. (2000) On the temperature-induced
coil to globule transition of poly-N-isopropylacrylamide in
dilute aqueous solutions, Int. J. Biol. Macromol., 27,
89-97.
38.Bruscolini, P., Buzano, C., Pelizzola, A., and
Pretti, M. (2002) Lattice model for polymer hydration: collapse of
poly(N-isopropylacrylamide), Macromol. Symp., 181, 261-273.
39.Burova, T. V., Grinberg, N. V., Grinberg, V. Y.,
Tang, Y. T., Zhang, G. Z., and Khokhlov, A. R. (2008)
Order–disorder conformational transitions of
N-isopropylacrylamide-sodium styrene sulfonate copolymers in aqueous
solutions, Macromolecules, 41, 5981-5984.
40.Schild, H. G. (1992)
Poly(N-isopropylacrylamide): experiment, theory and application,
Prog. Polym. Sci., 17, 163-249.
41.Loozen, E., Nies, E., Heremans, K., and
Berghmans, H. (2006) The influence of pressure on the lower critical
solution temperature miscibility behavior of aqueous solutions of
poly(vinyl methyl ether) and the relation to the compositional
curvature of the volume of mixing, J. Phys. Chem. B, 110,
7793-7802.
42.Wu, C., and Zhou, S. (1996) First observation of
the molten globule state of a single homopolymer chain, Phys. Rev.
Lett., 77, 3053.
43.Schafer-Soenen, H., Moerkerke, R., Berghmans, H.,
Koningsveld, R., Dusek, K., and Solc, K. (1997) Zero and off-zero
critical concentrations in systems containing polydisperse polymers
with very high molar masses. 2. The system water–poly(vinyl
methyl ether), Macromolecules, 30, 410-416.
44.Grinberg, V. Y., Senin, A. A., Grinberg, N. V.,
Burova, T. V., Dubovik, A. S., Potekhin, S. A., and Erukhimovich, I.
Ya. (2015) High pressure effects under phase separation of aqueous
solutions of poly(N-isopropylacrylamide): a HS-DSC study,
Polymer, 64, 14-18.
45.Grinberg, V. Y., Burova, T. V., Grinberg, N. V.,
Dubovik, A. S., Senin, A. A., Potekhin, S. A., and Erukhimovich, I. Ya.
(2016) Energetics of phase separation in aqueous solutions of
poly(vinyl methyl ether), Polymer, 87, 283-289.
46.Finkelstein, A. V., and Ptitsyn, O. B. (2002) in
Protein Physics: A Course of Lectures, Academic Press, New
York.
47.Privalov, P. L., and Khechinashvili, N. N. (1974)
A thermodynamic approach to the problem of stabilization of globular
protein structure: a calorimetric study, J. Mol. Biol.,
86, 665-684.
48.Liu, Y., and Sturtevant, J. M. (1996) The
observed change in heat capacity accompanying the thermal unfolding of
proteins depends on the composition of the solution and on the method
employed to change the temperature of unfolding, Biochemistry,
35, 3059-3062.
49.Makhatadze, G. I., and Privalov, P. L. (1995)
Energetics of protein structure, Adv. Protein Chem., 47,
307-425.
50.Privalov, P. L., and Gill, S. J. (1988) Stability
of protein structure and hydrophobic interaction, Adv. Protein
Chem., 39, 191-234.
51.Makhatadze, G. I., and Privalov, P. L. (1993)
Contribution of hydration to protein folding thermodynamics: I. The
enthalpy of hydration, J. Mol. Biol., 232, 639-659.
52.Privalov, P. L., and Makhatadze, G. I. (1993)
Contribution of hydration to protein folding thermodynamics: II. The
entropy and Gibbs energy of hydration, J. Mol. Biol.,
232, 660-679.
53.Privalov, P. L. (1979) Stability of proteins:
small globular proteins, Adv. Protein Chem., 33,
167-241.
54.Baldwin, R. L. (2013) Properties of hydrophobic
free energy found by gas–liquid transfer, Proc. Natl. Acad.
Sci. USA, 110, 1670-1673.
55.Spolar, R. S., Livingstone, J. R., and Record, M.
T. (1992) Use of liquid hydrocarbon and amide transfer data to estimate
contributions to thermodynamic functions of protein folding from the
removal of nonpolar and polar surface from water, Biochemistry,
31, 3947-3955.
56.Myers, J. K., Pace, C. N., and Scholtz, J. M.
(1995) Denaturant m values and heat capacity changes: relation to
changes in accessible surface areas of protein unfolding, Protein
Sci., 4, 2138-2148.
57.Privalov, P. L., and Makhatadze, G. I. (1992)
Contribution of hydration and non-covalent interactions to the heat
capacity effect on protein unfolding, J. Mol. Biol., 224,
715-723.
58.Privalov, P. L., and Makhatadze, G. I. (1990)
Heat capacity of proteins: II. Partial molar heat capacity of the
unfolded polypeptide chain of proteins: protein unfolding effects,
J. Mol. Biol., 213, 385-391.
59.Mozhaev, V. V., Heremans, K., Frank, J., Masson,
P., and Balny, C. (1996) High pressure effects on protein structure and
function, Proteins, 24, 81-91.
60.Royer, C. A. (2002) Revisiting volume changes in
pressure-induced protein unfolding, Biochim. Biophys. Acta,
1595, 201-209.
61.Boonyaratanakornkit, B. B., Park, C. B., and
Clark, D. S. (2002) Pressure effects on intra- and intermolecular
interactions within proteins, Biochim. Biophys. Acta,
1595, 235-249.
62.Brandts, J. F., Oliveira, R. J., and Westort, C.
(1970) Thermodynamics of protein denaturation. Effect of pressure on
the denaturation of ribonuclease A, Biochemistry, 9,
1038-1047.
63.Rasper, J., and Kauzmann, W. (1962) Volume
changes in protein reactions. I. Ionization reactions of proteins,
J. Am. Chem. Soc., 84, 1771-1777.
64.Kauzmann, W., Bodanszky, A., and Rasper, J.
(1962) Volume changes in protein reactions. II. Comparison of
ionization reactions in proteins and small molecules, J. Am. Chem.
Soc., 84, 1777-1788.
65.Gross, M., and Jaenicke, R. (1994) Proteins under
pressure. The influence of high hydrostatic pressure on structure,
function and assembly of proteins and protein complexes, Eur. J.
Biochem., 221, 617-630.
66.Van Eldik, R., Asano, T., and Le Noble, W. J.
(1989) Activation and reaction volumes in solution, Chem. Rev.,
89, 549-688.
67.Kauzmann, W. (1987) Thermodynamics of unfolding,
Nature, 325, 763-764.
68.Dill, K. A. (1990) Dominant forces in protein
folding, Biochemistry, 29, 7133-7155.
69.Zipp, A., and Kauzmann, W. (1973) Pressure
denaturation of metmyoglobin, Biochemistry, 12,
4217-4228.
70.Sawamura, S., Nagaoka, K., and Machikawa, T.
(2001) Effects of pressure and temperature on the solubility of
alkylbenzenes in water:top
volumetric property of hydrophobic hydration, J. Phys. Chem.
B, 105, 2429-2436.
71.Hawley, S. A. (1971) Reversible
pressure-temperature denaturation of chymotrypsinogen,
Biochemistry, 10, 2436-2442.
72.Meersman, F., Dobson, C. M., and Heremans, K.
(2006) Protein unfolding, amyloid fibril formation and configurational
energy landscapes under high pressure conditions, Chem. Soc.
Rev., 35, 908-917.
73.Roche, J., Caro, J. A., Norberto, D. R., Barthe,
P., Roumestand, C., Schlessman, J. L., Garcia, A. E.,
García-Moreno, B. E., and Royer, C. A. (2012) Cavities determine
the pressure unfolding of proteins, Proc. Natl. Acad. Sci. USA,
109, 6945-6950.
74.Rouget, J. B., Aksel, T., Roche, J., Saldana, J.
L., Garcia, A. E., Barrick, D., and Royer, C. A. (2011) Size and
sequence and the volume change of unfolding, J. Am. Chem. Soc.,
133, 6020-6027.
75.Meersman, F., Daniel, I., Bartlett, D. H.,
Winter, R., Hazael, R., and McMillan, P. F. (2013) High-pressure
biochemistry and biophysics, Rev. Mineral Geochem., 75,
607-648.
76.Masterton, W. L., and Seiler, H. K. (1968)
Apparent and partial molal volumes of water in organic solvents, J.
Phys. Chem., 72, 4257-4262.
77.Suzuki, K. (1960) Studies on the kinetics of
protein denaturation under high pressure, Rev. Phys. Chem. Jap.,
29, 91-98.
78.Yegorov, A. Y., and Potekhin, S. A. (2015)
Moderate pressure has no distinct impact on hydrophobic hydration of
proteins, Thermochim. Acta, 610, 10-15.
79.Kunugi, S., and Tanaka, N. (2002) Cold
denaturation of proteins under high pressure, Biochim. Biophys.
Acta, 1595, 329-344.
80.Zhang, J., Peng, X., Jonas, A., and Jonas, J.
(1995) NMR study of the cold, heat, and pressure unfolding of
ribonuclease A, Biochemistry, 34, 8631-8641.
81.Nash, D. P., and Jonas, J. (1997) Structure of
pressure-assisted cold denatured lysozyme and comparison with lysozyme
folding intermediates, Biochemistry, 36, 14375-14383.
82.Panick, G., Vidugiris, G. J., Malessa, R., Rapp,
G., Winter, R., and Royer, C. A. (1999) Exploring the
temperature-pressure phase diagram of staphylococcal nuclease,
Biochemistry, 38, 4157-4164.
83.Meersman, F., Smeller, L., and Heremans, K.
(2002) Comparative Fourier transform infrared spectroscopy study of
cold-, pressure-, and heat-induced unfolding and aggregation of
myoglobin, Biophys. J., 82, 2635-2644.
84.Bowron, D. T., Weigel, R., Filipponi, A.,
Roberts, M. A., and Finney, J. L. (2001) X-Ray absorption spectroscopy
investigations of the hydrophobic hydration of krypton at high
pressure, Mol. Phys., 99, 761-765.
85.Potekhin, S. A., Senin, A. A., Abdurachmanov, N.
N., and Tiktopulo, E. I. (2009) High-pressure stabilization of collagen
structure, Biochim. Biophys. Acta, 1794, 1151-1158.
86.Shoulders, M. D., and Raines, R. T. (2009)
Collagen structure and stability, Annu. Rev. Biochem.,
78, 929-958.
87.Finkelstein, A. V., and Shakhnovich, E. I. (1989)
Theory of cooperative transitions in protein molecules. II. Phase
diagram for protein molecule in solution, Biopolymers,
28, 1681-1694.